迟滞比较器计算公式与回差计算

　　迟滞比较器又可理解为加正反馈的单限比较器。单限比较器，如果输入信号Uin在门限值附近有微小的干扰，则输出电压就会产生相应的抖动（起伏）。在电路中引入正反馈可以克服这一缺点。

　　迟滞比较器电路组成

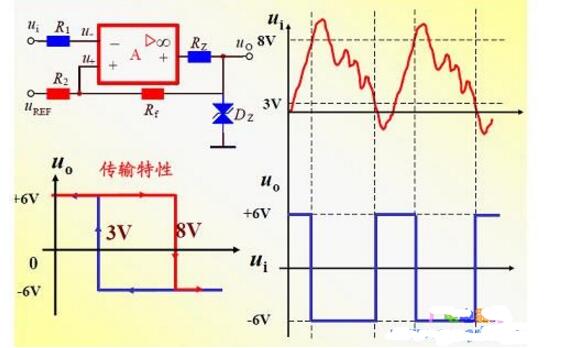
　　迟滞比较器是一个具有迟滞回环特性的比较器。图XX_02a所示为反相输入迟滞比较器原理电路，它是在反相输入单门限电压比较器的基础上引入了正反馈网络，其传输特性如图XX_02b所示。如将vI与VREF位置互换，就可组成同相输入迟滞比较器。

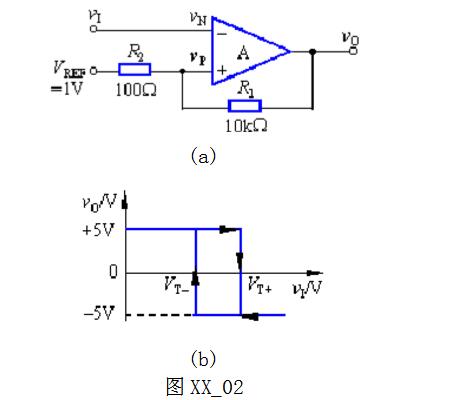
　　迟滞比较器电路

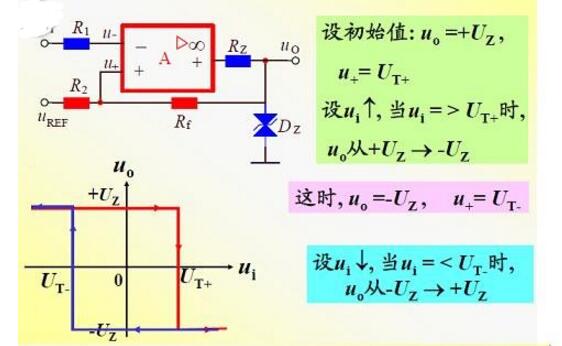
　　图1a给出了一个迟滞比较器，人们所熟悉的“史密特”电路即是有迟滞的比较器。图1b为迟滞比较器的传输特性。

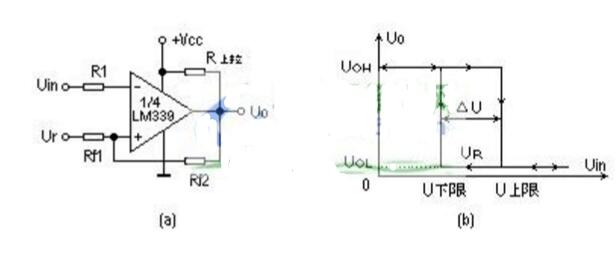
　　不难看出，当输出状态一旦转换后，只要在跳变电压值附近的干扰不超过ΔU之值，输出电压的值就将是稳定的。但随之而来的是分辨率降低。因为对迟滞比较器来说，它不能分辨差别小于ΔU的两个输入电压值。迟滞比较器加有正反馈可以加快比较器的响应速度，这是它的一个优点。除此之外，由于迟滞比较器加的正反馈很强，远比电路中的寄生耦合强得多，故迟滞比较器还可免除由于电路寄生耦合而产生的自激振荡。

　　迟滞比较器的计算公式

　　迟滞比较器的输出VO与输入VI不成线性关系，输出电压的转换临界条件是

　　门限电压VP（同相输入端的电压）≈VN（反相输入端的电压）=VI（参考基准电压）

　　VP=VN=［（R1×VREF）/（R1+R2）］+［（R2×VO）/（R1+R2）］（公式-1）

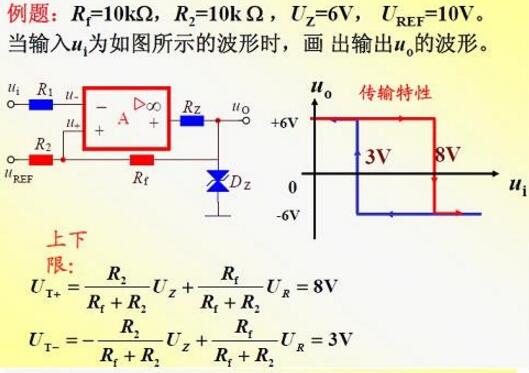
　　根据输出电压VO的不同值（VOH或VOL）可以分别求出上门限电压VT+和下门限电压VT-分别为：

　　VT+={［1+（R1/R2）］×VREF}-［（R1/R2）×VOL］（公式-2）

　　VT-={［1+（R1/R2）］×VREF}-［（R1/R2）×VOH］（公式-3）

　　那么门限宽度为：

　　ΔVT=（R1/R2）×（VOH-VOL）（公式-4）

　　例如：

　　已知工作电压=12V

　　基准电压VREF=1V

　　输入电压VI=1～5V

　　R1=1000Ω=1KΩR2=1000000Ω=1MΩ

　　反馈系数=R1/（R1+R2）=0.000999

　　比较器输出电压VOH=12V，VOL=0V

　　而比较器的门限宽度/输出电压=反馈系数

　　即反馈系数×输出电压=门限宽度

　　0.000999×12=0.011988≈0.012V

　　根据（公式-2）VT+={［1+（R1/R2）］×VREF}-［（R1/R2）×VOL］

　　={［1+（1000/1000000）］×1}-［（1000/1000000）×0］

　　=1.001-0

　　=1.001（V）

　　根据（公式3）VT-={［1+（R1/R2）］×VREF}-［（R1/R2）×VOH］

　　={［1+（1000/1000000）］×1}-［（1000/1000000）×12］

　　=1.001-0.012

　　=0.989（V）

　　根据（公式-4）ΔVT=（R1/R2）×（VOH-VOL）

　　=（1000/1000000）×12

　　=0.012（V）

　　验证VT+-VT-=1.001-0.989=0.012（V）

　　可以通过改变R2达到改变反馈系数来调节ΔVT的范围。

　　例如将R2改为10KΩ时，则

　　ΔVT=（R1/R2）×（VOH-VOL）

　　=（1000/10000）×12

　　=1.2（V）

　　例如将R2改为100KΩ时，则

　　ΔVT=（R1/R2）×（VOH-VOL）

　　=（1000/100000）×12

　　=0.12（V）

　　迟滞比较器计算

　　迟滞比较器的电路图如图6.3所示。该比较器是一个具有迟滞回环传输特性的比较器。由于正反馈作用，这种比较器的门限电压是随输出电压V0的变化而变化。在实际电路中为了满足负载的需要，通常在集成运放的输出端加稳压管限幅电路，从而获得合适的Voh和Vol。

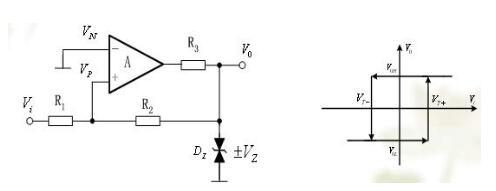
　　图6.3迟滞比较器图    6.4迟滞比较器电压传输特性

　　由图6.3可知：

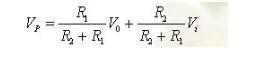
　　电路翻转时：

　　迟滞比较器的回差计算

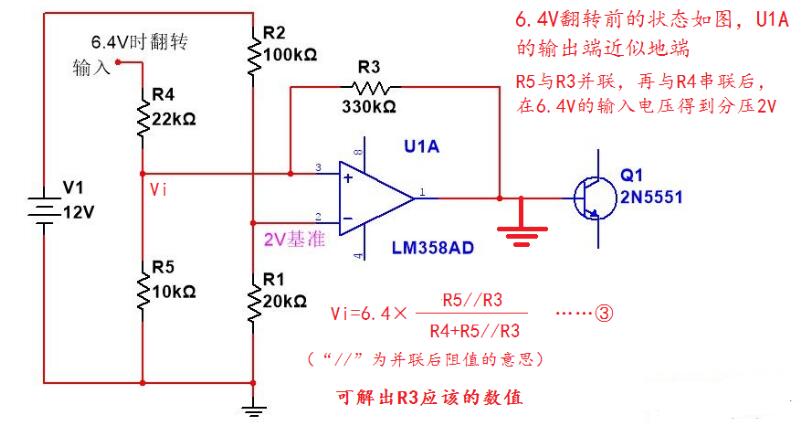
　　忽略运放的饱和压降，6.4V正翻转前，运放输出端等于接地，状态见图1，要反翻转，利用方程③，即可求出应该的R3数值。

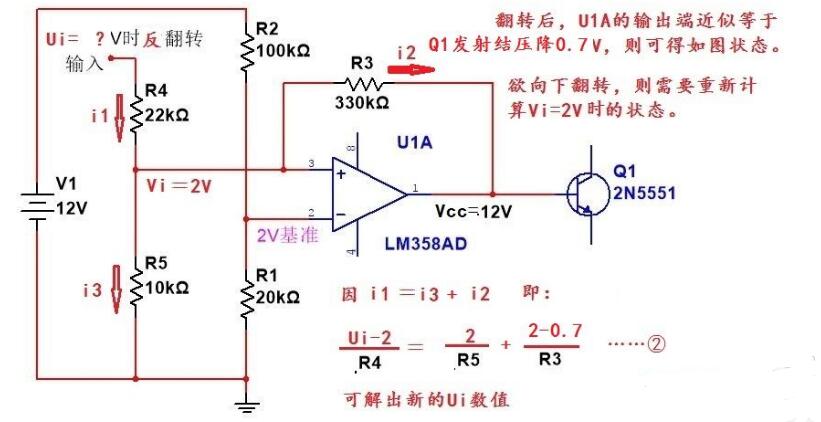
　　当反翻转前，运放输出端等于等于Q1的发射结饱和压降（设为0.7V），状态见图2，要反翻转，利用方程②，则反翻转输入信号电压Ui的值可计算出，这个值与6.4V有回差。但是不一定是1V。

　　如果要求回差等于1V，则计算较为复杂，不仅仅涉及到R3，还要涉及到R4或者R5的值，公式如下：

　　新设反翻转电压Ui=5.4……①

　　再设定R4或者R5中任意一个的数值，将方程①代入原来的方程②中，得到

　　（5.4-2）/R4=2/R5+（2-0.7）/R3……②

　　Vi=2=6.4×（R5//R3）/（R4+R5//R3）……③

　　以上两式组成二元方程组，这个方程组中，仅有两个未知数R3、R4（或R5）。解出这个方程组，就能得到当回差等于1V时，对应的R3、R4（或R5）应该的数值。

　　迟滞比较器电压传输特性