sift算法原理详解及应用

　一、Sift算法简介

　　Sift算法是David Lowe于1999年提出的局部特征描述子，并于2004年进行了更深入的发展和完善。Sift特征匹配算法可以处理两幅图像之间发生平移、旋转、仿射变换情况下的匹配问题，具有很强的匹配能力。总体来说，Sift算子具有以下特性：

　　（1）Sift特征是图像的局部特征，对平移、旋转、尺度缩放、亮度变化、遮挡和噪声等具有良好的不变性，对视觉变化、仿射变换也保持一定程度的稳定性。

　　（2）独特性好，信息量丰富，适用于在海量特征数据库中进行快速、准确的匹配。

　　（3）多量性，即使少数的几个物体也可以产生大量Sift特征向量。

　　（4）速度相对较快，经优化的Sift匹配算法甚至可以达到实时的要求。

　　（5）可扩展性强，可以很方便的与其他形式的特征向量进行联合。

　　其Sift算法的三大工序为：

　　（1）提取关键点；

　　（2）对关键点附加详细的信息（局部特征）也就是所谓的描述器；

　　（3）通过两方特征点（附带上特征向量的关键点）的两两比较找出相互匹配的若干对特征点，也就建立了景物间的对应关系。提取关键点和对关键点附加详细的信息（局部特征）也就是所谓的描述器可以称做是Sift特征的生成，即从多幅图像中提取对尺度缩放、旋转、亮度变化无关的特征向量。

　　Sift特征的生成一般包括以下几个步骤：

　　（1）构建尺度空间，检测极值点，获得尺度不变性；

　　

　　（2）特征点过滤并进行精确定位；

　　

　　（3）为特征点分配方向值；

　　

　　（4）计算变换参数

　　当两幅图像的Sift特征向量生成以后，下一步就可以采用关键点特征向量的欧式距离来作为两幅图像中关键点的相似性判定度量。取图1的某个关键点，通过遍 历找到图像2中的距离最近的两个关键点。在这两个关键点中，如果次近距离除以最近距离小于某个阙值，则判定为一对匹配点。

　　二、Surf算法原理

　　（1）构建Hessian矩阵

　　Hessian矩阵是Surf算法的核心，为了方便运算，假设函数f（z，y），Hessian矩阵H是由函数，偏导数组成：

　　

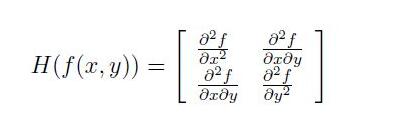
　　H矩阵判别式为：

　　

　　判别式的值是H矩阵的特征值，可以利用判定结果的符号将所有点分类，根据判别式取值正负，来判别该点是或不是极值点。在SURF算法中，用图像像素l（x，y）代替函数值f（x，y），选用二阶标准高斯函数作为滤波器，通过特定核间的卷积计算二阶偏导数，这样便能计算出H矩阵的三个矩阵元素L。、L。、k，从而计算出H矩阵：

　　

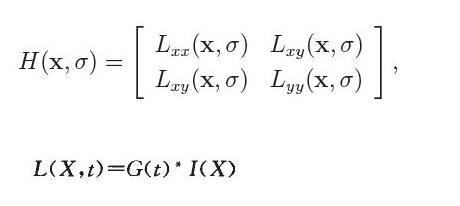
　　L。（X，￡）是一幅图像在不同解析度下的表示，可以利用高斯核G（￡）与图像函数，（X）在点X一（z，y）的卷积来实现，核函数G（￡）具体表示如式（5），g（￡）为高斯函数，t为高斯方差，L。与L。同理。通过这种方法可以为图像中每个像素计算出其H行列式的决定值，并用这个值来判别特征点。为方便应用，Herbert Bay提出用近似值现代替L。为平衡准确值与近似值间的误差引入权值叫，权值硼随尺度变化，则H矩阵判别式可表示为：

　　

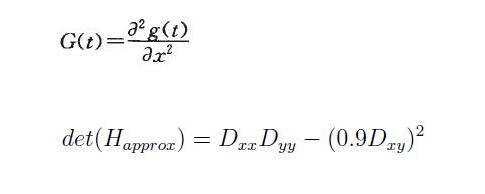
　　（2）构建尺度空间

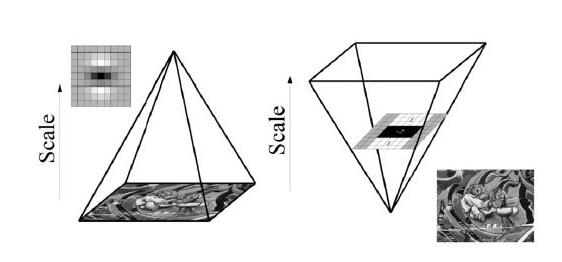
　　图像的尺度空间是这幅图像在不同解析度下的表示，由式（4）知，一幅图像j（X）在不同解析度下的表示可以利用高斯核G（￡）的卷积来实现，图像的尺度大小一般用高斯标准差来表示［6］。在计算视觉领域，尺度空间被象征性的表述为一个图像金字塔，其中，输入图像函数反复与高斯函数的核卷积并反复对其进行二次抽样，这种方法主要用于Sift算法的实现，但每层图像依赖于前一层图像，并且图像需要重设尺寸，因此，这种计算方法运算量较大，而SURF算法申请增加图像核的尺寸，这也是SIFT算法与SURF算法在使用金字塔原理方面的不同。算法允许尺度空间多层图像同时被处理，不需对图像进行二次抽样，从而提高算法性能。图1（a）是传统方式建立一个如图所示的金字塔结构，图像的寸是变化的，并且运（1） 算会反复使用高斯函数对子层进行平滑处理，图1（b）说明Surf算法使原始图像保持不变而只改变滤波器大小。

　　

　　（3）精确定位特征点

　　所有小于预设极值的取值都被丢弃，增加极值使检测到的特征点数量减少，最终只有几个特征最强点会被检测出来。检测过程中使用与该尺度层图像解析度相对应大小的滤波器进行检测，以3×3的滤波器为例，该尺度层图像中9个像素点之一图2检测特征点与自身尺度层中其余8个点和在其之上及之下的两个尺度层9个点进行比较，共26个点，图2中标记‘x’的像素点的特征值若大于周围像素则可确定该点为该区域的特征点。

　　

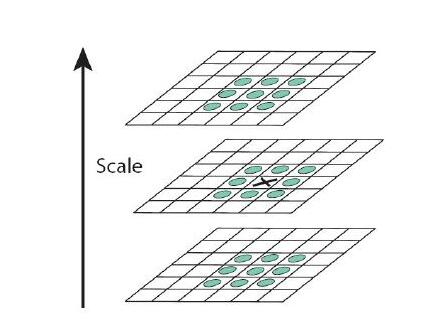
　　（4）主方向确定

　　为保证旋转不变性［8I，首先以特征点为中心，计算半径为6s（S为特征点所在的尺度值）的邻域内的点在z、y方向的Haar小波（Haar小波边长取4s）响应，并给这些响应值赋高斯权重系数，使得靠近特征点的响应贡献大，而远离特征点的响应贡献小，其次将60。范围内的响应相加以形成新的矢量，遍历整个圆形区域，选择最长矢量的方向为该特征点的主方向。这样，通过特征点逐个进行计算，得到每一个特征点的主方向。

　　

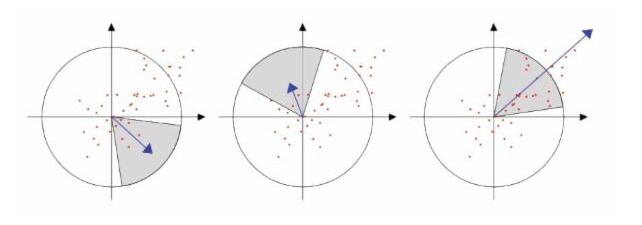
　　（5）特征点描述子生成

　　首先将坐标轴旋转为关键点的方向，以确保旋转不变性。

　　

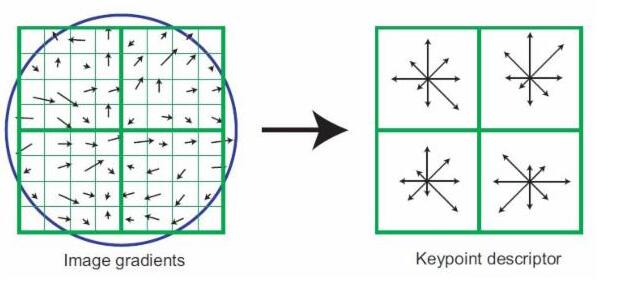
　　接下来以关键点为中心取8×8的窗口。图左部分的中央黑点为当前关键点的位置，每个小格代表关键点邻域所在尺度空间的一个像素，利用公式求得每个像素的梯度幅值与梯度方向，箭头方向代表该像素的梯度方向，箭头长度代表梯度模值，然后用高斯窗口对其进行加权运算，每个像素对应一个向量，长度为，为该像素点的高斯权值，方向为， 图中蓝色的圈代表高斯加权的范围（越靠近关键点的像素梯度方向信息贡献越大）。然后在每4×4的小块上计算8个方向的梯度方向直方图，绘制每个梯度方向的累加值，即可形成一个种子点，如图右部分示。此图中一个关键点由2×2共4个种子点组成，每个种子点有8个方向向量信息。这种邻域方向性信息联合的思想增强了算法抗噪声的能力，同时对于含有定位误差的特征匹配也提供了较好的容错性。

　　3、原理结束语

　　Sift/Surf采用Henssian矩阵获取图像局部最值还是十分稳定的，但是在求主方向阶段太过于依赖局部区域像素的梯度方向，有可能使得找到的主 方向不准确，后面的特征向量提取以及匹配都严重依赖于主方向，即使不大偏差角度也可以造成后面特征匹配的放大误差，从而匹配不成功；另外图像金字塔的层取 得不足够紧密也会使得尺度有误差，后面的特征向量提取同样依赖相应的尺度，发明者在这个问题上的折中解决方法是取适量的层然后进行插值。Sift是一种只 利用到灰度性质的算法，忽略了色彩信息，后面又出现了几种据说比Surf更稳定的描述器其中一些利用到了色彩信息，让我们拭目以待吧。

　　三、sift算法的应用

　　SIFT算法目前在军事、工业和民用方面都得到了不同程度的应用，其应用已经渗透了很多领域，典型的应用如下：

　　1、物体识别

　　

　　2、机器人定位与导航

　　3、图像拼接

　　

　　4、三维建模

　　

　　5、手势识别

　　

　　6、视频跟踪

　　7、笔记鉴定

　　

　　8、指纹与人脸识别

　　9、犯罪现场特征提取