

Teledyne Lecroy示波器插值算法
描述
示波器是通过内部硬件ADC对模拟信号采样来获取离散的数据点,然而这些离散的数据点有时难以完整呈现出原始模拟信号的全貌。软件插值算法的意义就在于,它能够依据特定的数学算法,在已采集的数据点之间插入新的数据点,帮助使用者更好地还原和分析模拟信号的波形。最普遍的插值算法有线性插值和正弦插值两种方式。
1线性插值
线性插值是示波器插值算法中最为简易的一种方式,它的计算量相对较小。其基本原理是在 硬件采样的原始相邻采样数据点之间依照线性多项式的计算方式插入一个计算值,插入的这个点为相邻两个采样点连线上的值。也就是说,它是假设用一条直线来连接每两个波形采样点。
线性插值的过程可以看作一个三角窗和原始波形的卷积。如图1所示,三角窗高度为1,宽度为两倍的采样周期。随着三角窗向右滑动,三角窗口和直线连接点的交点是插值点,可以用原始采样点和三角窗上对应点相乘相加得到。
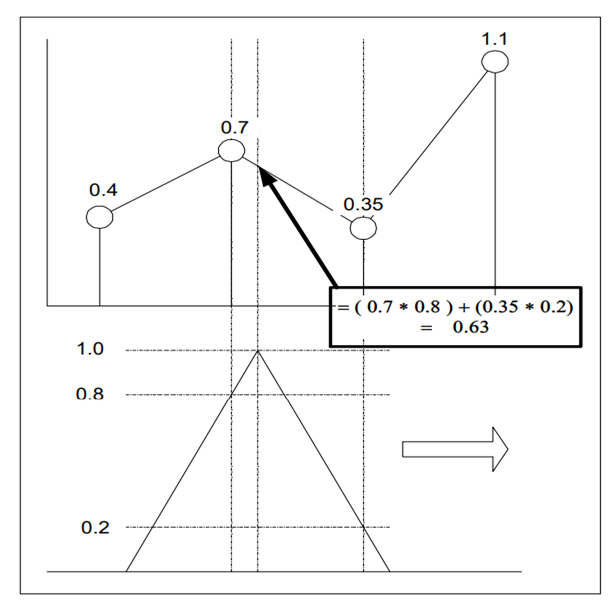
图1
例如,在实际的示波器单次捕获测试中,以点显示时,相邻两个采样点之间按照相应的线性关系插入新的点,从细节上看,能够看到类似于锯齿波的形状,如图2所示。通过线性插值来还原模拟波形从严格的数学意义来说是无效的,因为它的假设是波形两点是通过直线连接的,这在带宽有限的示波器中是不可能的,只能是在很大程度上是有效的。

图2
力科示波器的默认设置是不对原始硬件采样点进行插值,仅仅用直线将原始采样点连接起来,如图2所示。图3中Interpolation默认是None(Linear),力科示波器的设计原则是在不知道输入模拟信号的完整波形前提下,以真实的硬件采样点为准则,即使插值算法会使波形看起来更“漂亮”。

图3
力科示波器中display设置也可以将 “连直线” 显示波形改成以点的形式展示,如图4和图5所示。

图4

图5
2正弦插值
正弦插值是利用Sinc(Sinx/x)窗函数进行插值,如图6所示。它的原理是基于数字信号理论中奈奎斯特定理,即在模数转换时,模拟信号的最高频率小于采样率的二分之一。在满足奈奎斯特定理的前提下,用Sinc函数对采样后的数字信号进行卷积,就能无失真的表征原始模拟信号,也就是进行了信号重建。
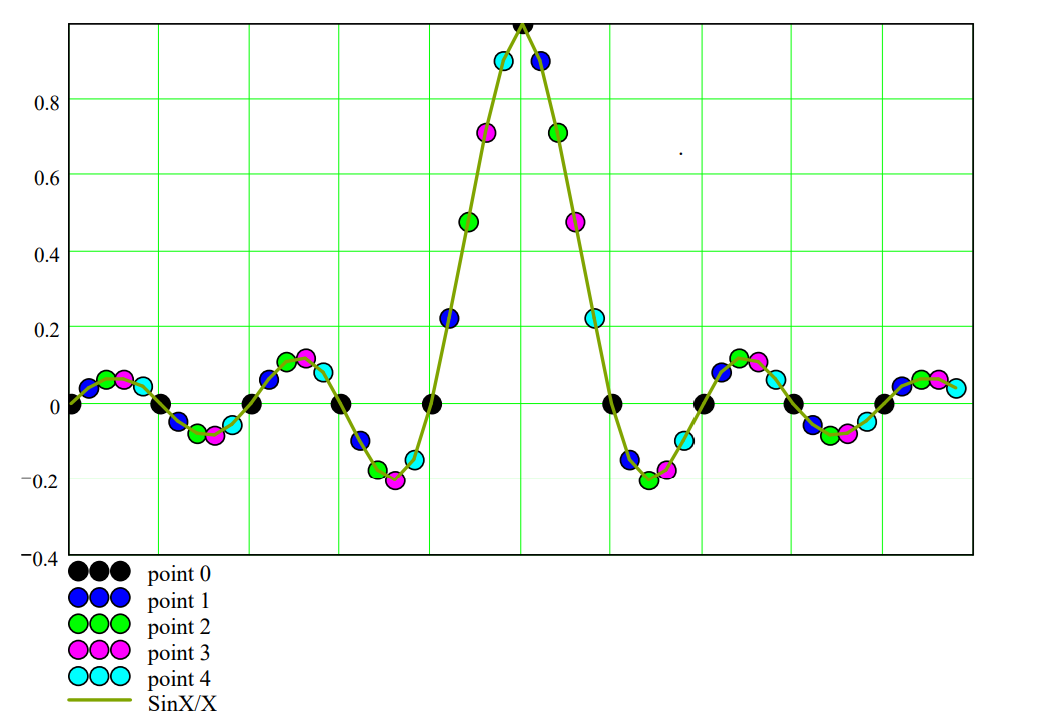
图6
这个方式从理论上看起来是完美的,适用于满足奈奎斯特定理的不同波形。但是在实践中,存在一些缺点。首先在理论中Sinc窗函数必须是无限长才能完美还原,但是实践中必须要进行截断,随之就会产生截断误差。另一方面,示波器硬件体系架构中不可避免的噪声和失真可能会超过奈奎斯特门限。
力科示波器的正弦插值同样可以在通道选项中进行设置,如图7所示,代表两倍上采样。

图7
3插值算法的适用性
插值算法使得数字信号更接近模拟信号的前提是示波器硬件采样率相对信号带宽足够大。一般来说,线性插值“有效”的前提条件是硬件采样率是信号最高频率(带宽)的10倍及以上;正弦插值“有效”的前提条件是硬件采样率是信号最高频率(带宽)的3倍到5倍。用户可以在设置足够大的采样率后,进行插值操作。
关于我们
特励达力科(Teledyne Lecroy)是高端示波器、协议分析仪和其他测试仪器的专业制造商,可快速全面地验证电子系统的性能和合规性,并进行复杂的调试分析。
1964 年成立以来,公司一直专注于将强大的工具整合到创新产品中,以提高“洞察时间”。更快的洞察时间使用户能够快速查找和修复复杂电子系统中的缺陷,从而显著缩短产品的上市时间。
-
基于插值A算法的路径规划2010-03-03 780
-
一种改进的线性图像插值算法2012-08-20 1492
-
基于LabVIEW的心电信号插值算法分析2013-03-15 1714
-
Teledyne LeCroy 发布电机驱动分析仪2015-02-09 1541
-
CCD图像的颜色插值算法研究及其FPGA实现2016-08-29 592
-
多项式插值算法框架2018-01-05 836
-
实时图像插值算法2018-01-17 489
-
Teledyne LeCroy发布2个高分辨技术的示波器2018-04-24 5076
-
LeCroy第四代示波器:世界工程的影响者(中)2018-06-22 4543
-
常用的插值算法盘点2019-01-01 8918
-
分形插值算法的详细资料说明2019-06-05 974
-
Python插值算法基本的概念2022-07-12 1903
-
Teledyne收购Xena Networks 扩展Teledyne LeCroy的协议测试产品2023-10-11 1663
-
Teledyne LeCroy扩展CrossSync PHY技术到PCI Express 6.02024-02-23 1185
-
LeCroy力科HDO4024示波器开机报错维修案例2024-12-19 1173
全部0条评论

快来发表一下你的评论吧 !

