

如何画卡诺图_卡诺图化简约束条件
电子常识
描述
一、什么是卡诺图
卡诺图是逻辑函数的一种图形表示。一个逻辑函数的卡诺图就是将此函数的最小项表达式中的各最小项相应地填入一个方格图内,此方格图称为卡诺图。
卡诺图的构造特点使卡诺图具有一个重要性质:可以从图形上直观地找出相邻最小项。两个相邻最小项可以合并为一个与项并消去一个变量。
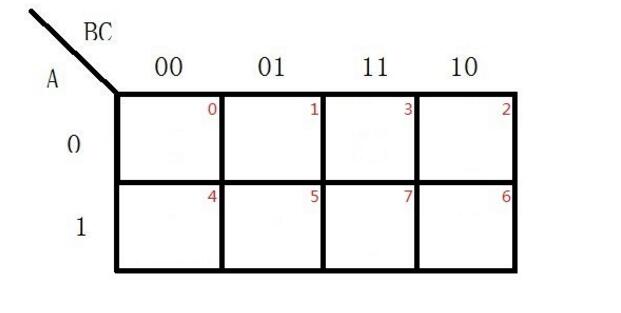
二、卡诺图结构特点
卡诺图中最小项的排列方案不是唯一的,变量的坐标值0表示相应变量的反变量,1表示相应变量的原变量,变量的取值变化规律按“循环码”变化。各小方格依变量顺序取坐标值,所得二进制数对应的十进制数即相应最小项的下标i。
在五变量卡诺图中,为了方便省略了符号“m”,直接标出m的下标i。
归纳起来,卡诺图在构造上具有以下两个特点:
☆n个变量的卡诺图由2^n个小方格组成,每个小方格代表一个最小项;
☆卡诺图上处在相邻、相对、相重位置的小方格所代表的最小项为相邻最小项。
可以从图形上直观地找出相邻最小项。两个相邻最小项可以合并为一个与项并消去一个变量。
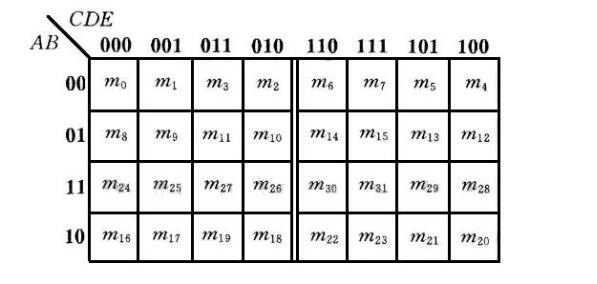
三、卡诺图的性质
卡诺图的构造特点使卡诺图具有一个重要性质:可以从图形上直观地找出相邻最小项合并。合并的理论依据是并项定理AB+AB=A。例如,
根据定理AB+AB=A和相邻最小项的定义,两个相邻最小项可以合并为一个与项并消去一个变量。例如,4变量最小项ABCD和ABCD相邻,可以合并为ABD;ABCD和ABCD相邻,可以合并为ABD;而与项ABD和ABD又为相邻与项,故按同样道理可进一步将两个相邻与项合并为BD。
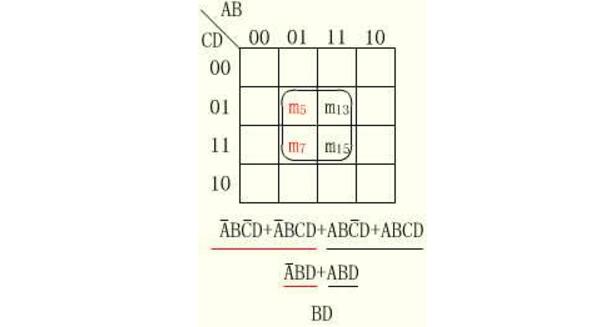
用卡诺图化简逻辑函数的基本原理就是把上述逻辑依据和图形特征结合起来,通过把卡诺图上表征相邻最小项的相邻小方格“圈”在一起进行合并,达到用一个简单“与”项代替若干最小项的目的。
通常把用来包围那些能由一个简单“与”项代替的若干最小项的“圈”称为卡诺圈。
四、画卡诺图方法及步骤
第一步:将逻辑函数变换为最小项之和的形式
第二步:画出表示该逻辑函数的卡诺图
第三步:找出可以合并的最小项并画出合并圈
第四步:写出最简的与-或表达式
在利用卡诺图化简逻辑函数时,关键在于画合并圈。合并圈画得不同,逻辑函数的表达式也不相同。因此画合并圈时应注意以下几点:
①首先要找出孤立的1方格并画圈。
②合并圈的范围越大越好,但必须包含(i=0,1,2,3…)个1方格,这样能消去的变量就越多。
③合并圈的个数越少越好,因为合并圈的个数与化简结果中乘积项的个数相对应,圈数越少意味着与-或表达式中与项越少。
④每个合并圈中至少要包含一个其它合并圈中没有包含的1方格,这样才能保证这个合并圈不是多余的。
⑤卡诺图中所有的1方格至少要被圈一次,不能有漏画的1方格。
这样,把每个合并圈相对应的与项“加”起来,就得到最简的与-或表达式。
同理的方法,只要合并圈改为针对卡诺图中的0方格进行,找出可合并的最大项,就可得到逻辑函数的最简或-与表达式。
合并最大项的规律与合并最小项的规律基本一致。不同之处在于,合并最大项时必须找出0方格的相邻性。每个合并圈可由(i=0,1,2,3…)个0方格构成,每个合并圈对应于一个或项,该或项由圈内取值不变的变量相或来构成,其中取值为0的对应原变量,取值为1的对应反变量。然后将每个合并圈对应的或项进行相与,便得到最简的或-与表达式。
五、卡诺图化简约束条件
用卡诺图法将下列具有约束条件的逻辑函数化简成为最简“与-或”表达式。即
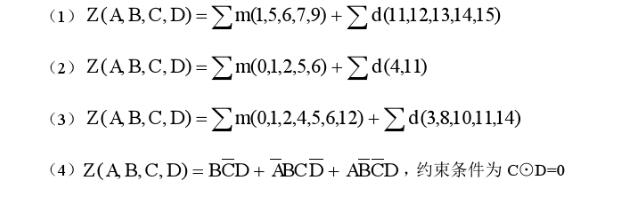
-
 电子科技宅
2018-11-24
0 回复 举报谢谢大佬的分享 收起回复
电子科技宅
2018-11-24
0 回复 举报谢谢大佬的分享 收起回复
- 相关推荐
- 热点推荐
- 卡诺图
-
卡诺图如何化简2022-11-01 6550
-
卡诺图化简画圈的原则和步骤2020-03-06 141888
-
数字逻辑基础卡诺图化简2019-05-30 3902
-
卡诺图化简法例题详解2018-03-07 331788
-
卡诺图简化方法及简化步骤介绍2018-03-01 60439
-
卡诺图化简逻辑函数.ppt2015-10-29 1286
-
带约束条件的函数化简2010-09-19 10579
-
次态卡诺图在时序逻辑电路中的应用2010-05-25 1031
-
卡诺图,卡诺图是什么意思2010-03-08 13273
-
第五讲 逻辑函数的卡诺图化简法2009-03-30 6523
-
卡诺图化简法2008-09-27 2255
-
逻辑函数的卡诺图化简法2008-01-21 823
全部0条评论

快来发表一下你的评论吧 !

