逻辑异或运算怎么算

　　逻辑异或运算简介

　　逻辑异或运算简称异或。异或，英文为exclusiveOR，缩写成xo。异或（xor）是一个数学运算符。它应用于逻辑运算。异或的数学符号为“⊕”，计算机符号为“xor”。其运算法则为：

　　a⊕b=（¬a∧b）∨（a∧¬b）

　　如果a、b两个值不相同，则异或结果为1。如果a、b两个值相同，异或结果为0。

　　异或也叫半加运算，其运算法则相当于不带进位的二进制加法：二进制下用1表示真，0表示假，则异或的运算法则为：0⊕0=0，1⊕0=1，0⊕1=1，1⊕1=0（同为0，异为1），这些法则与加法是相同的，只是不带进位。

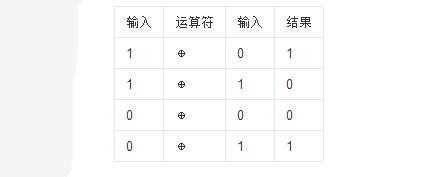
　　逻辑异或运算性质

　　1、交换律

　　2、结合律（即（a^b）^c==a^（b^c））

　　3、对于任何数x，都有x^x=0，x^0=x

　　4、自反性AXORBXORB=Axor0=A

　　异或运算最常见于多项式除法，不过它最重要的性质还是自反性：AXORBXORB=A，即对给定的数A，用同样的运算因子（B）作两次异或运算后仍得到A本身。这是一个神奇的性质，利用这个性质，可以获得许多有趣的应用。例如，所有的程序教科书都会向初学者指出，要交换两个变量的值，必须要引入一个中间变量。但如果使用异或，就可以节约一个变量的存储空间：设有A，B两个变量，存储的值分别为a，b，则以下三行表达式将互换他们的值表达式（值）：

　　A=AXORB（aXORb）

　　B=BXORA（bXORaXORb=a）

　　A=AXORB（aXORbXORa=b）

　　类似地，该运算还可以应用在加密，数据传输，校验等等许多领域。

　　逻辑异或运算怎么算

　　逻辑异或运算简称异或。英文为exclusiveOR，或缩写成xor。

　　异或（xor）是一个数学运算符。它应用于逻辑运算。异或的数学符号为“⊕”，计算机符号为“xor”。其运算法则为：

　　a⊕b=（¬a∧b）∨（a∧¬b）

　　如果a、b两个值不相同，则异或结果为1。如果a、b两个值相同，异或结果为0。

　　异或逻辑

　　逻辑表达式：F=AB’⊕A’B（（AB’⊕A’B）’=AB⊙A’B’，⊙为“同或”运算）

　　异或逻辑的真值表如图1所示

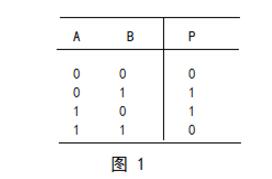
　　示，其逻辑符号如图2所示。异或逻辑的关系是：当AB不同时，输出P=1；当AB相同时，输出P=0。“⊕”是异或运算符号，异或逻辑也是与或非逻辑的组合，其逻辑表达式为：

　　P=A⊕B

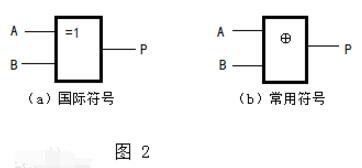
　　由图1可知，异或运算的规则是

　　0⊕0=0，0⊕1=1

　　1⊕0=1，1⊕1=0

　　口诀：相同取0，相异取1

　　事实上，XOR在英文里面的定义为eitherone（isone），butnotboth，也即只有一个为真（1）时，取真（1）。

　　逻辑异或运算应用

　　1-1000放在含有1001个元素的数组中，只有唯一的一个元素值重复，其它均只出现一次。每个数组元素只能访问一次，设计一个算法，将它找出来；不用辅助存储空间，能否设计一个算法实现？

　　解法一、显然已经有人提出了一个比较精彩的解法，将所有数加起来，减去1+2+.。.+1000的和。

　　这个算法已经足够完美了，相信出题者的标准答案也就是这个算法，唯一的问题是，如果数列过大，则可能会导致溢出。

　　解法二、异或就没有这个问题，并且性能更好。

　　将所有的数全部异或，得到的结果与1^2^3^.。.^1000的结果进行异或，得到的结果就是重复数。

　　但是这个算法虽然很简单，但证明起来并不是一件容易的事情。这与异或运算的几个特性有关系。

　　首先是异或运算满足交换律、结合律。

　　所以，1^2^.。.^n^.。.^n^.。.^1000，无论这两个n出现在什么位置，都可以转换成为1^2^.。.^1000^（n^n）的形式。

　　其次，对于任何数x，都有x^x=0，x^0=x。

　　所以1^2^.。.^n^.。.^n^.。.^1000 = 1^2^.。.^1000^（n^n）= 1^2^.。.^1000^0 = 1^2^.。.^1000（即序列中除了n的所有数的异或）。

　　令，1^2^.。.^1000（序列中不包含n）的结果为T

　　则1^2^.。.^1000（序列中包含n）的结果就是T^n。

　　T^（T^n）=n。

　　所以，将所有的数全部异或，得到的结果与1^2^3^.。.^1000的结果进行异或，得到的结果就是重复数。

　　当然有人会说，1+2+.。.+1000的结果有高斯定律可以快速计算，但实际上1^2^.。.^1000的结果也是有规律的，算法比高斯定律还该简单的多。

　　google面试题的变形：一个数组存放若干整数，一个数出现奇数次，其余数均出现偶数次，找出这个出现奇数次的数？

　　解法有很多，但是最好的和上面一样，就是把所有数异或，最后结构就是要找的，原理同上