

余3码至8421BCD码的转换_8421BCD码转换成余3码
电子说
描述
一:8421BCD码
二进制编码的十进制数,简称BCD码(Binarycoded Decimal)。这种方法是用4位二进制码的组合代表十进制数的0,1,2,3,4,5,6 ,7,8,9 十个数符。最常用的BCD码称为8421BCD码,8.4.2.1 分别是4位二进数的位取值。
将十进制数75.4转换为BCD码如:
75.4=(0111 0101.0100)BCD 若将BCD码1000 0101.0101转换为十进制数如: (1000 0101.0101)BCD=85.5
注意:同一个8位二进制代码表示的数,当认为它表示的是二进制数和认为它表示的是二进制编码的十进制数时,数值是不相同的。
例如:00011000,当把它视为二进制数时,其值为24;但作为2位BCD码时, 其值为18。
又例如00011100,(这表示8位的二进制数)如将其视为二进制数,其值为28,但不能当成BCD码,因为在8421BCD码中,它是个非法编码 。
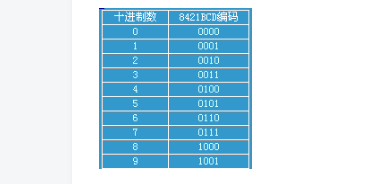
右图为十进制数和8421BCD编码的对应关系表:
二:余3码
由8421码加3后形成的余3码是一种BCD码,它是由8421码加3后形成的(即余3码是在8421码基础上每位十进制数BCD码再加上二进制数0011得到的)。因为8421码中无1010~1111这6个代码,所以余3码中无0000~0010、1101~1111这6个代码。余3码不具有有权性,但具有自补性,余3码是一种“对9的自补码”
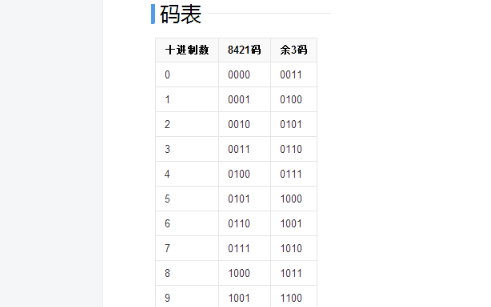
8421码是中国大陆的叫法,
即BCD代码。Binary-Coded Decimal,简称BCD,称BCD码或二-十进制代码,亦称二进码十进数。是一种二进制的数字编码形式,用二进制编码的十进制代码。这种编码形式利用了四个位元来储存一个十进制的数码,使二进制和十进制之间的转换得以快捷的进行。这种编码技巧,最常用于会计系统的设计里,因为会计制度经常需要对很长的数字串作准确的计算。相对于一般的浮点式记数法,采用BCD码,既可保存数值的精确度,又可免却使电脑作浮点运算时所耗费的时间。此外,对于其他需要高精确度的计算,BCD编码亦很常用。
由于十进制数共有0、1、2、……、9十个数码,因此,至少需要4位二进制码来表示1位十进制数。4位二进制码共有2^4=16种码组,在这16种代码中,可以任选10种来表示10个十进制数码,共有N=16!/(16-10)!约等于2.9乘以10的10次方种方案。常用的BCD代码列于末。
余3码至8421BCD码的转换
最常用的BCD编码,就是使用“0”至“9”这十个数值的二进码来表示。这种编码方式,在中国大陆称之为“8421码”。除此以外,对应不同需求,各人亦开发了不同的编码方法,以适应不同的需求。这些编码,大致可以分成有权码和无权码两种:
有权BCD码,如:8421(最常用)、2421、5421…
无权BCD码,如:余3码、格雷码…
余三码是一种对9的自补代码,因而可给运算带来方便。其次,在将两个余三码表示的十进制数相加时,能正确产生进位信号,但对“和”必须修正。修正的方法是:如果有进位,则结果加3;如果无进位,则结果减3。
8421BCD码转换成余3码
通过WEWB32软件实验,输入BCD码转换成余三码的逻辑函数为:
输入端口a,b,c,d,输出端口e,f,g,h,用G3,G2,G1,G0表示:
G3=A’BC+A’BD+ABC’
G2=A’B’C+A’BC’D’+B’C’D
G1=A’C’D’+A’CD+B’C’D’
G0=A’D’+B’C’D’
有逻辑函数画出逻辑电路图如下:
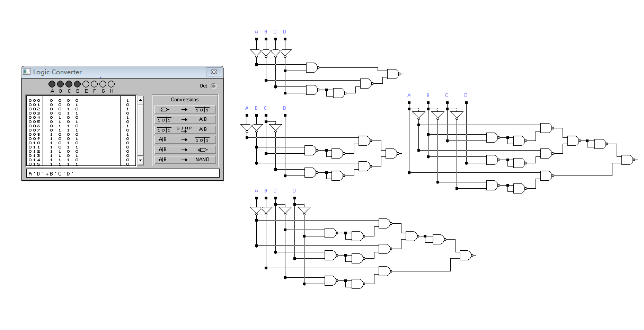
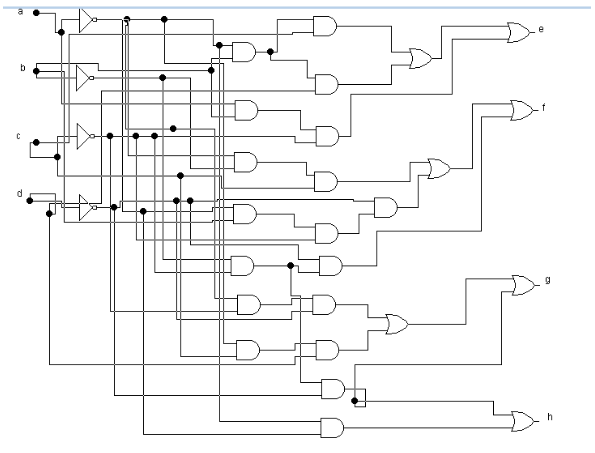
-
什么是BCD码2022-09-07 18158
-
在FPGA中实现一种二进制转BCD码的电路设计2022-07-12 4557
-
8421BCD码与二进制原码的相互转换2022-01-17 1840
-
C语言中十进制转8421BCD码是用的什么方法?2021-07-15 2383
-
8421码转换十进制程序2018-03-02 34948
-
关于两位十进制数转换成二进制数的仿真 求助啊2016-07-01 9085
-
什么是BCD码、8421码、余三码、格雷码2011-11-03 27711
-
常用编码(BCD编码、余3码、格雷反射码、奇偶校验码)2010-09-19 10631
-
二进制与BCD码转换资料2010-08-19 2502
-
双字节BCD码整数转换成双字节十六进制整2009-01-19 3189
全部0条评论

快来发表一下你的评论吧 !

