8421bcd码运算规则

BCD代码。Binary-Coded Decimal‎，简称BCD，称BCD码或二转十进制代码，亦称二进码十进数。是一种二进制的数字编码形式，用二进制编码的十进制代码。这种编码形式利用了四个位元来储存一个十进制的数码，使二进制和十进制之间的转换得以快捷的进行。这种编码技巧，最常用于会计系统的设计里，因为会计制度经常需要对很长的数字串作准确的计算。相对于一般的浮点式记数法，采用BCD码，既可保存数值的精确度，又可免却使电脑作浮点运算时所耗费的时间。此外，对于其他需要高精确度的计算，BCD编码亦很常用。

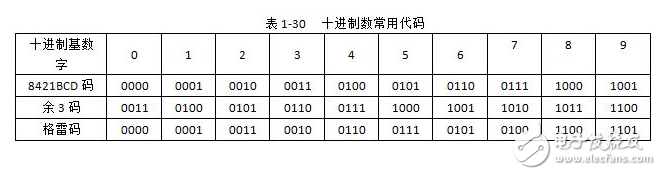
由于十进制数共有0、1、2、……、9十个数码，因此，至少需要4位二进制码来表示1位十进制数。4位二进制码共有2^4=16种码组，在这16种代码中，可以任选10种来表示10个十进制数码，共有N=16！/（16-10）！约等于2.9乘以10的10次方种方案。常用的BCD代码列于末。

BCD码的运算法则

BCD码的运算规则：BCD码是十进制数，而运算器对数据做加减运算时，都是按二进制运算规则进行处理的。这样，当将 BCD码传送给运算器进行运算时，其结果需要修正。

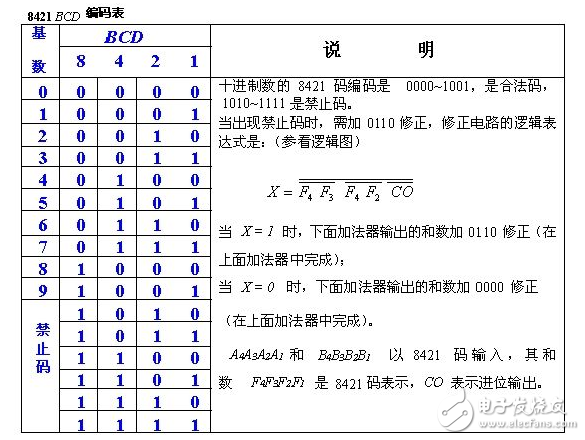
修正的规则是：当两个BCD码相加，如果和等于或小于 1001（即十进制数 9），不需要修正；如果相加之和在 1010 到1111（即十六进制数 0AH～0FH）之间，则需加 6 进行修正；如果相加时，本位产生了进位，也需加 6 进行修正。这样做的原因是，机器按二进制相加，所以 4 位二进制数相加时，是按“逢十六进一”的原则进行运算的，而实质上是 2 个十进制数相加，应该按“逢十进一”的原则相加，16 与10相差 6，所以当和超过 9或有进位时，都要加 6 进行修正。下面举例说明。

需要修正 BCD码运算值的举例。

（1） 计算 5+8；

（2） 计算 8+8

解：（1） 将 5 和 8 以 8421 BCD输入机器，则运算如下：

0 1 0 1

+） 1 0 0 0

1 1 0 1 结果大于 9

+） 0 1 1 0 加 6 修正

1 0 0 1 1 13 的 BCD码

结果是 0011，即十进制数 3，还产生了进位。5+8=13，结论正确。

（2）将8以8421 BCD输入机器，则运算如下：

1 0 0 0

+）1 0 0 0

1 0 0 0 0 结果大于9

+）0 1 1 0 加6修正

1 0 1 1 0 16的BCD码

结果是0110，即十进制的6，而且产生进位。8+8=16，结论正确。

微机原理代码： （AL=BCD 5，BL=BCD 8） 设AH=0，则

ADD AL，BL

AAA

结果为 AX=0104H，表示非压缩十进制数，CF=1，AF=1，AH=1，AL=1

使用AAA指令，可以不用屏蔽高半字节，只要在相加后立即执行AAA指令，便能在AX中得到一个正确的非压缩十进制数

压缩BCD码与非压缩BCD码的区别—— 压缩BCD码的每一位用4位二进制表示，一个字节表示两位十进制数。例如10010110B表示十进制数96D；非压缩BCD码用1个字节表示一位十进制数，高四位总是0000，低4位的0000~1001表示0~9.例如00001000B表示十进制数8.