

汉明码计算及其纠错原理详解
电子说
描述
当计算机存储或移动数据时,可能会产生数据位错误,这时可以利用汉明码来检测并纠错,简单的说,汉明码是一个错误校验码码集,由Bell 实验室的R.W.Hamming 发明,因此定名为汉明码。
汉明码(Hamming Code),是在电信领域的一种线性调试码,以发明者理查德·卫斯里·汉明的名字命名。汉明码在传输的消息流中插入验证码,以侦测并更正单一比特错误。由于汉明编码简单,它们被广泛应用于内存(RAM )。其SECDED (single error correction, double error detection)版本另外加入一检测比特,可以侦测两个或以下同时发生的比特错误,并能够更正单一比特的错误。因此,当发送端与接收端的比特样式的汉明距离(Hamming distance)小于或等于1时(仅有1 bit发生错误),可实现可靠的通信。相对的,简单的奇偶检验码除了不能纠正错误之外,也只能侦测出奇数个的错误。
在数学方面,汉明码是一种二元线性码。对于每一个整数,存在一个编码,带有个奇偶校验位个数据位。该奇偶检验矩阵的汉明码是通过列出所有米栏的长度是两两独立。
汉明码的定义和汉明码不等式:
设:m=数据位数,k=校验位数为,n=总编码位数=m+k,有Hamming不等式:
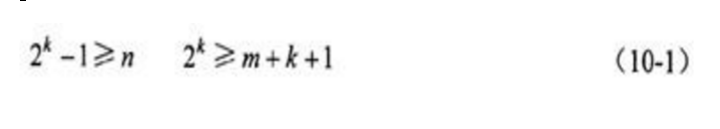
汉明码不等式含义:
a) 总数据长度为N,如果每一位数据是否错误都要记录,就需要N位来存储。
b) 每个校验位都可以表示:对或错;校验位共K位,共可表示2k种状态
c) 总编码长度为N,所以包含某一位错和全对共N+1种状态。
d) 所以2k≧N+1 e) 数据表见下
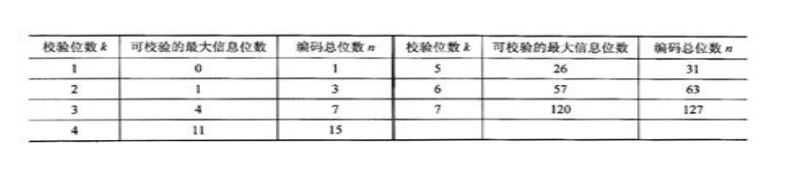
Hamming码缺点:
无法实现2位或2位以上的纠错,Hamming码只能实现一位纠错。
以典型的4位数据编码为例,演示汉明码的工作过程
a) 数据存储格式:

依照此前的汉明码不等式计算出,当数据位为4位时,汉明码校验位至少为3位,如上方式排列
可以看的出D8、D4、D2、D1中的数字都是2的整数幂
b) 汉明校验码的插入规律:
设:编码位代号k,校验码位代号p,数据位代号n
某个校验码Pp将处于整个编码的第k位
k=2^(p-1)=2的(p-1)次方
以数据位为5的一组9位数编码为例,如下:

c) 校验位与数据位的对应关系:
注:^是逻辑运算符异或。
P1=D8^D4^D1
P2=D8^D2^D1
P3=D4^D2^D1
小解释:数据位共4位每行等式都缺少一位,而缺少的这位数据位正好是DX,等式左边的校验位为PY,X=2y.
d) 校验位如何参与计算:
P1’=P1^D8^D4^D1
P2’=P2^D8^D2^D1
P3’=P3^D4^D2^D1
从高到低排列的二进制数:P3’ P2’ P1’表示的就是出错的编码位,从000-011-101-110-111共5种组合,可表示原数据位D8D4D2D1某一位错&没错的一共5种状态。
e) 设有一数字为:1101,带入运算:
D8=1、D4=1、D2=0、D1=1,
P1 =1,P2=0、P3=0。
汉明码处理的结果就是1010101
假设:D8出错,P3’ P2’ P1’=011=十进制的3,即表示编码后第三位出错,对照存储格式表,果然就是D8错误。
假设:D4错误,P3’ P2’ P1’=101=十进制的5,即表示编码后第五位出错,对照存储格式表,果然就是D4错误。
- 相关推荐
- 热点推荐
- 汉明码
-
请问汉明码(7,4)一共有多少种码字呢?2013-05-22 5714
-
基于FPGA的汉明码译码器如何对码元数据添加噪声干扰?2020-02-26 9428
-
【原创】基于FPGA的汉明码编码解码设计2020-04-15 3457
-
如何提高汉明码的纠错能力?2021-04-27 1466
-
提高汉明码对突发干扰的纠错能力2009-04-15 929
-
PIC单片机串行通信中的汉明编码自动检纠错2009-05-16 1340
-
一种基于汉明码和湿纸码的隐写算法2010-02-09 942
-
利用FPGA实现模式可变的卫星数据存储器纠错系统2009-06-20 734
-
汉明码,汉明码是什么意思2010-03-17 8742
-
基于FPGA的检纠错逻辑算法的实现2011-09-15 2018
-
MATLAB实现汉明码编码译码2018-03-02 14054
-
汉明码编译码器的数据手册免费下载2019-12-13 1107
-
汉明码纠错的基本原理及优化解决方案2020-09-16 16965
-
汉明码编译码文档2023-11-17 537
全部0条评论

快来发表一下你的评论吧 !

