汉明码编码原理介绍

为了保证通信过程中数据传输的正确性和完整性，并且在通信过程中，如果数据传输发生一位错误，能够将其矫正过来，将信息数据进行汉明编码后再进行数据传输。

汉明码（Hamming Code）也叫海明码，是Richard Hamming（贝尔实验室）于1950年发明的，汉明码也是利用了奇偶校验位概念，通过在数据位后增加一些比特以验证数据的有效性，故汉明码也属于线性纠错码（可纠错1-bit错误检出2-bit错误）。汉明码无法实现2位及2位以上纠错。

汉明码原理

汉明码运算需要构造G生成矩***和H监督矩***，关于构造方法可参考相关计算机原理书籍，这里只需了解些简单的概念即可。

设数据位数为m，校验位数为k，则总编码位数为n，所以，n＝m+k，则，

有Hamming不等式：

2^k-1》=n

也可表示为：2^k》=m+k+1，该不等式用于对比运算计算数据位数和检验位数，举个例子假设数据位为64，那么校验位则为（“2^k-k》=65” =》k=7）。

校验位数一般指最小值，因为k越小总信息位会越小，传输开销自然越小。

信息位数一般指最大值，但由于2^k-k只能在固定的离散值里取值，所以信息位也可能不是最大值，比如信息位为24，计算需要校验位5，但同样可信息位为25时，校验位同样是5。

校验位数VS信息位数关系如下表：

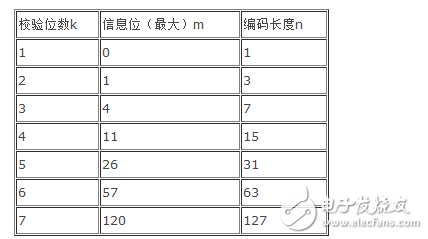
注：汉明码的特性决定，一般不会做太多信息位的校验，信息位越长出现多余两个错误的概率会越高，这将带来纠错的难度。

汉明码编码原理

设码长为n，信息位长度为k，监督位长度为r=n-k。如果需要纠正一位出错，因为长度为n的序列上每一位都可能出错，一共有n种情况，另外还有不出错的情况，所以我们必须用长度为r的监督码表示出n+1种情况。而长度为r的监督码一共可以表示2^r种情况 。因此

2^r 》= n + 1， 即r 》= log（n+1）

我们以一个例子来说明汉明码。假设k=4，需要纠正一位错误，则

2^r 》= n + 1 = k + r + 1 = 4 + r + 1

解得r 》= 3。我们取r=3，则码长为3+4=7。用a6，a5，。。.a0表示这7个码元。用S1，S2，S3表示三个监关系式中的校正子。我们作如下规定（这个规定是任意的）：

S1 S2 S3 错码的位置

0 0 1 a0

0 1 0 a1

1 0 0 a2

0 1 1 a3

1 0 1 a4

1 1 0 a5

1 1 1 a6

0 0 0 无错

按照表中的规定可知，仅当一个错码位置在a2，a4，a5或a6时校正子S1为1，否则S1为0。这就意味着a2，a4，a5，a6四个码元构成偶校验关系：

S1 = a6⊕a5⊕a4⊕a2 （1）式

同理，可以得到：

S2 = a6⊕a5⊕a3⊕a1 （2）式

S3 = a6⊕a4⊕a3⊕a0 （3）式

在发送信号时，信息位a6，a5，a4，a3的值取决于输入信号，是随机的。监督为a2，a1，a0应该根据信息位的取值按照监督关系决定，即监督位的取值应该使上述（1）（2）（3）式中的S1，S2，S3为0，这表示初始情况下没有错码。即

a6⊕a5⊕a4⊕a2 = 0

a6⊕a5⊕a3⊕a1 = 0

a6⊕a4⊕a3⊕a0 = 0

由上式进行移项运算，得到：

a2 = a6⊕a5⊕a4

a1 = a6⊕a5⊕a3

a0 = a6⊕a4⊕a3

已知信息位后，根据上式即可计算出a2，a1，a0三个监督位的值。

接收端受到每个码组后，先按照（1）~（3）式计算出S1，S2，S3，然后查表可知错码情况。

例如，若接收到的码字为0000011，按照（1）~（3）计算得到：

S1 = 0， S2 = 1， S3 = 1

查表可得在a3位有一个错码。

这种编码方法的最小汉明距离为d=3，所以这种编码可以纠正一个错码或者检测两个错码。

汉明码实例

下文示例为（30，24）汉明码计算方法，用在MIPI DSI包头部分（MIPI Alliance Specification for Display Serial Interface，Chapter 9），DSI包头格式固定为24bits Data+8bits ECC，8bitsECC中预设P6=P7=0，所以实际n=30，m=24，k=6。

检验位计算方法参考MIPI DSI table22生成矩***（Px vs ［DataBit0~DataBitx］），比如P5=D10^D11^.。。.D23，表示对应DataBit23的P5列，只有这些DataBit位为1。

int main（） {

char res;

char in［20］={0};

char D0，D1，D2，D3，D4，D5，D6，D7，D8，D9，D10，D11，D12，D13，D14，D15，D16，D17，D18，D19，D20，D21，D22，D23;

char P0，P1，P2，P3，P4，P5，P6，P7;

cout《《“Checking Codes（eg.0x1234AF， \”-\“ for exit）： 0x”;

cin》》in;

if（in［0］==‘-’） {

return 0;

}

for（int i=0;i《6;i++）{

if（（in［i］》=‘0’） && （in［i］《=‘9’）） {

in［i］ = in［i］-0x30;

}else if（（in［i］》=‘A’） && （in［i］《=‘F’））{

in［i］ = in［i］-‘A’+10;

}else {

return 0;

}

}

D0=in［1］&0x01; D1=（in［1］&0x02）》》1;

D2=（in［1］&0x04）》》2; D3=（in［1］&0x08）》》3;

D4=in［0］&0x01; D5=（in［0］&0x02）》》1;

D6=（in［0］&0x04）》》2; D7=（in［0］&0x08）》》3;

D8=in［3］&0x01; D9=（in［3］&0x02）》》1;

D10=（in［3］&0x04）》》2; D11=（in［3］&0x08）》》3;

D12=in［2］&0x01; D13=（in［2］&0x02）》》1;

D14=（in［2］&0x04）》》2; D15=（in［2］&0x08）》》3;

D16=in［5］&0x01; D17=（in［5］&0x02）》》1;

D18=（in［5］&0x04）》》2; D19=（in［5］&0x08）》》3;

D20=in［4］&0x01; D21=（in［4］&0x02）》》1;

D22=（in［4］&0x04）》》2; D23=（in［4］&0x08）》》3;

P7=0;

P6=0;

P5=D10^D11^D12^D13^D14^D15^D16^D17^D18^D19^D21^D22^D23;

P4=D4^D5^D6^D7^D8^D9^D16^D17^D18^D19^D20^D22^D23;

P3=D1^D2^D3^D7^D8^D9^D13^D14^D15^D19^D20^D21^D23;

P2=D0^D2^D3^D5^D6^D9^D11^D12^D15^D18^D20^D21^D22;

P1=D0^D1^D3^D4^D6^D8^D10^D12^D14^D17^D20^D21^D22^D23;

P0=D0^D1^D2^D4^D5^D7^D10^D11^D13^D16^D20^D21^D22^D23;

res = （（P7&0x01）*8+（P6&0x01）*4+（P5&0x01）*2+（P4&0x01））*16+（P3&0x01）*8+（P2&0x01）*4+（P1&0x01）*2+（P0&0x01）;

printf（“Result:0x%02X\r\n”，res）;

return 0;

}