

格雷码编码器功能实现
电子说
描述
编码器
编码器(encoder)是将信号(如比特流)或数据进行编制、转换为可用以通讯、传输和存储的信号形式的设备。编码器把角位移或直线位移转换成电信号,前者称为码盘,后者称为码尺。按照读出方式编码器可以分为接触式和非接触式两种;按照工作原理编码器可分为增量式和绝对式两类。增量式编码器是将位移转换成周期性的电信号,再把这个电信号转变成计数脉冲,用脉冲的个数表示位移的大小。绝对式编码器的每一个位置对应一个确定的数字码,因此它的示值只与测量的起始和终止位置有关,而与测量的中间过程无关。
格雷码
格雷码属于可靠性编码,是一种错误最小化的编码方式。因为,虽然自然二进制码可以直接由数/模转换器转换成模拟信号,但在某些情况,例如从十进制的3转换为4时二进制码的每一位都要变,能使数字电路产生很大的尖峰电流脉冲。而格雷码则没有这一缺点,它在相邻位间转换时,只有一位产生变化。它大大地减少了由一个状态到下一个状态时逻辑的混淆。由于这种编码相邻的两个码组之间只有一位不同,因而在用于方向的转角位移量-数字量的转换中,当方向的转角位移量发生微小变化(而可能引起数字量发生变化时,格雷码仅改变一位,这样与其它编码同时改变两位或多位的情况相比更为可靠,即可减少出错的可能性。
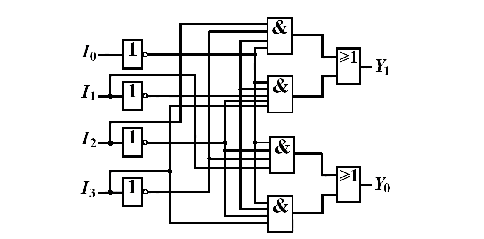
格雷码的实现
格雷码(Gray Code)是一个数列集合,每个数使用二进位来表示,假设使用n位元来表示每个数字,任两个数之间只有一个位元值不同。
例如以下为3位元的格雷码: 000 001 011 010 110 111 101 100 。
如果要产生n位元的格雷码,那么格雷码的个数为2^n.
假设原始的值从0开始,格雷码产生的规律是:第一步,改变最右边的位元值;第二步,改变右起第一个为1的位元的左边位元;第三步,第四步重复第一步和第二步,直到所有的格雷码产生完毕(换句话说,已经走了(2^n) - 1 步)。
用一个例子来说明:
假设产生3位元的格雷码,原始值位 000
第一步:改变最右边的位元值: 001
第二步:改变右起第一个为1的位元的左边位元: 011
第三步:改变最右边的位元值: 010
第四步:改变右起第一个为1的位元的左边位元: 110
第五步:改变最右边的位元值: 111
第六步:改变右起第一个为1的位元的左边位元: 101
第七步:改变最右边的位元值: 100
如果按照这个规则来生成格雷码,是没有问题的,但是这样做太复杂了。如果仔细观察格雷码的结构,我们会有以下发现:
1、除了最高位(左边第一位),格雷码的位元完全上下对称(看下面列表)。比如第一个格雷码与最后一个格雷码对称(除了第一位),第二个格雷码与倒数第二个对称,以此类推。
2、最小的重复单元是 0 , 1。
000
001
011
010
110
111
101
100
所以,在实现的时候,我们完全可以利用递归,在每一层前面加上0或者1,然后就可以列出所有的格雷码。
比如:
第一步:产生 0, 1 两个字符串。
第二步:在第一步的基础上,每一个字符串都加上0和1,但是每次只能加一个,所以得做两次。这样就变成了 00,01,11,10 (注意对称)。
第三步:在第二步的基础上,再给每个字符串都加上0和1,同样,每次只能加一个,这样就变成了 000,001,011,010,110,111,101,100。
好了,这样就把3位元格雷码生成好了。
如果要生成4位元格雷码,我们只需要在3位元格雷码上再加一层0,1就可以了: 0000,0001,0011,0010,0110,0111,0101,0100,1100,1101,1110,1010,0111,1001,1000.
也就是说,n位元格雷码是基于n-1位元格雷码产生的。
如果能够理解上面的部分,下面部分的代码实现就很容易理解了。
[java] view plain copypublic String[] GrayCode(int n) {
// produce 2^n grade codes
String[] graycode = new String[(int) Math.pow(2, n)];
if (n == 1) {
graycode[0] = “0”;
graycode[1] = “1”;
return graycode;
}
String[] last = GrayCode(n - 1);
for (int i = 0; i 《 last.length; i++) {
graycode[i] = “0” + last[i];
graycode[graycode.length - 1 - i] = “1” + last[i];
}
return graycode;
}
格雷码还有一种实现方式是根据这个公式来的 G(n) = B(n) XOR B(n+1), 这也是格雷码和二进制码的转换公式。代码如下:
[java] view plain copypublic void getGrayCode(int bitNum){
for(int i = 0; i 《 (int)Math.pow(2, bitNum); i++){
int grayCode = (i 》》 1) ^ i;
System.out.println(num2Binary(grayCode, bitNum));
}
}
public String num2Binary(int num, int bitNum){
String ret = “”;
for(int i = bitNum-1; i 》= 0; i--){
ret += (num 》》 i) & 1;
}
return ret;
}
这是一道google 的面试题,以上代码均是网友peking2 和 SEwind520写成。原题还要求把二进制码转成十进制数。
全部0条评论

快来发表一下你的评论吧 !

