

弛豫频率与截止频率计算
描述
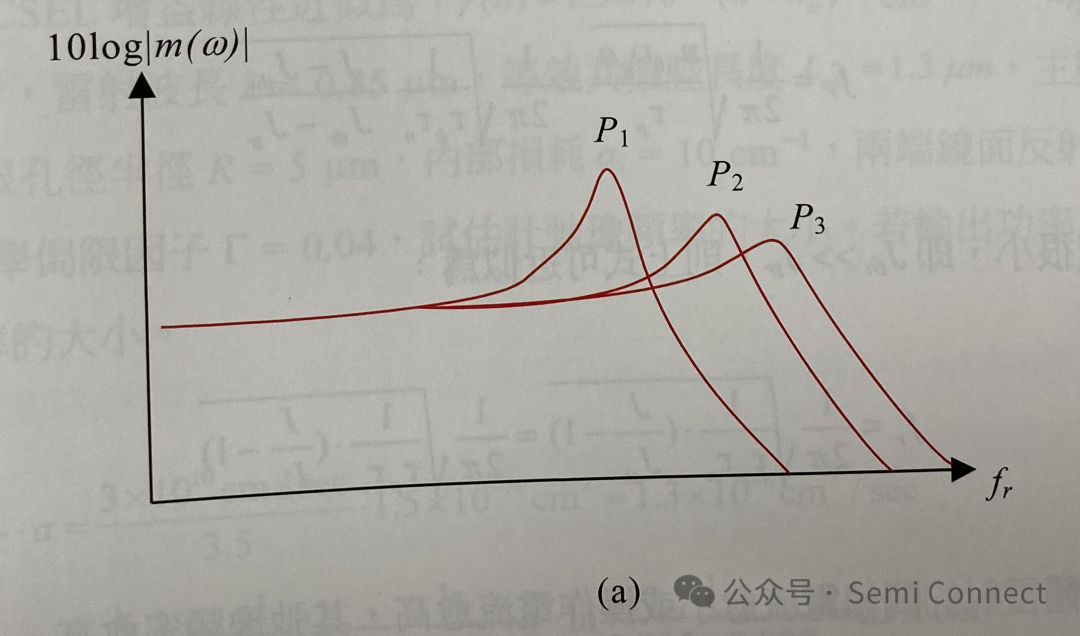
(4-25) 式为我们可以量测得到的半导体雷射调制响应。将之取对数乘上10之后,其单位即为 dB,如图 42所示。当小信号频率远小于弛豫频率时,(4-25)式可以近似成1,也就是小信号的输出振幅和稳态时所获得的振幅相同,相位也一致。当小信号频率接近弛豫频率时,我们可以发现调制响应的曲线中会出现一个峰值,此峰值的频率可以借由计算(4-25)式的分母中找到最小值获得:

而在W=Wp时,调制响应的峰值为:
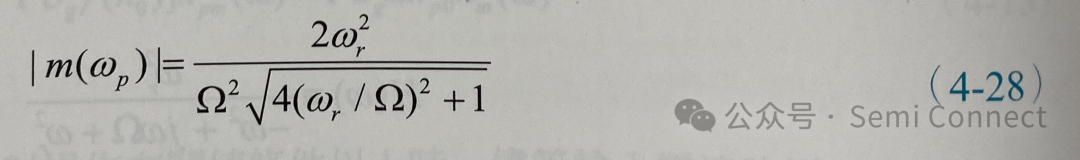
由上二式可知,峰值的频率与调制响应峰值的大小与Wr/Ω 相关,在一般常用的半导体雷射中,弛豫频率通常都远大于阻尼常数,因此Wr/Ω远大于1,使得峰值的频率即可代表为弛豫频率,而调制响应峰值的大小则趋近于Wr/Ω。因此,弛豫频率可以代表此雷射系统的共振频率,当雷射操作于此频率时,小信号的输出会有最大的振幅,不过在相位方面也会伴随着剧烈的变化。
相反的,若雷射系统中的阻尼常数愈来愈大,将会使得调制响应的峰值下降,如图4-2中Wr/Ω=1的情况,共振现象变得不明显,而峰值频率也会小于弛豫频率。这是因为阻尼常数会使得系统的振荡振幅迅速衰减,导致调制响应的表现趋于平缓,关于阻尼常数的意义,会在稍后章节讨论。
在调制响应中,若输入小信号的频率远大于弛豫频率,(4-25)式将会趋近于零,这表示在此高频率操作的情况下,雷射的输出小信号振幅跟不上输入信号的变化,使得雷射系统趋于稳态。为了定义雷射的系统何时会趋于稳态,我们定义当输出小信号振幅降为低频振幅的一半时的频率范围为此雷射的操作频宽,而此频率被称为3dB 频率(W3dB)或
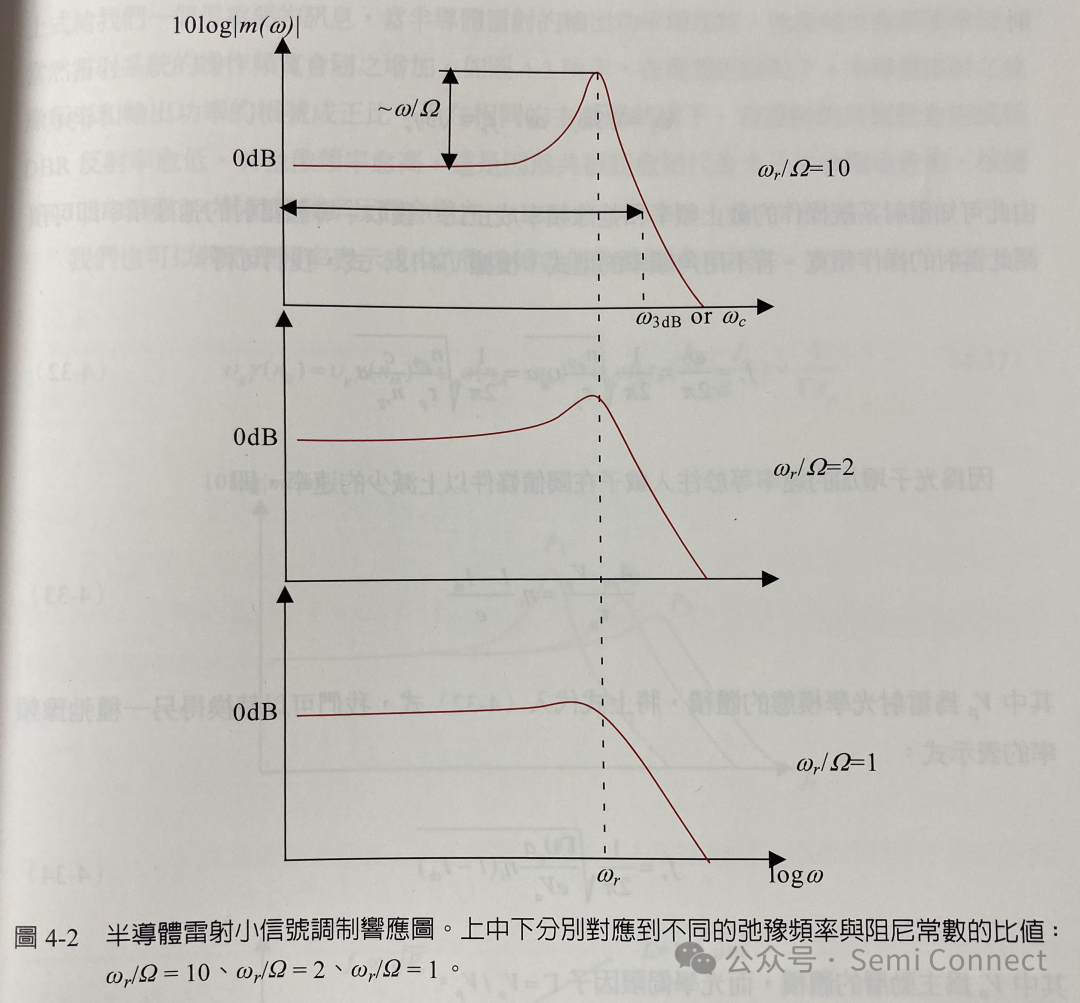
是截止频率(cut-off frequency,Wc)。因此根据定义:
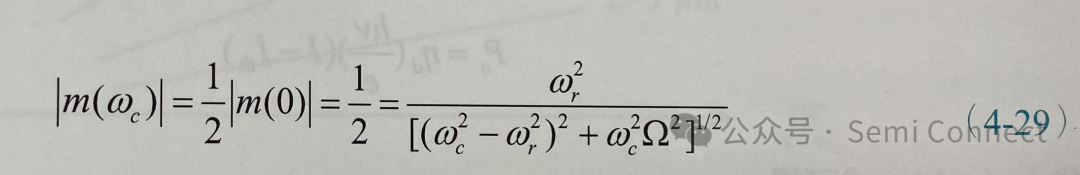
假设Wc2Ω2
则
由此可知雷射系统操作的截止频率和弛豫频率成正比,获取半导体雷射的弛豫频率即可预测此雷射的操作频寛。若不用角频率的型式,根据(4-18)式,我们可得:
因为光子增加的速率等于注入载子在阈值条件以上减少的速率,即:
其中Vp为雷射光学模态的体积,将上式代入(4-32)式,我们可以替换得另一种弛豫频率的表示式:
其中 Va为主动层的体积,
我们也可以将上式中电流的部分替换成雷射的输出功率,由于:
代入(4-34)式可得:
上式给我们一个很重要的讯息,当半导体雷射的输出功率增加时,弛豫频率会跟着增加,当然雷射系统的操作频宽会随之增加。如图4-3所示,在理想的情况下,半导体雷射之弛豫频率和输出功率的根号成正比;而在相同的主动层结构下,若雷射的共振腔愈短或是DBR 反射率愈低,其弛豫频率愈高,这是因为共振腔愈短代表光子生命期也愈短,根据(4-32)式可知,其弛豫频率反而会变大。
我们也可以将弛豫频率表示式中的微分增益系数替换掉,由于:
因此,
此外,由(4-33)式,
将(4-38)式与(4-39)式代入(4-32)式中,可得:
若透明电流密度很小,即Jth>>Jtr,则上式可近似为:
此式说明了半导体雷射的阈值电流愈小或操作电流愈高,其弛豫频率愈高。
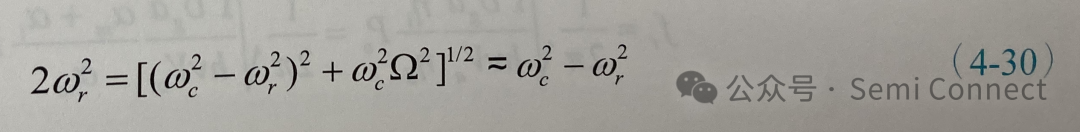
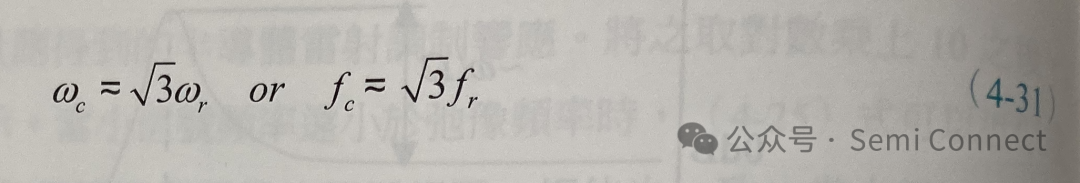
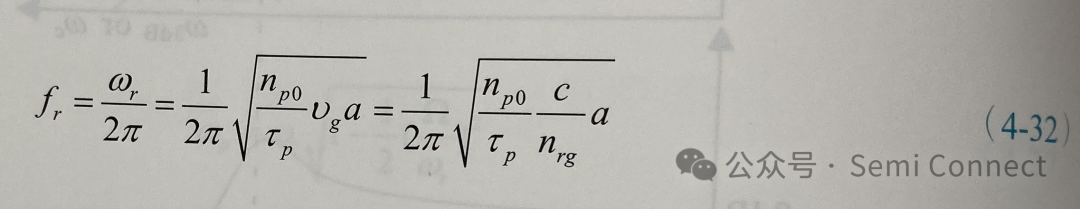


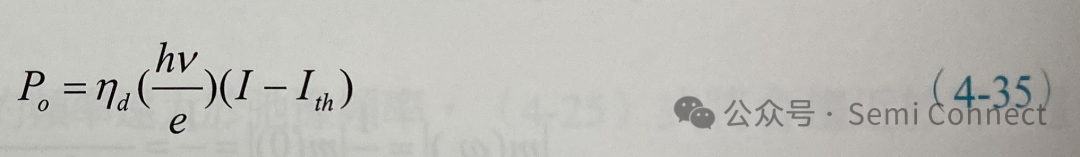
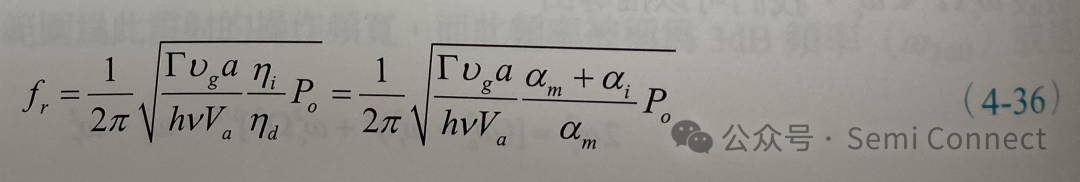
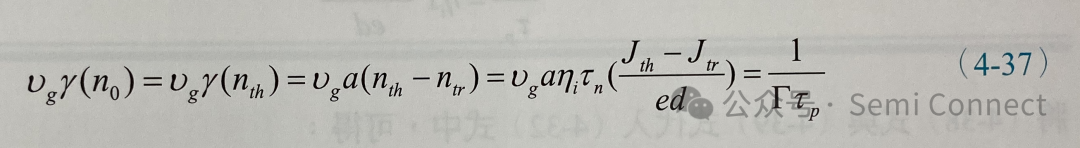



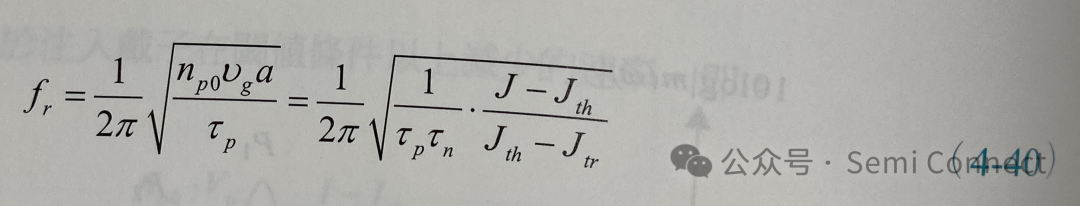
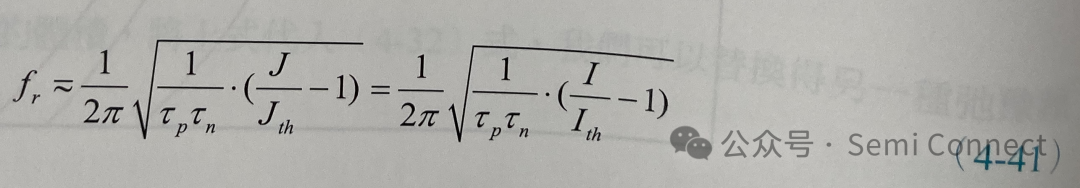
-
电源滤波器的截止频率是什么2024-12-03 1732
-
放大器的截止频率怎么算?2024-01-17 3551
-
二阶巴特沃斯滤波器电路截止频率计算公式2023-12-15 15142
-
lc滤波器的截止频率计算公式2023-12-14 17068
-
滤波器的截止频率分析2023-09-27 9276
-
低通滤波器的截止频率和采样频率2023-09-12 24797
-
滤波器的截止频率如何定义2023-02-16 10874
-
这种低通滤波器截止频率计算2022-11-03 15454
-
截止频率计算2022-08-02 14128
-
开环截止频率和闭环截止频率的相关资料推荐2021-11-16 1803
-
截止频率仿真与计算值不符2021-09-26 5112
-
请问什么是截止频率,如何计算截止频率?2018-08-04 36291
-
什么是特征频率/截止频率2010-03-05 28254
全部0条评论

快来发表一下你的评论吧 !

