半导体雷射之发光线宽

从前面的例子中，可以知道线宽增强因子会让半导体雷射在动态操作时谱线变宽，接下来我们要讨论的是半导体雷射在稳态操作下的发光线宽。

同样的，假设在一单模操作的雷射中，雷射光在共振腔中沿着z方向行进，我们可以将雷射光的电场表示为：

其中E（t）代表了电场对时间变化较缓慢的包络，可表示为

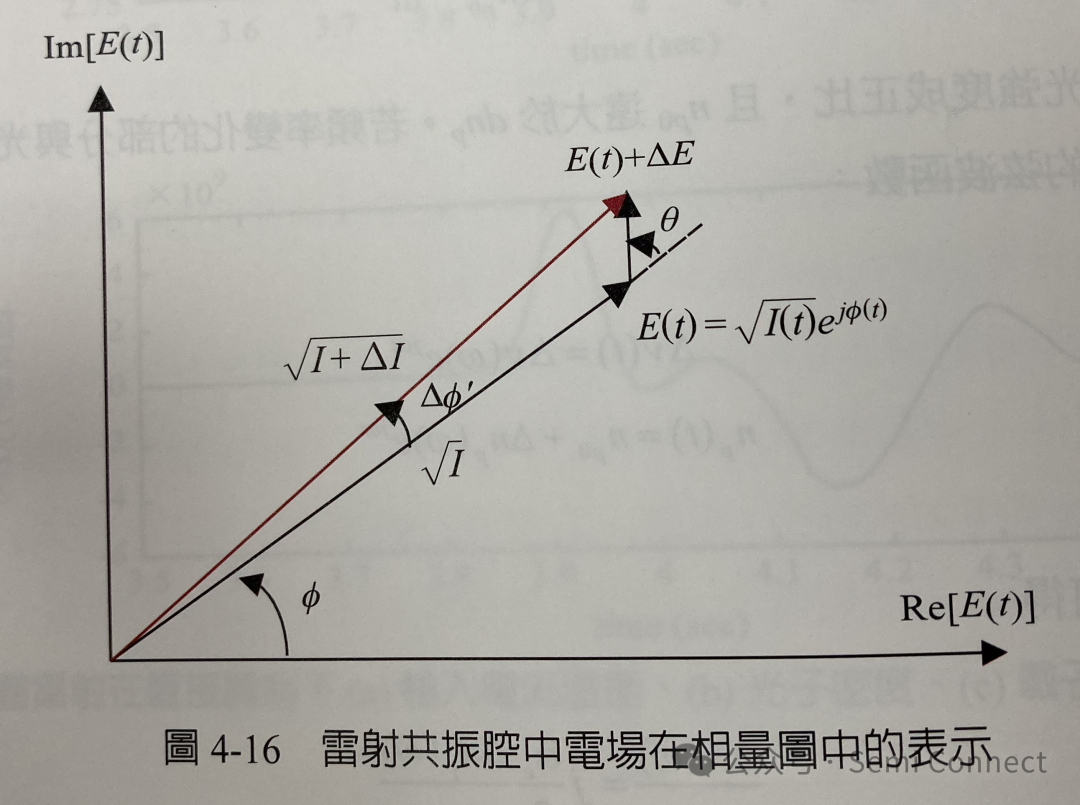
w为雷射光的振荡角频率，I（t）是指光场强度和光子数目成正比，我们可以将其正规化并使其代表雷射共振腔内的平均光子数目，而Φ（t）是指此电场包络的相位，我们可以用相量图（phasor plot ）来表示此电场如图4-16所示，E（t）以w的角频率在旋转。假设有一随机的自发辐射△E改变了原本E的状态到E+△E，其中

为方便起见，△E的大小被正规化为1。因此电场的相位被改变了△Φ，而影响△Φ的因素有两个，表示成

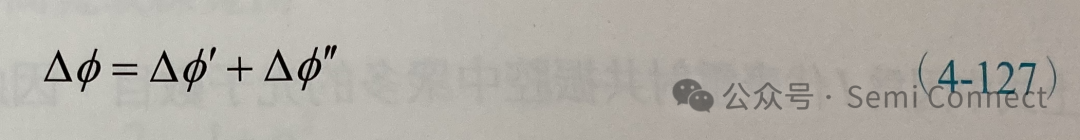
第一个影响△Φ的因素是由于自发辐射 △E 的加入使得电场相位随之改变的部分△Φ，这项自发辐射的因素会对所有种类的雷射产生影响，由图4-16可知

而第二个影响△Φ的因素是光场强度的改变（△I）使得相位发生改变△Φ”，这项因素特别会对半导体雷射产生影响，因为增益和折射率都会受到载子浓度与光场强度变化的影响，因此我们可以使用上式得到：

在这里我们忽略（4-113）式中的负号只取其变化量的大小，相位改变量 △Φ可表示为：

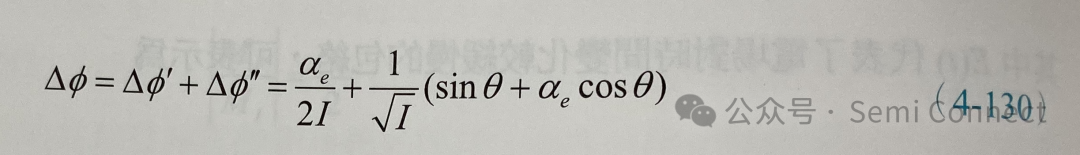
（4-130）式只是一个自发辐射所造成的相位改变量，若将上式在时间t之内对所有的自发辐射积分并取平均值，我们可以得到平均的总相位变化量：

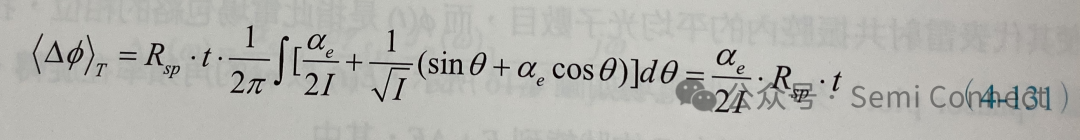
其中 Rsp为贡献到雷射模态的自发辐射速率（因此我们略掉自发放射因子β）。同理：

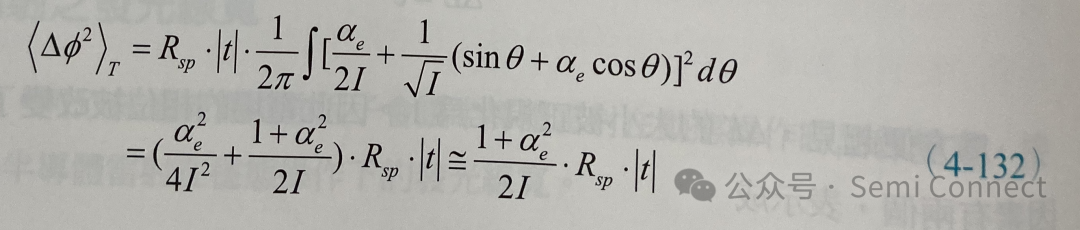
上式中因为I代表雷射共振腔中众多的光子数目，因此a2e/4I2趋近于零。

接下来要计算雷射发光的强度频谱以获取半导体雷射之发光线宽，我们可以将电场相关函数作傅立叶转换来计算强度频谱：

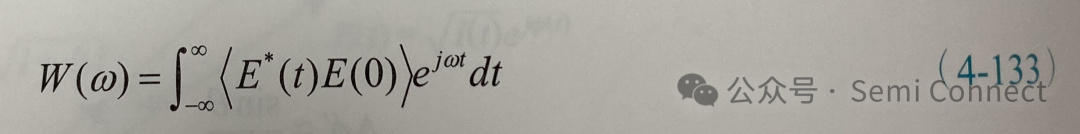
若换成光强度，则上式变为：

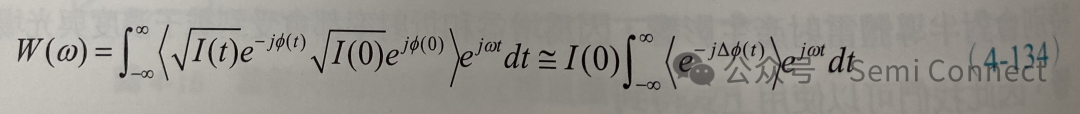
因为自发辐射的事件是随机发生的，我们可以假设相位变化的机率 P（△Φ）是Gaussian 形式的机率分布函数，因此：

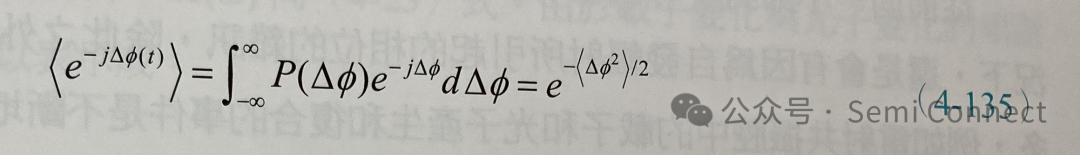
若定义同调（coherent）时间tc为

将上式和（4-132）式比较可知：

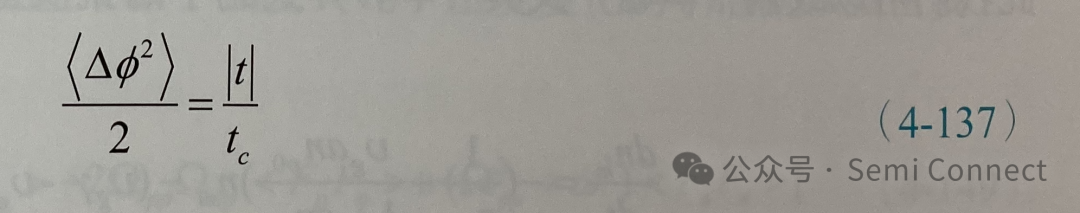
因此，（4-134）式可表示为

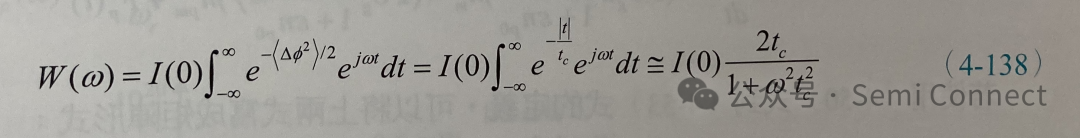
上式为 Lorentzian 函数的型式，其半高宽或线宽为：

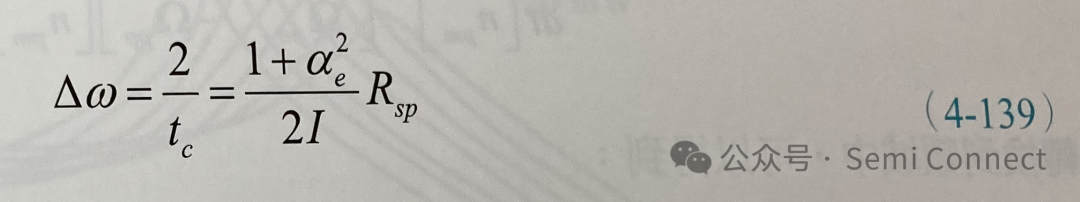
或是

其中Rsp/4兀I为一般雷射线宽的量子极限，被称为 Schawlow-Townes 线宽，而在半导体雷射中线宽增强因子使得原本雷射线宽以平方的倍数来增加线宽，这也是ae这个参数的名称缘由。