卡尔曼滤波基础知识

附录：补充材料

附1、卡尔曼滤波主要框架？

卡尔曼滤波的本质属于系统的最优估计，通过卡尔曼增益来修正状态预测值，减小噪声信号对测试精度的影响，其核心内容是基于上一时刻状态的估计值以及当前状态的观测值，给出当前状态的最优估计，该算法涉及的核心方程有：

其中，xt为系统状态矩阵；zt为系统观测矩阵（实验结果）；A为状态转移矩阵；B为控制输入矩阵；H为状态观测矩阵。

附2、卡尔曼滤波应用实例？

本部分通过简单的算例，介绍了卡尔曼滤波的应用场景，后续针对课题组实际需求，编写了能够应用于大应变传感器的滤波程序，具体如下所示：

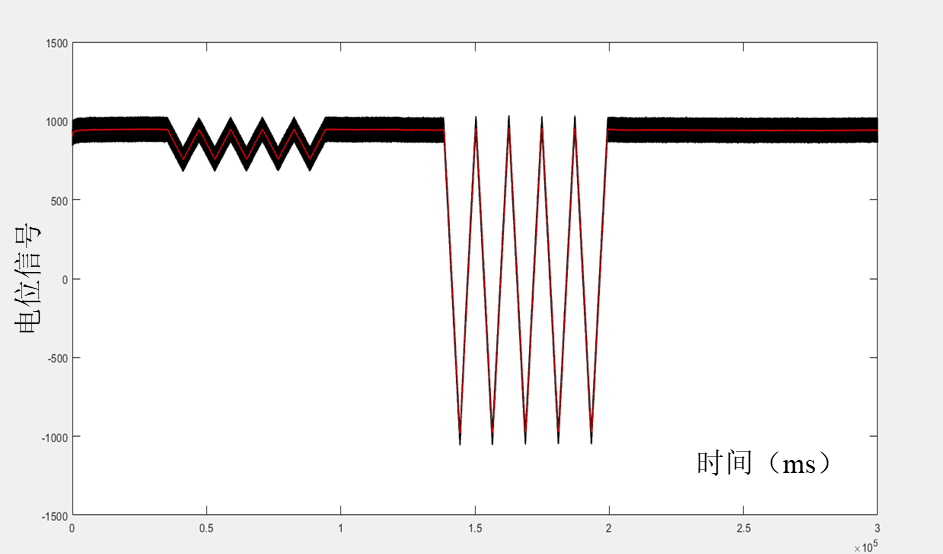
上图中黑线表述为信号采集系统得到的原始信号，红线表述为卡尔曼滤波后展现的信号特征；从图中可以看出，卡尔曼滤波能够有效地减小测量误差；其中，状态转换矩阵A=1,具体物理意义为：传感器输出信号只与应变量相关，不施加外界激励时，输出信号不发生改变；状态观测矩阵H=1,具体物理意义为：传感器输出的信号能够直接测量；

具体使用的源程序代码如下：

clear all;clc
%先对不同变量进行定义
% Q为过程激励噪声协方差
% R为观测噪声协方差
% X_bar为先验证估计
% Xbar为后验估计，最优估计值
% P_为先验估计误差协方差
% P为后验估计误差协方差
% Z为测量结果，测量数据（实验结果）
% K为卡尔曼增益


% 核心代码


% 读取传感器输出信号
node='信号采集结果.txt';
[x,Z]...
    =textread(node,'%f%f','emptyvalue',0,'headerlines',10);


% 定义超参数：实验数据长度，过程激励噪声协方差，观测噪声协方差(测量设备性能参数)
changdu=length(Z);
Q=0.04;
R=100.25;


% 定义尺寸参数
cicun=[changdu,1];


% 实验数据
% Z=24+sqrt(R)*randn(cicun);


% 定义初始迭代参数
X_bar=zeros(cicun);
Xbar=zeros(cicun);
K=zeros(cicun);
P_=zeros(cicun);
P=zeros(cicun);


P(1)=1;
Xbar(1)=900.3;


% 卡尔曼滤波参数更新
for n=2:changdu
%   更新先验估计
    X_bar(n)=Xbar(n-1);
%   更新先验估计误差协方差
    P_(n)=P(n-1)+Q;
% 状态更新
    K(n)=P_(n)/(P_(n)+R);
    Xbar(n)=X_bar(n)+K(n)*(Z(n)-X_bar(n));
    P(n)=(1-K(n))*P_(n);
end


% 绘图
plot(Z,'K+')
hold on
plot(Xbar,'r-')
hold on