机器学习如何应对失衡类别

前言

实际应用中的分类问题往往不像教科书上人造的例子那样齐整，类别往往存在某种程度上的失衡。Towards Data Science博主Devin Soni简要介绍了应对失衡分类的常用方法。

介绍

大多数真实世界的分类问题都呈现出某种程度的类别失衡，即每个类别在数据集中的比例不同。恰当地调整指标和方法以适应目标非常重要。否则，你可能最终会为一个对你的用例无意义的度量指标进行优化。

例如，假设你有两个类——A和B。A类占数据集的90％，B类占10％，但你最感兴趣的是识别B类的实例。你可以每次都预测分类为A，这样轻易就能达到90%的精确度，但对你的预期用例而言，这是一个无用的分类器。相反，经过恰当地校准的方法可能精确度较低，但会有较高的真阳率（或召回），这才是你应该优化的指标。在进行检测时，这是常常发生的场景，例如检测在线恶意内容或医疗数据中的疾病标记。

现在我将讨论几种可以用来缓解类别失衡的技术。一些技术适用于大多数分类问题，而其他技术可能更适合具备特定的失衡水平的问题。本文将从二元分类的角度来讨论这些问题，但大多数情况下，这些技术同样适用于多类分类问题。本文同时假设目标是识别少数类别，否则，这些技术并不是真的很有必要。

指标

一般来说，这个问题涉及召回率（recall，真阳性实例被分类为阳性实例的百分比）和准确率（precision，被分类为真阳性的实例中确实是阳性的百分比）之间的折衷。当我们想要检测少数类别实例时，我们通常更关心召回率而不是准确率，因为在检测的情境中，错过正面实例的成本通常高于错误地标记负面实例为正面实例。例如，如果我们试图检测恶意内容，那么手动审核纠正被误认为恶意内容的正常内容是微不足道的，但要识别甚至从未被标记为恶意内容的内容就要困难很多了。因此，比较适用于失衡分类问题的方法时，请考虑使用精确度之外的指标，例如召回率，准确率和AUROC。在选择参数和模型时，切换优化指标可能就足以提供侦测少数类别所需的表现。

成本敏感学习

在通常的学习中，我们平等对待所有错误分类，这在失衡分类问题中会导致问题，因为相比识别出主要类别，识别出少数类别并不会有额外的奖励。成本敏感学习改变了这一点，使用函数C(p, t)（通常表示为矩阵）指定将t类实例错误分类为p类实例的成本。这让我们可以给错误分类少数类别更多的惩罚，以便增加真阳率。一个常用的方案是让成本等于类别在数据集中所占比例的倒数。这样，当类别尺寸缩小时，惩罚会增加。

采样

解决失衡数据集的一个简单方法就是平滑它们，过采样少数类别，或者欠采样主要类别。这让我们创建一个平衡的数据集，理论上能使分类器不偏向其中一个类。然而，这些简单的采样方法实际上存在缺陷。过采样少数类别会导致模型过拟合，因为它会引入从已经很小的实例池中抽取的重复实例。同样，欠采样主要类别可能最终导致遗漏体现了两个类别之间的重要差别的重要实例。

还存在比简单的过采样或欠采样更强大的采样方法。最着名的例子是SMOTE，SMOTE通过构建相邻实例的凸组合来创建少数类别的新实例。如下图所示，它有效地绘制了特征空间中少数点之间的线条，并沿着这些线条采样。这使我们能够平衡我们的数据集，而不会过多地过拟合，因为我们创建了新的合成示例，而没有使用重复样本。不过这并不能防止所有过拟合，因为这些合成数据点仍然是基于现有数据点创建的。

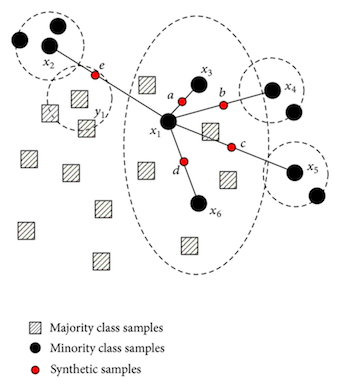
可视化SMOTE。阴影方块：主要类别样本；黑点：少数类别样本；红点：生成样本

异常侦测

在更极端的情况下，将分类问题考虑成异常检测（anomaly detection）问题可能会更好。在异常检测问题中，我们假设有一个或一组“正常”的数据点分布，而任何与该分布足够偏离的东西都是异常值。将分类问题置于异常检测的框架下以后，我们将主要类别视为点的“正常”分布，将少数类别视为异常。有许多用于异常检测的算法，例如聚类（clustering）方法，单类SVM（One-class SVM）和孤立森林（Isolation Forests）。

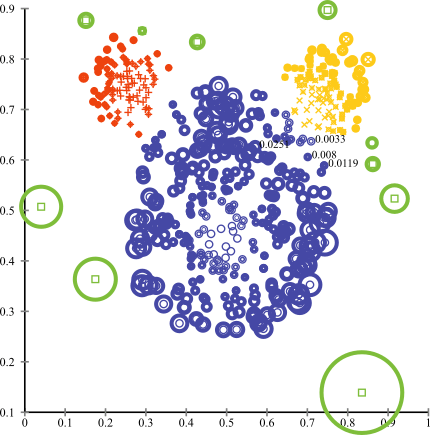
可视化用于异常检测的聚类方法

结论

希望这些方法的某些组合可以让你创建一个更好的分类器。像我之前说的那样，这些技术中的某些技术更适合不同程度的失衡。例如，简单的采样技术可以让你克服轻微失衡，而极端失衡可能需要异常检测方法。基本上，对于这个问题，没有包治百病的灵丹妙药，你需要尝试每种方法，看看它们应用到你的特定用例和指标的效果如何。