非线性电路的混沌现象

1、引言

混沌理论（ChaosTheory）是架起确定论和概率论两大理论体系之间的桥梁，与相对论、量子力学一起被称为20世纪物理学的三大科学革命。混沌研究最先起源于1963年洛伦兹（E.Lorenz）研究天气预报时用到的三个动力学方程，后来又从数学和实验上得到证实。混沌来自非线性，是非线性系统中存在的一种普遍现象。无论是复杂系统，如气象系统、太阳系，还是简单系统，如钟摆、滴水龙头等，皆因存在着内在随机性而出现类似无轨、但实际是非周期有序运动，即混沌现象。近年来，混沌现象及其应用已成为通讯工程、电子工程、生物工程、经济学等领域中的一个研究热点。由于电学量（如电压、电流）易于观察和显示，因此非线性电路逐渐成为混沌及混沌同步应用的重要途径，其中最典型的电路是美国加州大学伯克利分校的蔡少棠教授1985年提出的著名的蔡氏电路（Chua’sCircuit）。蔡氏电路是能产生混沌行为的最简单的自治电路，是至今所知唯一的混沌实际物理系统，已被希尔尼柯夫定理严格证明存在混沌现象。就实验而言，可用示波器观察到电路混沌产生的全过程，并能得到双涡卷混沌吸引子，有兴趣的读者不妨亲自搭试电路，实际观测一番。

2、蔡氏电路

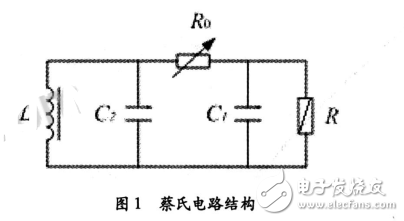
图1就是讨论非线性电路系统的一种简单而又经典的电路———蔡氏电路，它是由两个线性电容C1和C2、一个线性电感L、一个可变线性电阻R0和一个非线性电阻R构成。电感L和电容C2并联构成振荡电路，线性电阻R0的作用是分相。非线性电阻R的伏安特性iR=g（uR），是一个分段线性的负电阻，如图2所示，整体呈现对称但非线性。负阻是出现混沌的原因，其特性至少可用三种方法来实现：两个晶体管和两个二极管;一个运算放大器和两个二极管;一个双运算放大器和六个线性电阻组合。

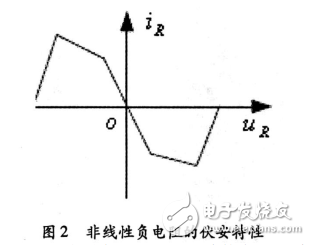
图1电路中有3个状态变量uC1，uC2和uL，电路的非线性动力学状态方程为：

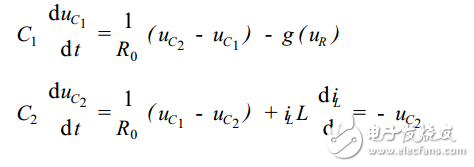
式中：uC1，uC2和iL分别表示C1、C2两端的电压，L中的电流。g（uR）是负阻曲线。蔡氏电路是能产生混沌行为的最小、最简单三阶（3个状态变量）自治（方程右端不显含时间）电路。

3、电路混沌的实验研究

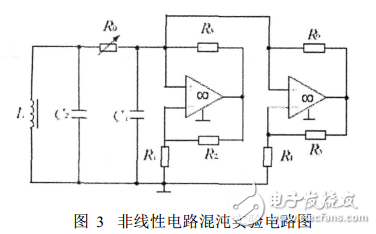
混沌实验电路如图3所示。这里将蔡氏电路中的非线性电阻R的特性通过一个双运算放大器和6个线性电阻组合来实现，具体参数选取如下：R1=5.1kΩ，R2=3.3kΩ，R3=1kΩ，R4=R5=100Ω，R6=5.6kΩ。每次取两个状态变量在示波器上观察李萨如图形。

3.1、改变电阻R0，其它参数保持不变。

在合适选取C1、C2和L以后，如取C1=4700pF，C2=0.1μF，L=10mH，调节R0。当R0由3kΩ逐渐减小时，在示波器上看到，例如由uC1-uC2呈现的变化规图3非线性电路混沌实验电路图律。由1个点（稳态平衡点）→1个圈（Hopf分岔，出现单周期极限环）→2个圈（倍周期分岔，出现2周期极限环）→22圈（4周期极限环）→……→2∞个圈（单涡卷混沌吸引子）。实验中一般能观察到周期8，由于变化速度太快很难看到大于8的周期。周期为无穷大也就是没有周期，这就是混沌。在上述参数值下，R0=1.5kΩ左右时电路可进入混沌状态。继续减小R0，还会出现双涡卷混沌吸引子，只见环形曲线在两个外涡卷的吸引子之间不断填充与跳跃，这就是混沌研究文献中所描述的“蝴蝶”图像，也是一种奇异吸引子，它的特点是整体上的稳定性和局部上的不稳定性同时存在。图4是一个单涡卷混沌吸引子，图5、图6都是双涡卷混沌吸引子。

利用这个电路，还可以观察到周期性窗口，仔细调节R0，有时原先的混沌吸引子不是倍周期变化，却突然出现了一个三周期图像，再微调R0，又出现混沌吸引子，这一现象称为出现了周期性窗口。
#p#

混沌现象的本质

#e#

3.2、调节电容C1（或C2）。

固定C2（或C1）、L和R0在某一适当的数值，改变C1（或C2）所得分岔和混沌规律与1中相类似。

3.3、改变负阻曲线。

在1、2中都是保持负阻曲线对称不变的情况下调节电路参数观察到的结果。在合适选取C1、C2、L和R0以后，调节其中一个运算放大器的电源电压改变负阻曲线，也能得到漂亮的混沌规律。

4、混沌现象的本质

混沌是一种确定系统中出现的貌似不规则的有序运动。这种有序是乱中有序，是有序与无序的结合，是非线性序———混沌序。变是混沌的本性。分岔是进入混沌的途径。随着时间的推移，系统运动状态在不断变化。当控制参量λ（λ=0对应于平衡态）由小到大变化时，系统由稳定有序逐渐失稳，开始分岔，随着分岔按几何级数的不断增长，系统由有序到无序。当控制参量达到一个临界值时系统进入混沌区，当再增大时又会遇到一个个的周期窗口，一个个混沌区……当控制参量不断减少时系统又会由混沌逐渐向有序演化。现已知道在倍周期分岔进入混沌的过程中存在一个普适常数———费根鲍姆常数（Feigenbaumcontant），即

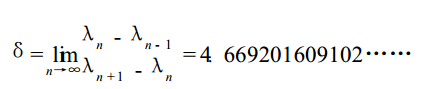
上式中λn是第n次分岔出现的参数值，δ是相继分岔的间距之比的极限，是一个类似π、e和普朗克常数的无理数。这是美国物理学家费根鲍姆利用计算机在1978年计算发现的。现已有数学家用泛函方法得到证明。费根鲍姆常数的存在反映了混沌演化过程中的有序性。

5、结语

电路混沌的研究不仅有助于揭示非线性电路的本质，发现新规律，也有助于将这些结果直接应用到其他学科中去，因为描述各种系统中的运动方程有时是类似的。混沌电路的实验研究仍是一个很有前途的研究领域。本文通过蔡氏电路介绍了最基本的混沌概念，说明了如何实现5段分段线性的非线性负阻以及观察混沌的三种方法，表明蔡氏电路虽然结构非常简单，但其非线性动力学行为极其丰富，Feigenbaum倍周期分岔过程是蔡氏电路中典型的通向混沌道路。这一内在规律在完全不同的非线性电路系统中都会出现，具有普适性。感兴趣的读者不妨亲自试一试，蔡氏电路的应用研究目前也取得了丰硕的成果。特别是蔡氏电路易于控制和同步，既可以控制它由混沌状态转变为周期性或定常轨道，也可以使两个相同的蔡氏电路同步工作于周期振荡或混沌状态，使混沌电路有可能在广泛的领域中得到应用，如混沌保密通信技术、数字水印技术和混沌扩频通信技术等等。