线性电阻电路的分析方法_线性电阻的串并联

1、支路电流法和结点电压法

支路电流法是以支路电流为电路变量，对于有n忍个结点、b条支路的电路，可以对任意（n—1）个结点列出（n—1）个独立的KCL方程，对电路中的独立回路列出（b一（n—1）］个KVL方程，然后求出各支路电流的1种基本的方法。它的要点是：首先对各支路电流标出参考方向；找（n一1）个结点应用基尔霍夫电流定律列电流方程；找（b—n+1）个独立回路应用基尔霍夫电压定律列电压方程，联立方程组求解即可。

在各种电路分析方法中，结点电位法是1种通用的分析方法，结点电压法是结点电位法的特例，尤其适用于结点数少而连接支路多的电路。目前使用的计算机辅助分析软件一般都以结点电位分析法为基础。利用这个方法把求解某电流、电压响应的问题转化为求1个或几个结点电压的问题。此方法的要点是确定结点电压（电位），首先在电路中选定1个结点为参考电位点，然后根据KCL对各独立结点列写结点电位（压）方程。

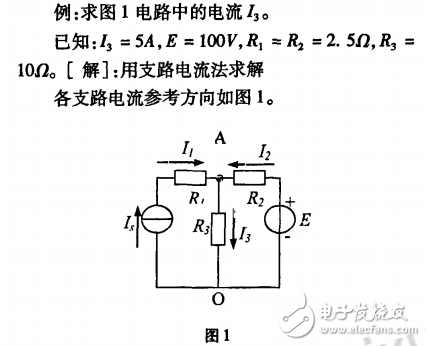
本例题中的电路有2个结点，两结点间有3条支路，用结点法求解更简单。以上计算过程说明：支路电流法一般用于结点间联接支路数不是太多的电路，否则需列写的方程组较多，给计算带来不便；当电路中的独立节点数（n一1）小于支路数b时，应选择结点电压法求解。

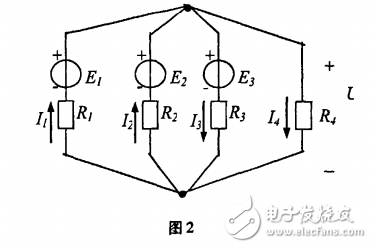
如图2所示，电路中有4条支路，若用支路电流法求解需解四元一次方程组，比较复杂；而电路中只有2个结点，即仅有1个独立结点，所以用结点电压法求解较方便。

#p#

叠加原理和等效电源定理

#e#

2、叠加原理和等效电源定理

叠加原理是分析线性电路时普遍适用的基本原理。使用叠加原理时，要把原电路分成几个分电路，先求出各分电路的电压或电流，然后求代数和得出原电路的总电压或总电流。方法要点：首先标定原电路各支路电流、电压的参考方向；将电路分解为各理想电源单独作用的分电路，标出各分电路中电流（电压）的参考方向；求解分电路中各支路电流（电压）；最后叠加求解出原电路的电流（电压）响应一求各分电路对应支路电流（电压）代数和，凡分电路电流（电压）参考方向与原电路电流（电压）参考方向一致者取正号，反之取负号，但保留分电流本身的符号。

图1电路用叠加原理求解，由于原电路中有两个独立电源，所以可把原电路用2个简单电路叠加表示。

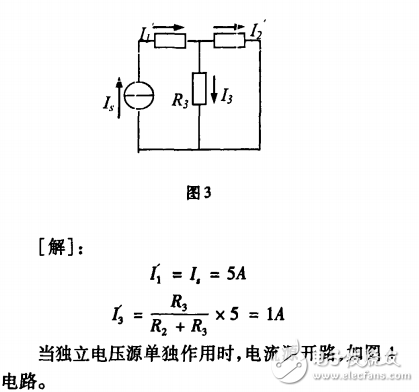
当电流源单独作用时，电压源短接。如图3所示电路。

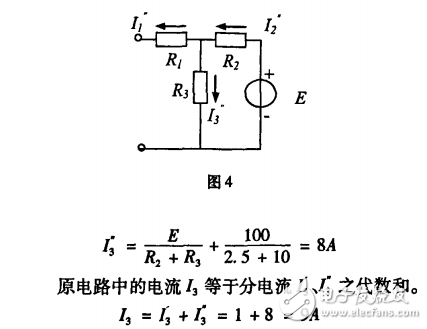
当然对图2电路需要对3个分电路分别计算，然后再叠加。即当独立电源较多时，这一方法就不可取了。一般叠加原理用于计算电路结构较复杂但独立电源不多的电路。

当1个复杂电路只需求解其中1条支路的电流或电压时，那么用等效电源定理就比较方便。一般情况下，任何线性有源二端网络可以用1个电动势为E的理想电压源和内阻Ro串联的电源来等效代替，该定理就是戴维宁定理；或者等效成电流为I。的理想电流源和等效电阻Ro的并联组合代替，即诺顿定理。

对图2电路若只求R4支路电流。用戴维宁定理求解就比较方便。

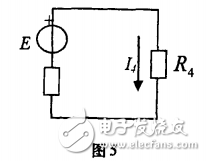
［解］：其戴维宁等效电路如图5，其中的等效电势E等于把毗支路开路时的端口开路电压，如图6所示电路；

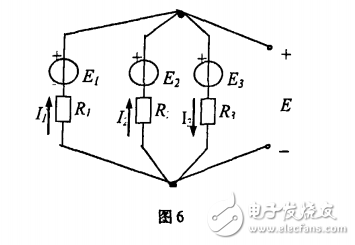
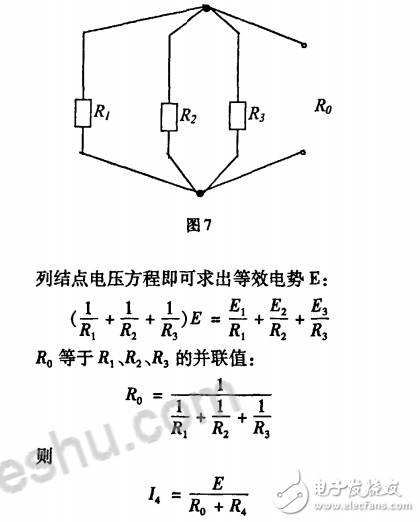
通过以上实例对比，给我们在分析电阻电路时的启示有：电阻电路的分析和计算的最佳方法选择应根据电路的结构和要求来确定。在支路数不多且要求解各支路电流的电路可以选择用支路电流法；在电路结点数少，但结点间联接的支路较多的电路可以选择结点电压法；在电路结构复杂但电路中独立电源不多的电路分析求解时可以选择叠加原理；等效电源定理是1种简单有效的方法，往往适用于只求一部分电路的电流或电压。

3、线性电阻电路分析

1.线性电阻的串联

两个二端电阻首尾相联，各电阻流过同一电流的连接方式，称为电阻的串联。图（a）表示n个线性电阻串联形成的单口网络。

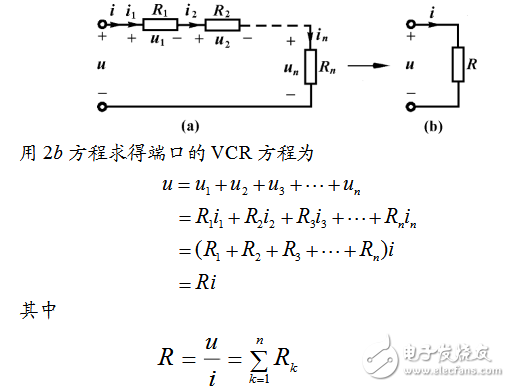
上式表明n个线性电阻串联的单口网络，就端口特性而言，等效于一个线性二端电阻，其电阻值由上式确定。

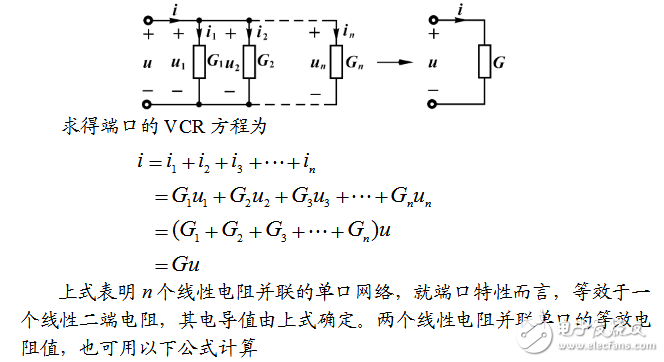
2.线性电阻的并联

两个二端电阻首尾分别相联，各电阻处于同一电压下的连接方式，称为电阻的并联。图（a）表示n个线性电阻的并联。

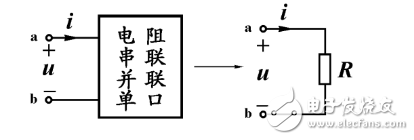
3.线性电阻的串并联

由若干个线性电阻的串联和并联所形成的单口网络，就端口特性而言，等效于一个线性二端电阻，其等效电阻值可以根据具体电路，多次利用电阻串联和并联单口的等效电阻公式（2－1）和（2－2）计算出来。