一文看懂复阻抗和阻抗的区别

　　复阻抗的概念

　　在关联参考方向下，正弦交流电路中任一线性无源单口的端口电压相量与电流相量的比称为该单口的复阻抗，用Z表示，即：Z==|Z|《Ψz。显然复阻抗也是一个复数，但它不在是表示正弦量的复数，因而不是相量。在电路图中有时用电阻的图形符号表示复阻抗。

　　复阻抗是反映一段无源电路或无源二端网络电性质的物理量。在交流电路的复数解法中，把电压电流等简谐量都用其对应复数表示，分别称为复电压、复电流。一段无源电路上复电压、复电流的比称为复阻抗。复阻抗的辐角等于电压电流的位相差，称为阻抗角。复阻抗的代数式表为Z=r+jX。式中复阻抗的实部r称为有功电阻，复阻抗的虚部X称为电抗。纯电阻的复阻抗Z=R，纯电感元件的复阻抗Z=jωL，其量值XL=ωL，称为感抗。纯电容元件的复阻抗Z=1/jωC=-j1/ωC，其量值Xc=1/ωC称为容抗。

　　复阻抗的概念可以推广到任一无源二端网络，无源二端网络上复电压与复电流的比称为无源二端网络的复阻抗，表为Z=U/I。式中U为无源二端网络两个引出线端之间的电压复有效值；I是通过二端网络的电流复有效值。复阻抗既反映了这段电路阻抗的大小（用复阻抗的模表示），又反映在这段电路上电压与电流间的位相差（用复阻抗的辐角表示）。所以复阻抗比阻抗有更丰富的内容。

　　由复阻抗的定义式Um=ImZ或U=IZ，它与直流欧姆定律有相同的形式，称为复数形式的欧姆定律。引入复电压、复电流、复阻抗后使得交流电路规律的表达式变得非常简洁。

　　复阻抗谱分析

　　复阻抗谱分析是对固体电解质进行电化学研究的重要方法，它可以获得被研究材料的多种电学信息。对于某种被研究的材料，可用交流电桥测出它在各种频率下的复阻抗，在复平面上以实部Zr（电阻）为横坐标，虚部的负值Zi（容抗）为纵坐标作图，称为复阻抗谱。然后，对此复阻抗谱进行分析和讨论。

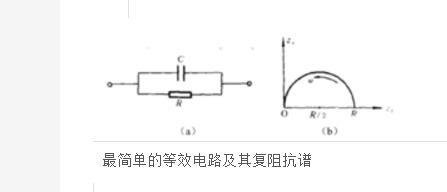
　　被研究材料的电学性质常常比较复杂。为了简化，常采用某种等效电路进行模拟。例如，上图所示是最简单的等效电路，它的复阻抗谱是一个半圆，圆心在（R/2，0），半径为R/2。于是，由实验测定的复阻抗谱即可求得材料的直流体电阻R值。

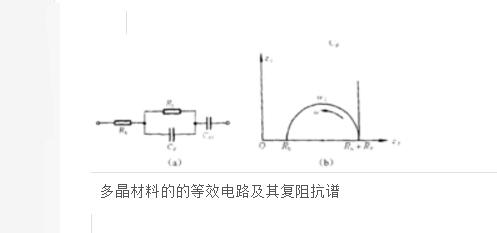
　　实际情况并不是如此简单。例如，用不可逆电极测量多晶固体电解质，其等效电路一般应如上图所示，图中Rb为晶粒体电阻，Rp和Cp为晶粒间界电阻和电容，Cdl为电极双电层电容。此种等效电路的复阻抗谱由一个半圆和一条直线构成。在半圆的顶点上，有ω1CpRp=1，此处ω1为顶点对应的频率。半圆在横坐标上的截距为Rb和Rb+Rp。因此，由实验测得的复阻抗谱即可求出晶粒的体电阻Rb、晶粒间界的电阻Rp和电容Cp等与材料性质有关的物理量。

　　仿此，对材料的复导纳也可作类似处理，得到复导纳谱。人们也常用复导纳谱研究材料的电学性质。

　　阻抗的概念

　　在具有电阻、电感和电容的电路里，对电路中的电流所起的阻碍作用叫做阻抗。阻抗常用Z表示，是一个复数，实际称为电阻，虚称为电抗，其中电容在电路中对交流电所起的阻碍作用称为容抗，电感在电路中对交流电所起的阻碍作用称为感抗，电容和电感在电路中对交流电引起的阻碍作用总称为电抗。阻抗的单位是欧姆。阻抗的概念不仅存在与电路中，在力学的振动系统中也有涉及。

　　阻抗是表示元件性能或一段电路电性能的物理量。交流电路中一段无源电路两端电压峰值（或有效值）Um与通过该电路电流峰值（或有效值）Im之比称为阻抗，用z表示，单位为欧姆（Ω）。在U一定的情况下，z越大则I越小，阻抗对电流有限制的作用。

　　阻抗公式

　　Z=R+i（ωL–1/（ωC））

　　说明：负载是电阻、电感的感抗、电容的容抗三种类型的复物，复合后统称“阻抗”，写成数学公式即是：阻抗Z=R+i（ωL–1/（ωC））。其中R为电阻，ωL为感抗，1/（ωC）为容抗。

　　（1）如果（ωL–1/ωC）》0，称为“感性负载”；

　　（2）反之，如果（ωL–1/ωC）《0称为“容性负载”。

　　阻抗和复阻抗有什么区别

　　阻抗是复阻抗的大小。

　　阻抗不是相量，其大小为Z=√（R²+X²）。当只需要计算电流大小的时候，用阻抗即可。

　　复阻抗是相量，它不但有大小，还有幅角（即阻抗角φ，又是功率因数角），φ=arctgX/R。当需要考虑电流电压的相位时，必须用复阻抗。