堆和堆的应用：堆排序和优先队列

算法与数据结构 2018-03-16 3735

描述

1.堆

堆(Heap))是一种重要的数据结构，是实现优先队列(Priority Queues)首选的数据结构。由于堆有很多种变体，包括二项式堆、斐波那契堆等，但是这里只考虑最常见的就是二叉堆（以下简称堆）。

堆是一棵满足一定性质的二叉树，具体的讲堆具有如下性质：父节点的键值总是不大于它的孩子节点的键值（小顶堆）, 堆可以分为小顶堆和大顶堆，这里以小顶堆为例，其主要包含的操作有：

insert()

extractMin

peek(findMin)

delete(i)

由于堆是一棵形态规则的二叉树，因此堆的父节点和孩子节点存在如下关系：

设父节点的编号为 i, 则其左孩子节点的编号为2*i+1, 右孩子节点的编号为2*i+2设孩子节点的编号为i, 则其父节点的编号为(i-1)/2

由于二叉树良好的形态已经包含了父节点和孩子节点的关系信息，因此就可以不使用链表而简单的使用数组来存储堆。

要实现堆的基本操作，涉及到的两个关键的函数

siftUp(i, x) ：将位置i的元素x向上调整，以满足堆得性质，常常是用于insert后，用于调整堆；

siftDown(i, x)：同理，常常是用于delete(i)后，用于调整堆；

具体的操作如下：

privatevoidsiftUp(inti){

intkey = nums[i];

for(;i > 0;){

intp = (i - 1) >>> 1;

if(nums[p] <= key)

break;

nums[i] = nums[p];

i = p;

}

nums[i] = key;

}

privatevoidsiftDown(inti){

intkey = nums[i];

for(;i < nums.length / 2;){

intchild = (i << 1) + 1;

if(child + 1 < nums.length && nums[child] > nums[child+1])

child++;

if(key <= nums[child])

break;

nums[i] = nums[child];

i = child;

}

nums[i] = key;

}

可以看到siftUp和siftDown不停的在父节点和子节点之间比较、交换；在不超过logn的时间复杂度就可以完成一次操作。

有了这两个基本的函数，就可以实现上述提及的堆的基本操作。

首先是如何建堆，实现建堆操作有两个思路:

一个是不断地insert（insert后调用的是siftUp）

另一个将原始数组当成一个需要调整的堆，然后自底向上地在每个位置i调用siftDown(i)，完成后我们就可以得到一个满足堆性质的堆。这里考虑后一种思路：

通常堆的insert操作是将元素插入到堆尾，由于新元素的插入可能违反堆的性质，因此需要调用siftUp操作自底向上调整堆；堆移除堆顶元素操作是将堆顶元素删除，然后将堆最后一个元素放置在堆顶，接着执行siftDown操作，同理替换堆顶元素也是相同的操作。

建堆

// 建立小顶堆

privatevoidbuildMinHeap(int[]nums){

intsize = nums.length;

for(intj = size / 2 - 1;j >= 0;j--)

siftDown(nums,j,size);

}

那么建堆操作的时间复杂度是多少呢？答案是O(n)。虽然siftDown的操作时间是logn，但是由于高度在递减的同时，每一层的节点数量也在成倍减少，最后通过数列错位相减可以得到时间复杂度是O(n)。

extractMin由于堆的固有性质，堆的根便是最小的元素，因此peek操作就是返回根nums[0]元素即可；若要将nums[0]删除，可以将末尾的元素nums[n-1]覆盖nums[0],然后将堆得size = size-1，调用siftDown(0)调整堆。时间复杂度为logn。

peek同上

delete(i)

删除堆中位置为i的节点，涉及到两个函数siftUp和siftDown，时间复杂度为logn,具体步骤是，

将元素last覆盖元素i，然后siftDown

检查是否需要siftUp

注意到堆的删除操作，如果是删除堆的根节点，则不用考虑执行siftUp的操作；若删除的是堆的非根节点，则要视情况决定是siftDown还是siftUp操作，两个操作是互斥的。

publicintdelete(inti){

intkey = nums[i];

//将last元素移动过来，先siftDown; 再视情况考虑是否siftUp

intlast = nums[i] = nums[size-1];

size--;

siftDown(i);

//check #i的node的键值是否确实发生改变（是否siftDown操作生效）,若发生改变，则ok,否则为确保堆性质，则需要siftUp

if(i < size && nums[i] == last){

System.out.println("delete siftUp");

siftUp(i);

}

returnkey;

}

case 1 :

删除中间节点i21，将最后一个节点复制过来；

由于没有进行siftDown操作，节点i的值仍然为6，因此为确保堆的性质，执行siftUp操作；

case 2

删除中间节点i，将值为11的节点复制过来，执行siftDown操作；

由于执行siftDown操作后，节点i的值不再是11，因此就不用再执行siftUp操作了，因为堆的性质在siftDown操作生效后已经得到了保持。

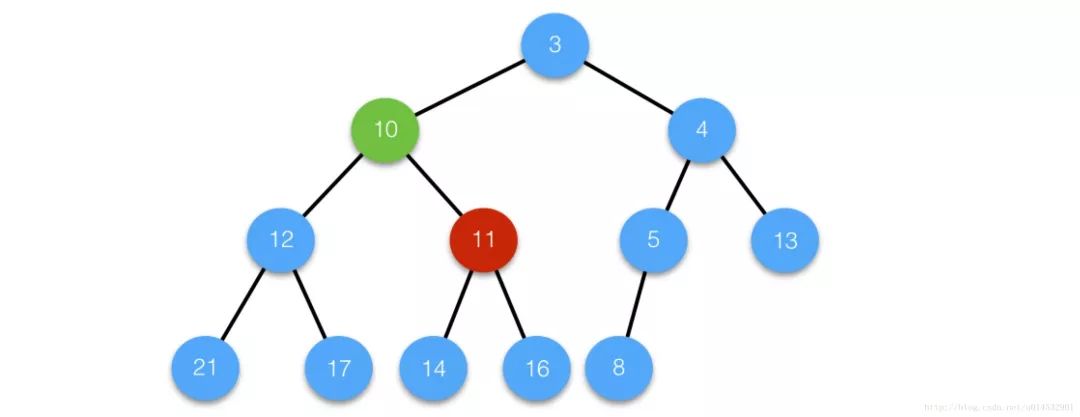
可以看出，堆的基本操作都依赖于两个核心的函数siftUp和siftDown；较为完整的Heap代码如下：

classHeap{

privatefinalstaticintN = 100;//default size

privateint[]nums;

privateintsize;

publicHeap(int[]nums){

this.nums = nums;

this.size = nums.length;

heapify(this.nums);

}

publicHeap(){

this.nums = newint[N];

}

/**

* heapify an array, O(n)

* @param nums An array to be heapified.

privatevoidheapify(int[]nums){

for(intj = (size - 1) >> 1;j >= 0;j--)

siftDown(j);

}

/**

* append x to heap

* O(logn)

* @param x

* @return

publicintinsert(intx){

if(size >= this.nums.length)

expandSpace();

size += 1;

nums[size-1] = x;

siftUp(size-1);

returnx;

}

/**

* delete an element located in i position.

* O(logn)

* @param i

* @return

publicintdelete(inti){

rangeCheck(i);

intkey = nums[i];

//将last元素覆盖过来,先siftDown; 再视情况考虑是否siftUp;

intlast = nums[i] = nums[size-1];

size--;

siftDown(i);

//check #i的node的键值是否确实发生改变,若发生改变，则ok,否则为确保堆性质，则需要siftUp;

if(i < size && nums[i] == last)

siftUp(i);

returnkey;

}

/**

* remove the root of heap, return it's value, and adjust heap to maintain the heap's property.

* O(logn)

* @return

publicintextractMin(){

rangeCheck(0);

intkey = nums[0],last = nums[size-1];

nums[0] = last;

size--;

siftDown(0);

returnkey;

}

/**

* return an element's index, if not exists, return -1;

* O(n)

* @param x

* @return

publicintsearch(intx){

for(inti = 0;i < size;i++)

if(nums[i] == x)

returni;

return -1;

}

/**

* return but does not remove the root of heap.

* O(1)

* @return

publicintpeek(){

rangeCheck(0);

returnnums[0];

}

privatevoidsiftUp(inti){

intkey = nums[i];

for(;i > 0;){

intp = (i - 1) >>> 1;

if(nums[p] <= key)

break;

nums[i] = nums[p];

i = p;

}

nums[i] = key;

}

privatevoidsiftDown(inti){

intkey = nums[i];

for(;i < size / 2;){

intchild = (i << 1) + 1;

if(child + 1 < size && nums[child] > nums[child+1])

child++;

if(key <= nums[child])

break;

nums[i] = nums[child];

i = child;

}

nums[i] = key;

}

privatevoidrangeCheck(inti){

if(!(0 <= i && i < size))

thrownewRuntimeException("Index is out of boundary");

}

privatevoidexpandSpace(){

this.nums = Arrays.copyOf(this.nums,size *2);

}

@Override

publicStringtoString(){

// TODO Auto-generated method stub

StringBuilder sb = newStringBuilder();

sb.append("[");

for(inti = 0;i < size;i++)

sb.append(String.format((i != 0?", " : "") + "%d",nums[i]));

sb.append("] ");

returnsb.toString();

}

2.堆的应用：堆排序

运用堆的性质，我们可以得到一种常用的、稳定的、高效的排序算法————堆排序。堆排序的时间复杂度为O(n*log(n))，空间复杂度为O(1)，堆排序的思想是：对于含有n个元素的无序数组nums, 构建一个堆(这里是小顶堆)heap，然后执行extractMin得到最小的元素，这样执行n次得到序列就是排序好的序列。如果是降序排列则是小顶堆；否则利用大顶堆。

Trick

由于extractMin执行完毕后，最后一个元素last已经被移动到了root，因此可以将extractMin返回的元素放置于最后，这样可以得到sort in place的堆排序算法。

具体操作如下：

int[]n = newint[]{1,9,5,6,8,3,1,2,5,9,86};

Heaph = newHeap(n);

for(inti = 0;i < n.length;i++)

n[n.length-1-i] = h.extractMin();

当然，如果不使用前面定义的heap，则可以手动写堆排序，由于堆排序设计到建堆和extractMin，两个操作都公共依赖于siftDown函数，因此我们只需要实现siftDown即可。(trick:由于建堆操作可以采用siftUp或者siftDown，而extractMin是需要siftDown操作，因此取公共部分，则采用siftDown建堆)。

这里便于和前面统一，采用小顶堆数组进行降序排列。

publicvoidheapSort(int[]nums){

intsize = nums.length;

buildMinHeap(nums);

while(size != 0){

// 交换堆顶和最后一个元素

inttmp = nums[0];

nums[0] = nums[size - 1];

nums[size - 1] = tmp;

size--;

siftDown(nums,0,size);

}

// 建立小顶堆

privatevoidbuildMinHeap(int[]nums){

intsize = nums.length;

for(intj = size / 2 - 1;j >= 0;j--)

siftDown(nums,j,size);

}

privatevoidsiftDown(int[]nums,inti,intnewSize){

intkey = nums[i];

while(i < newSize >>> 1){

intleftChild = (i << 1) + 1;

intrightChild = leftChild + 1;

// 最小的孩子，比最小的孩子还小

intmin = (rightChild >= newSize || nums[leftChild] < nums[rightChild])?leftChild : rightChild;

if(key <= nums[min])

break;

nums[i] = nums[min];

i = min;

}

nums[i] = key;

}

3.堆的应用：优先队列

优先队列是一种抽象的数据类型，它和堆的关系类似于，List和数组、链表的关系一样；我们常常使用堆来实现优先队列，因此很多时候堆和优先队列都很相似，它们只是概念上的区分。优先队列的应用场景十分的广泛：常见的应用有：

Dijkstra’s algorithm（单源最短路问题中需要在邻接表中找到某一点的最短邻接边，这可以将复杂度降低。）

Huffman coding（贪心算法的一个典型例子，采用优先队列构建最优的前缀编码树(prefixEncodeTree)）

Prim’s algorithm for minimum spanning tree

Best-first search algorithms

这里简单介绍上述应用之一：Huffman coding。

Huffman编码是一种变长的编码方案，对于每一个字符，所对应的二进制位串的长度是不一致的，但是遵守如下原则：

出现频率高的字符的二进制位串的长度小

不存在一个字符c的二进制位串s是除c外任意字符的二进制位串的前缀

遵守这样原则的Huffman编码属于变长编码，可以无损的压缩数据，压缩后通常可以节省20%-90%的空间，具体压缩率依赖于数据的固有结构。

Huffman编码的实现就是要找到满足这两种原则的字符-二进制位串对照关系，即找到最优前缀码的编码方案（前缀码：没有任何字符编码后的二进制位串是其他字符编码后位串的前缀）。这里我们需要用到二叉树来表达最优前缀码，该树称为最优前缀码树一棵最优前缀码树看起来像这样：

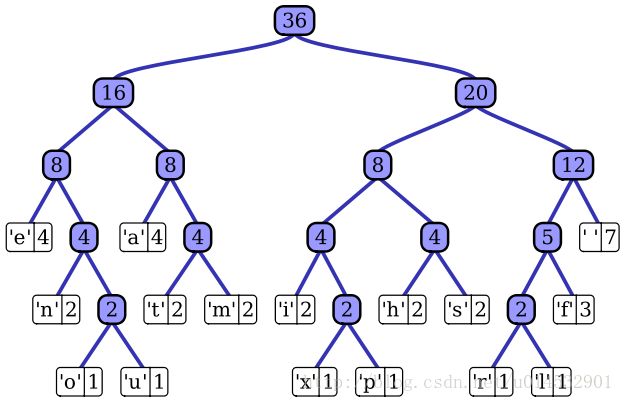
算法思想：用一个属性为freqeunce关键字的最小优先队列Q,将当前最小的两个元素x,y合并得到一个新元素z（z.frequence = x.freqeunce + y.frequence）,然后插入到优先队列中Q中，这样执行n-1次合并后，得到一棵最优前缀码树（这里不讨论算法的证明）。

一个常见的构建流程如下：

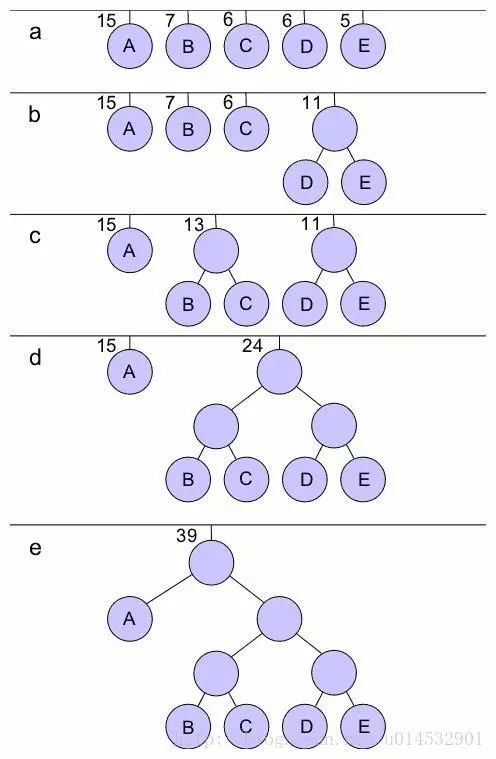
树中指向某个节点左孩子的边上表示位0,指向右孩子的边上的表示位1，这样遍历一棵最优前缀码树就可以得到对照表。

import java.util.Comparator;

import java.util.HashMap;

import java.util.Map;

import java.util.PriorityQueue;

/**

* root

* /

* --------- ----------

* |c:freq | | c:freq |

* --------- ----------

publicclassHuffmanEncodeDemo{

publicstaticvoidmain(String[]args){

// TODO Auto-generated method stub

Node[]n = newNode[6];

float[]freq = newfloat[]{9,5,45,13,16,12};

char[]chs = newchar[]{'e','f','a','b','d','c'};

HuffmanEncodeDemo demo = newHuffmanEncodeDemo();

Node root = demo.buildPrefixEncodeTree(n,freq,chs);

Map collector = newHashMap<>();

StringBuilder sb = newStringBuilder();

demo.tranversalPrefixEncodeTree(root,collector,sb);

System.out.println(collector);

Strings = "abcabcefefefeabcdbebfbebfbabc";

StringBuilder sb1 = newStringBuilder();

for(charc : s.toCharArray()){

sb1.append(collector.get(c));

}

System.out.println(sb1.toString());

}

publicNode buildPrefixEncodeTree(Node[]n,float[]freq,char[]chs){

PriorityQueue pQ = newPriorityQueue<>(newComparator(){

publicintcompare(Node o1,Node o2){

returno1.item.freq > o2.item.freq?1 : o1.item.freq == o2.item.freq?0 : -1;

};

});

Nodee = null;

for(inti = 0;i < chs.length;i++){

n[i] = e = newNode(null,null,newItem(chs[i],freq[i]));

pQ.add(e);

}

for(inti = 0;i < n.length - 1;i++){

Nodex = pQ.poll(),y = pQ.poll();

Nodez = newNode(x,y,newItem('$',x.item.freq + y.item.freq));

pQ.add(z);

}

returnpQ.poll();

}

/**

* tranversal

* @param root

* @param collector

* @param sb

publicvoidtranversalPrefixEncodeTree(Node root,Map collector,StringBuilder sb){

// leaf node

if(root.left == null && root.right == null){

collector.put(root.item.c,sb.toString());

return;

}

Node left = root.left,right = root.right;

tranversalPrefixEncodeTree(left,collector,sb.append(0));

sb.delete(sb.length() - 1,sb.length());

tranversalPrefixEncodeTree(right,collector,sb.append(1));

sb.delete(sb.length() - 1,sb.length());

}

classNode{

publicNode left,right;

publicItem item;

publicNode(Node left,Node right,Item item){

super();

this.left = left;

this.right = right;

this.item = item;

}

classItem{

publiccharc;

publicfloatfreq;

publicItem(charc,floatfreq){

super();

this.c = c;

this.freq = freq;

}

输出如下：

{a=0,b=101,c=100,d=111,e=1101,f=1100}

010110001011001101110011011100110111001101010110011110111011011100101110110111001010101100

4 堆的应用：海量实数中（一亿级别以上）找到TopK（一万级别以下）的数集合。

A:通常遇到找一个集合中的TopK问题，想到的便是排序，因为常见的排序算法例如快排算是比较快了，然后再取出K个TopK数，时间复杂度为O(nlogn)，当n很大的时候这个时间复杂度还是很大的；

B:另一种思路就是打擂台的方式,每个元素与K个待选元素比较一次，时间复杂度很高：O(k*n)，此方案明显逊色于前者。

对于一亿数据来说，A方案大约是26.575424*n；

C:由于我们只需要TopK，因此不需要对所有数据进行排序，可以利用堆得思想，维护一个大小为K的小顶堆，然后依次遍历每个元素e, 若元素e大于堆顶元素root，则删除root，将e放在堆顶，然后调整，时间复杂度为logK；若小于或等于，则考察下一个元素。这样遍历一遍后，最小堆里面保留的数就是我们要找的topK，整体时间复杂度为O(k+n*logk)约等于O(n*logk)，大约是13.287712*n（由于k与n数量级差太多），这样时间复杂度下降了约一半。

A、B、C三个方案中，C通常是优于B的，因为logK通常是小于k的，当K和n的数量级相差越大，这种方式越有效。

以下为具体操作：

import java.io.File;

import java.io.FileNotFoundException;

import java.io.PrintWriter;

import java.io.UnsupportedEncodingException;

import java.util.Arrays;

import java.util.Scanner;

import java.util.Set;

import java.util.TreeSet;

publicclassTopKNumbersInMassiveNumbersDemo{

publicstaticvoidmain(String[]args){

// TODO Auto-generated method stub

int[]topK = newint[]{50001,50002,50003,50004,50005};

genData(1000 * 1000 * 1000,500,topK);

longt = System.currentTimeMillis();

findTopK(topK.length);

System.out.println(String.format("cost:%fs",(System.currentTimeMillis() - t) * 1.0 / 1000));

}

publicstaticvoidgenData(intN,intmaxRandomNumer,int[]topK){

Filef = newFile("data.txt");

intk = topK.length;

Set index = newTreeSet<>();

for(;;){

index.add((int)(Math.random() * N));

if(index.size() == k)

break;

}

System.out.println(index);

intj = 0;

try{

PrintWriter pW = newPrintWriter(f,"UTF-8");

for(inti = 0;i < N;i++)

if(!index.contains(i))

pW.println((int)(Math.random() * maxRandomNumer));

else

pW.println(topK[j++]);

pW.flush();

}catch(FileNotFoundExceptione){

// TODO Auto-generated catch block

e.printStackTrace();

}catch(UnsupportedEncodingExceptione){

// TODO Auto-generated catch block

e.printStackTrace();

}

publicstaticvoidfindTopK(intk){

int[]nums = newint[k];

//read

Filef = newFile("data.txt");

try{

Scanner scanner = newScanner(f);

for(intj = 0;j < k;j++)

nums[j] = scanner.nextInt();

heapify(nums);

//core

while(scanner.hasNextInt()){

inta = scanner.nextInt();

if(a <= nums[0])

continue;

else{

nums[0] = a;

siftDown(0,k,nums);

}

System.out.println(Arrays.toString(nums));

}catch(FileNotFoundExceptione){

// TODO Auto-generated catch block

e.printStackTrace();

}

//O(n), minimal heap

publicstaticvoidheapify(int[]nums){

intsize = nums.length;

for(intj = (size - 1) >> 1;j >= 0;j--)

siftDown(j,size,nums);

}

privatestaticvoidsiftDown(inti,intn,int[]nums){

intkey = nums[i];

for(;i < (n >>> 1);){

intchild = (i << 1) + 1;

if(child + 1 < n && nums[child] > nums[child+1])

child++;

if(key <= nums[child])

break;

nums[i] = nums[child];

i = child;

}

nums[i] = key;

}

ps:大致测试了一下，10亿个数中找到top5需要140秒左右，应该是很快了。

5 总结

堆是基于树的满足一定约束的重要数据结构，存在许多变体例如二叉堆、二项式堆、斐波那契堆（很高效）等。

堆的几个基本操作都依赖于两个重要的函数siftUp和siftDown，堆的insert通常是在堆尾插入新元素并siftUp调整堆，而extractMin是在删除堆顶元素，然后将最后一个元素放置堆顶并调用siftDown调整堆。

二叉堆是常用的一种堆，其是一棵二叉树；由于二叉树良好的性质，因此常常采用数组来存储堆。堆得基本操作的时间复杂度如下表所示：

heapify	insert	peek	extractMin	delete(i)
O(n)	O(logn)	O(1)	O(logn)	O(logn)

二叉堆通常被用来实现堆排序算法，堆排序可以sort in place，堆排序的时间复杂度的上界是O(nlogn)，是一种很优秀的排序算法。由于存在相同键值的两个元素处于两棵子树中，而两个元素的顺序可能会在后续的堆调整中发生改变，因此堆排序不是稳定的。降序排序需要建立小顶堆，升序排序需要建立大顶堆。

堆是实现抽象数据类型优先队列的一种方式，优先队列有很广泛的应用，例如Huffman编码中使用优先队列利用贪心算法构建最优前缀编码树。

堆的另一个应用就是在海量数据中找到TopK个数，思想是维护一个大小为K的二叉堆，然后不断地比较堆顶元素，判断是否需要执行替换对顶元素的操作，采用此方法的时间复杂度为n*logk，当k和n的数量级差距很大的时候，这种方式是很有效的方法。

6 references

[1] https://en.wikipedia.org/wiki/Heap_(data_structure))

[2] https://en.wikipedia.org/wiki/Heapsort

[3] https://en.wikipedia.org/wiki/Priority_queue

[4] https://www.cnblogs.com/swiftma/p/6006395.html

[5] Thomas H.Cormen, Charles E.Leiserson, Ronald L.Rivest, Clifford Stein.算法导论[M].北京:机械工业出版社,2015:245-249

[6] Jon Bentley.编程珠玑[M].北京:人民邮电出版社,2015:161-174

●本文编号591，以后想阅读这篇文章直接输入591即可

●输入m获取文章目录

打开APP阅读更多精彩内容