基于DBFP与DB-Attn的算法硬件协同优化方案

本文讨论了LLM推理过程对计算资源需求急剧攀升的背景下，现有量化和剪枝技术、新数据格式存在的不足，提出动态块浮点数（DBFP）及其配套算法-硬件协同框架DB-Attn以解决这些问题。

序言

近年来，以LLaMA和Mistral为代表的大型语言模型（Large Language Models, LLMs）在自然语言理解、生成和多模态任务中展现了革命性的能力。然而，随着模型规模的指数级增长，其推理过程对计算资源的需求急剧攀升，尤其体现在内存带宽占用和算力消耗上。

量化和剪枝技术通过减少模型的大小和计算复杂度，在一定程度上缓解了资源压力，但往往伴随着模型精度的显著下降，并且需要复杂的后训练过程。新的数据格式，如 BF16 和 TF32，相较于标准的 FP32 在计算成本上有所降低，但对于大规模、低成本的推理任务而言，仍然不够理想。

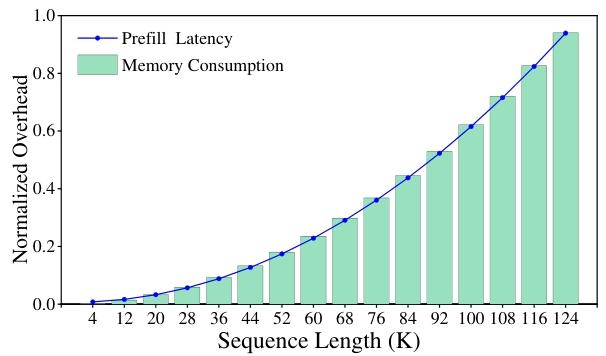
此外，大模型推理计算资源消耗的增幅与输入序列长度同样呈现显著相关性——当处理长文本序列时，非线性运算模块逐渐成为制约推理效率的关键瓶颈。具体而言，模型中广泛采用的Softmax、LayerNorm和GELU等非线性操作仍严重依赖标准浮点计算范式，导致计算效率显著低于线性运算模块。Softmax 层的计算时间在 LLMs 总推理时间中占比超过 30%，且 Attention 层的计算复杂度与输入长度呈二次方关系，导致随着序列长度增加，计算负担急剧加重。在 LLaMA3-8B 模型中，随着序列长度增长，内存消耗和延迟呈现超线性增长，严重影响了模型的推理效率。

块浮点（BFP）格式的出现为解决这些问题带来了新的思路。BFP 通过让一组定点数共享指数，将浮点运算转换为定点运算，在为 DNNs 推理提供广泛动态范围的同时，有效降低了硬件开销，在加速线性运算方面表现出显著优势。但目前 BFP 的研究主要集中在线性运算，在非线性运算领域的研究尚显不足。

块浮点数（Block Floating Point, BFP）作为一种高效数值表示格式，通过块内共享指数将浮点运算转换为定点运算，在GEMM（通用矩阵乘法）等线性操作中展现出显著优势。然而，现有BFP研究存在三大局限：

对齐策略僵化：传统BFP以块内最大值为对齐基准，导致小数值因过度右移而精度丢失，在Softmax中尤其致命；

分组机制固定：静态分组无法适应数据分布的动态变化，异常值（Outliers）易破坏块内数值对齐；

非线性支持不足：非线性操作需复杂函数计算（如指数、对数），但目前 BFP 的研究主要集中在线性运算，在非线性运算领域的研究尚显不足，同时现有BFP硬件设计缺乏相关针对性优化。

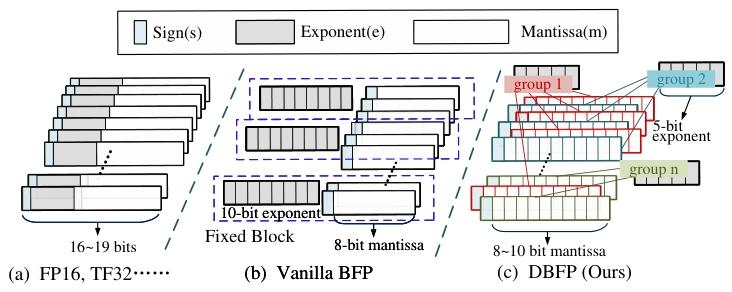
本文提出动态块浮点数（Dynamic-BFP, DBFP）及其配套算法-硬件协同框架DB-Attn，首次将BFP扩展至非线性操作领域。DBFP通过枢轴聚焦策略（Pivot-Focus Policy）和自适应分组策略（Adaptive Grouping Strategy）动态调整指数对齐方式，结合动态分层查找表（Dynamic Hierarchical LUT, DH-LUT）实现非线性函数的高效近似。硬件层面，设计基于RTL的DBFP引擎，支持FPGA与ASIC部署。实验表明，DB-Attn在LLaMA-7B的Softmax计算中实现74%的GPU加速，ASIC设计较SOTA方案性能提升10倍，同时模型精度损失可忽略（零样本任务平均下降<0.1%）。

相关工作

2.1 面向LLM的数据格式优化

主流低精度格式可分为三类：

BF16 格式采用 16 位表示，其中 8 位用于指数，7 位用于尾数，在一定程度上减少了存储和计算开销，适用于一些对精度要求不是极高的深度学习任务。TF32 格式是 NVIDIA 在 A100 GPU 中引入的 19 位浮点格式，结合了 FP32 的动态范围和 BF16 的计算效率，在深度学习计算中表现出较好的性能，但其硬件计算单元仍需浮点逻辑，功耗较高。

低比特定点数据类型，如 INT4，通过固定浮点比特数将运算转换为整数运算，计算效率较高，但在处理大动态范围数据时，由于精度有限，容易导致模型性能下降。

幂次量化格式通过将乘法运算替换为移位操作来简化计算，在某些场景下提高了计算速度，但这种格式在处理复杂数值计算时存在局限性，无法灵活适应各种计算需求。

BFP通过块内共享指数，在动态范围与计算效率间取得平衡。然而，现有BFP方案存在两大缺陷：其一，静态分组策略对异常值敏感，导致块内对齐误差累积；其二，缺乏对非线性操作的适配，如Song等人设计的BFP加速器仅支持GEMM，Softmax仍需回退至FP32计算。

2.2 非线性操作加速算法

非线性操作的硬件优化集中于两类方法：

基于 LUT 的方法通过预先计算并存储函数值，在计算时直接查找对应结果，具有较高的准确性。在 Softmax 运算中，可使用 LUT 存储指数函数的计算结果，加快运算速度。然而，这种方法需要大量存储空间来存储查找表，当函数输入范围较大或精度要求较高时，存储开销会显著增加。

近似算法通过对复杂函数进行近似计算来提高计算效率，使用多项式逼近或其他近似方法来计算非线性函数。随着计算单元的增大，近似算法的准确性通常会有所提高，但计算复杂度也会相应增加，并且在某些情况下可能会引入较大的误差。

基于 LUT 的方法通过预先计算并存储函数值，在计算时直接查找对应结果，具有较高的准确性。在 Softmax 运算中，可使用 LUT 存储指数函数的计算结果，加快运算速度。然而，这种方法需要大量存储空间来存储查找表，当函数输入范围较大或精度要求较高时，存储开销会显著增加。

近似算法通过对复杂函数进行近似计算来提高计算效率，使用多项式逼近或其他近似方法来计算非线性函数。随着计算单元的增大，近似算法的准确性通常会有所提高，但计算复杂度也会相应增加，并且在某些情况下可能会引入较大的误差。

当前方案在精度与效率间难以兼顾：LUT需要高容量SRAM存储，而多项式近似在非线性区域误差显著。DB-Attn通过DH-LUT实现动态非均匀分区，结合DBFP的共享指数特性，显著降低存储需求。

本文工作

3.1 动态块浮点数（Dynamic Block Floating-Point, DBFP）

DBFP的核心目标是优化传统BFP在非线性操作中的局限性。传统BFP将一组数据共享一个指数e8，通过将各元素的指数对齐至块内最大值emax，将浮点运算转换为定点运算。然而，这种对齐方式导致小数值的尾数因过度右移而精度丢失，公式化表示为：

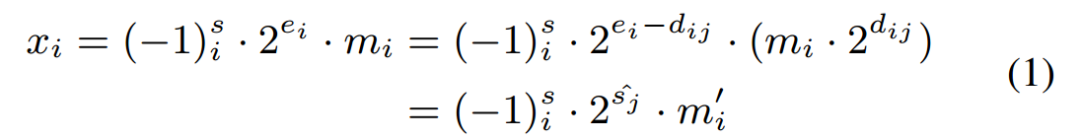
其中，dij= ei − 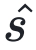j 表⽰ xi 的指数与第 j 个共享指数之间的差值。由于尾数与 2dij 相乘（移位 dij 位）时的有限精度，这种对⻬⽅式会引⼊误差。该误差取决于距离 dij，⽽ dij 由输⼊指数 ei 决定。当 ei = emax 时，⼩数值的 dij 较⼤，尾数有效位被截断，误差显著。

在 BFP 的基础上，DBFP 对其进⾏了进⼀步的优化。BFP 将⼀组数据表⽰为共享指数和私有尾数的形式，⽽ DBFP 则更加灵活地确定共享指数和分组⽅式。通过对数据分布的分析，DBFP 选择更具代表性的值，如中位数，作为对⻬枢轴，⽽不是像传统 BFP 那样使⽤最⼤值。这种枢轴聚焦策略能够更好地平衡数据的准确性，减少因异常值导致的精度损失。在 Softmax 运算的实验中，传统 BFP 以最⼤值为对⻬⽅向导致的损失⽐以中位数为对⻬⽅向⾼出 9.6 倍。

为了减少异常值对指数共享的影响，DBFP 引⼊了⾃适应分组策略。通过对数据的分析，将具有相似数量级分布的元素划分为⼀组，使得同⼀组内元素的指数差异较⼩，从⽽减少了因指数对⻬⽽产⽣的⽐特移位，降低了计算误差。在处理包含异常值的数据时，⾃适应分组策略能够将异常值单独处理，避免其对其他数据的指数共享产⽣过⼤影响。

DBFP数学优化⽬标定义为：

其中表⽰向量空间中从原点到点的⽅向和⼤⼩的向量。移位向量

决定了每个xi相对于共享指数的移位量。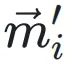和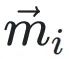分别表⽰转换前后尾数的投影，它们的欧⼏⾥得距离为

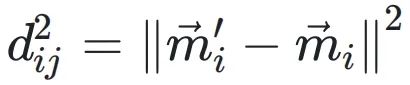
。μij表⽰xi落在由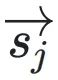定义的区间内的置信度。

在公式2中，超参数β（默认值为2）⽤于调节μij的重要程度。为了减轻异常值对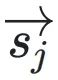选择的影响，引⼊了⼀个空集来处理这些异常值，μi0表⽰异常值属于该空集的置信度。异常值与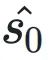之间的距离记为δ2，D2ij与所有Sj的距离总和相关，其定义为：

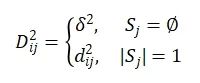
通过交替固定变量并求解约束最小化问题，得到了最优的共享指数集合，从而实现了自适应分组策略和枢轴聚焦策略的优化。

3.2 DB-Attn算法设计

DB-Attn是基于DBFP的软硬件协同优化框架，旨在提高Attention层的计算效率。该框架通过优化Softmax运算和矩阵运算，充分利用DBFP的特性，减少了浮点运算的需求，提高了计算吞吐量。

3.2.1 DH-LUT

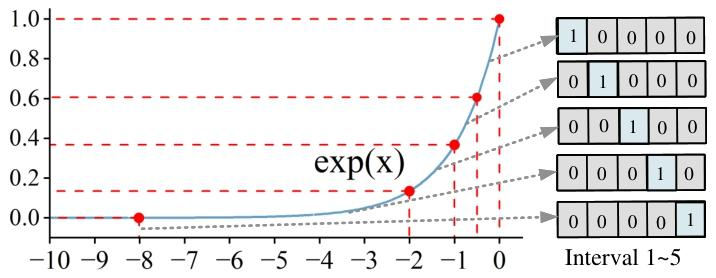
为了优化Softmax运算，DB-Attn提出了动态分层查找表（DH-LUT）算法。DH-LUT是一种紧凑、轻量级的LUT，它根据DBFP数据的共享指数动态加载子LUT，并利用尾数的高k位进行查找。

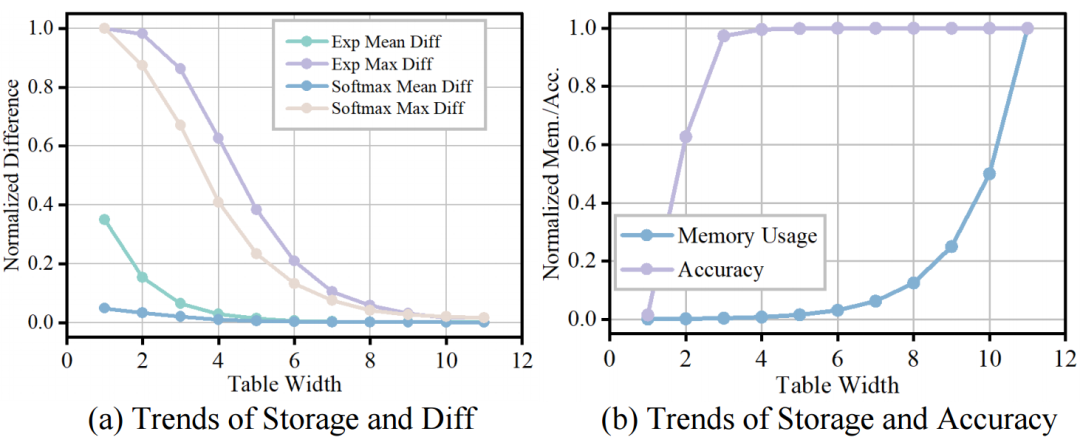
对于Softmax中的指数函数，DH-LUT仅对[-∞, 0]范围进行拟合，因为在Softmax的计算中，通过对指数进行降尺度变换（如 ex−xmax），数据主要集中在该范围内。DH-LUT支持非均匀拟合，通过在枢轴聚焦策略下对齐指数，能够更好地保留较小的值，并聚焦于函数的非线性显著部分。为了进一步优化DH-LUT的准确性和内存使用，设计了一种非均匀分层分配方法，根据目标拟合函数自适应地确定最优分区点，将更多的表项分配给非线性区域，以实现更精确的逼近。

基于DH-LUT的Softmax计算选择以中位数指数为对齐方式，能够在保证准确性的同时，平衡计算效率。由于DH-LUT中存储的数据均为DBFP格式，其共享指数的特性使得计算不仅可以在浮点域进行，还可以在计算资源有限的设备上进行整数运算，从而提高了Softmax算法在不同平台上的适用性和计算速度。

3.2.2 级联矩阵乘法优化

将DBFP应用于Attention中的矩阵运算，能够显著提高计算效率。在DBFP格式下，向量可以表示为共享系数和整数向量的乘积，向量点积和矩阵乘法可以通过整数乘法单元和整数加法器实现，避免了复杂的浮点运算。两个DBFP格式的向量

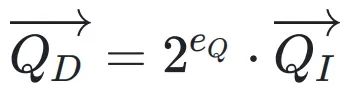
和

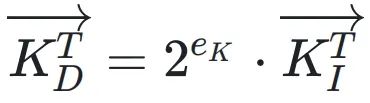
进行点积运算时，结果为

，可以通过整数运算高效实现。

这种特性使得DBFP矩阵乘法具有级联效应，即两个DBFP矩阵相乘的结果仍然是DBFP矩阵，可以无缝地连接进行后续的矩阵乘法运算，而无需额外的处理。对于细粒度块的DBFP矩阵，在级联运算中可以通过硬件移位操作高效地进行重新对齐，进一步提高了计算效率。

3.3 算法驱动的硬件架构

为了支持DB-Attn算法，我们设计并实现了一种基于RTL级的DBFP引擎，该引擎适用于FPGA和ASIC，能够有效提高Softmax运算的硬件性能。

该加速器的架构分为四个流水线阶段：

Max阶段：定位输入向量中的最大值xmax，为后续指数对齐提供基准；

SE阶段（Shared Exponent）：

￮ 根据枢轴策略计算共享指数es，并对齐尾数；

￮ 触发DMA预加载DH-LUT中对应区间的数据；

Exp阶段：

￮ 并行查表计算；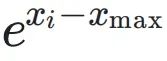

￮ 使用加法树累加分母和；

Div阶段：将分子与分母和相除，完成归一化。

采用动态分层非均匀LUT策略，通过从向量元素中提取 n 位创建一个 2n 项的表，在保证准确性的同时，有效控制了表的大小。该设计使用两个表：一个值表用于存储近似的指数值，一个命中位图表用于记录尾数的出现情况。输入向量可以并行地在这两个表中进行查找，每个指数索引对应一个DH-LUT区间，并设置相应的位图位。通过加法树结构对两个表的值进行相乘和求和，实现了并行查找结果，且无需额外的硬件资源。

DBFP能够将浮点运算转换为整数运算，这是其在硬件计算中的关键优势。在神经网络的向量加法运算中，传统的浮点加法需要对每对数字进行指数对齐，而DB-Attn通过在组内预对齐指数，将运算简化为指数乘法和尾数加法。在加法树结构中，通过一次初始的指数对齐，就可以直接进行尾数计算，实验证明，在4级加法树中，使用DBFP可以将延迟降低42%。

在非线性运算中，除法操作通常是并行计算的瓶颈，如在Softmax和Layernorm中。DBFP的共享指数特性使得可以通过整数近似高效地进行除法运算。传统的FP16串行除法器资源消耗大，10位尾数计算需要11个周期的移位操作，占用了超过90%的面积和功耗。而基于DBFP的除法器策略借鉴了相关的研究成果，使用LUT和移位加法操作，将11个周期的操作压缩为1个周期，大大提高了计算速度。在Softmax应用中，当除数固定且DBFP指数相同时，每64次除法仅需进行一次指数减法和查找操作，显著降低了资源利用率和延迟，实验证明，该除法单元能够将延迟降低83%。通过这些优化，DBFP使得FP16运算可以仅使用10位整数运算实现，有效降低了计算开销，特别有利于对比特宽度敏感的乘法和除法运算。

评估

4.1 DB-Attn 的准确性结果

4.1.1 LLM任务

在语言生成任务和六个零样本任务中，对 DB-Attn 的准确性进行了评估，并与传统的 BFP 和 FP8 格式进行了比较。以 LLaMA 系列模型为例，直接将传统 BFP 格式应用于 Softmax 操作会导致显著的准确性下降，如 LLaMA3 在零样本任务上的平均准确率下降了 33.81%。FP8 e4m3 格式由于无法表示无穷大，在 Attention 计算中表现不佳。而 DB-Attn 在所有评估任务中均优于传统 BFP 和 FP8 格式，能够保持与浮点运算几乎相同的准确性。在不同的数据集上，如 PIQA、ARC 等，DB-Attn 的零样本困惑度与浮点运算结果相近，证明了其在保持模型性能的同时，能够有效降低计算开销的优势。

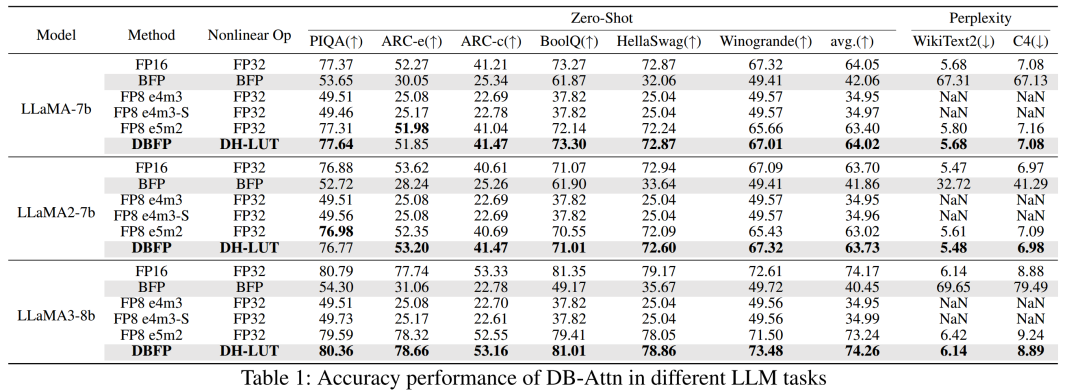
4.1.2 视觉任务

在目标检测和图像分类任务中，评估了 DB-Attn 的性能。使用流行的 ViT 和 Swin 骨干网络在 ImageNet 数据集上进行图像分类实验，以及利用 Detr 在 COCO 数据集上进行目标检测实验。结果表明，DB-Attn 的性能与在 LLMs 任务中的表现相似，能够无损地集成到现有的 Transformer 模型中，展示了其在不同任务和数据分布上的泛化性和通用性。在不同模型和数据集上，DB-Attn 的准确率与浮点运算相当，证明了其在视觉任务中的有效性。

4.1.3 DH-LUT 比特精度 - 准确率帕累托前沿

通过测试 DB-Attn 中 Softmax 在不同 LUT 比特宽度下的计算误差、LUT 内存使用和实际模型准确性，寻找 LUT 比特宽度配置的帕累托前沿。实验结果表明，当 LUT 比特宽度在 5 - 7 之间时，能够在计算误差、内存使用和准确性之间实现较好的平衡。在这个范围内，随着 LUT 比特宽度的增加，计算误差逐渐减小，模型准确性逐渐提高，但内存使用也会相应增加。通过合理选择 LUT 比特宽度，可以在保证模型性能的前提下，优化计算资源的使用。

4.2 硬件实现评估

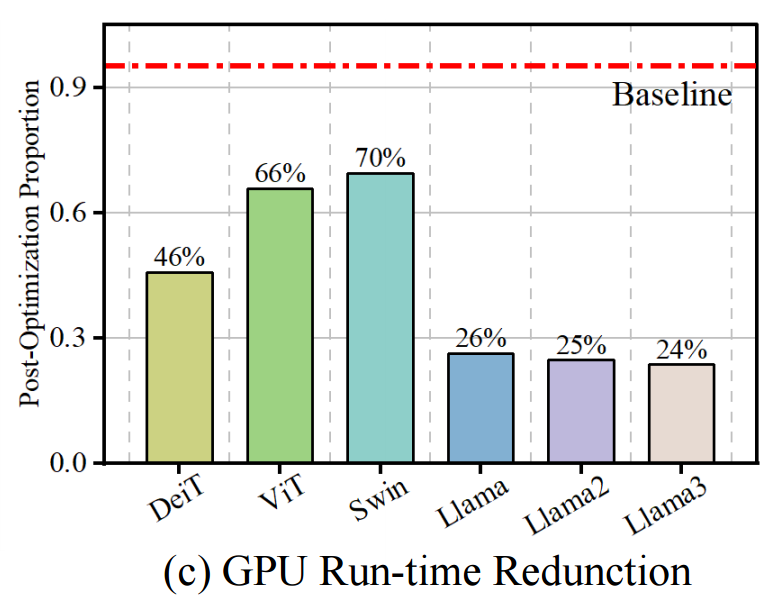
在NVIDIA A800 GPU上实现了自定义的CUDA Softmax算子来模拟DBFP格式，并在多种模型（如LLaMA和ViT）上进行推理。结果显示，基于DBFP的Softmax在不同模型架构上均实现了至少30%的速度提升，在LLaMA系列模型上平均延迟降低了74%。这表明DBFP能够有效加速Softmax运算，提高模型的推理效率。

在FPGA上对设计进行了评估，并与当前最先进的设计进行了比较。评估指标包括Softmax操作的处理延迟、FPGA资源利用率（以LUT和触发器FF为指标）、最大可实现的工作频率以及综合性能指标FOM（定义为

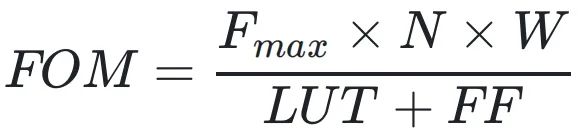
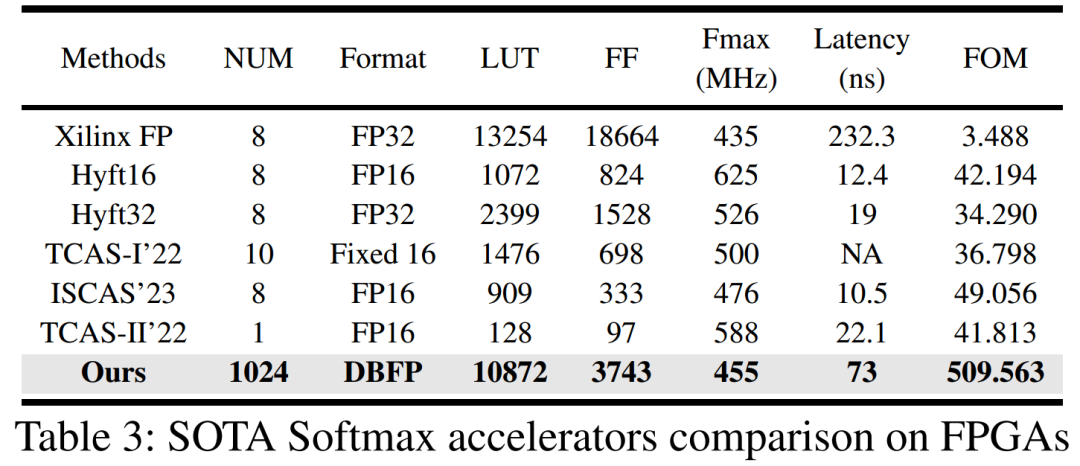
，其中W和N分别表示输入的精度和数量，FOM值越高表示性能越好）。与现有Softmax加速器相比，本文设计能够适应更大的输入带宽，在输入序列长度为1024（现代LLMs常用的设置）的情况下，使用的资源比Xilinx FP少54.21%，处理延迟降低了62.5%，计算带宽提高了128倍，FOM值提高了至少10倍，充分展示了DBFP在FPGA硬件实现上的优势。

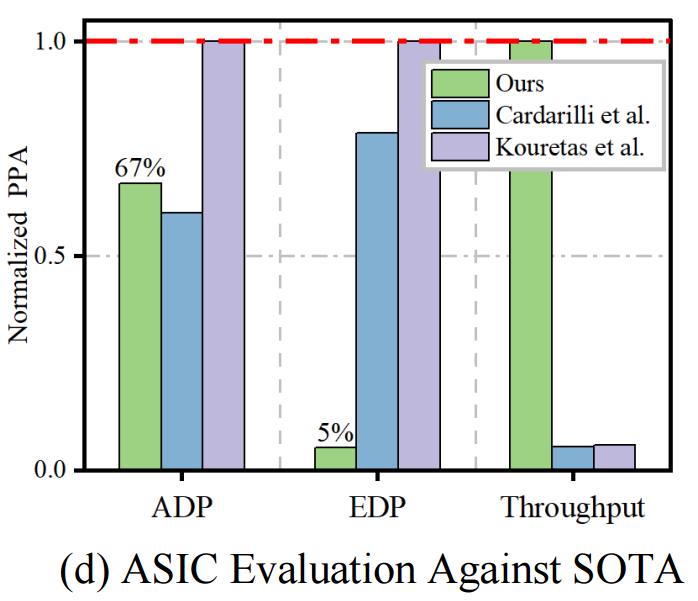
在ASIC上进行了实现，以获得更准确的功耗、最大时钟频率和可扩展性数据。使用面积 - 延迟积（ADP）、能量 - 延迟积（EDP）、整体效率和吞吐量（Freq × Bandwidth）等指标对设计进行评估。在输入序列长度为1024的统一场景下，将实验结果归一化到28nm工艺。与最先进的设计相比，本文设计虽然面积增加了约10%，但在能耗和吞吐量方面有显著提升，超过10倍。这表明在实际应用中，虽然需要额外的面积，但可以通过性能和效率的大幅提升来弥补，这种权衡是可接受的。

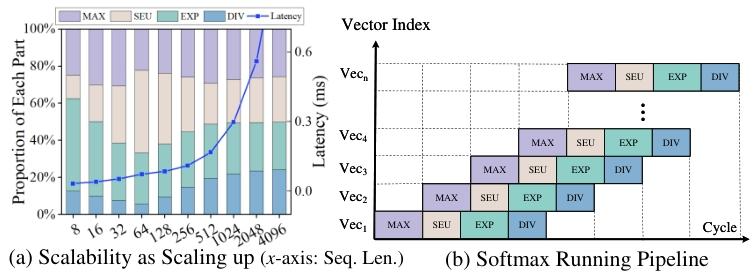
通过对输入大小从8到4096元素的调优测试，验证了设计的可扩展性。随着输入数据点数量的增加，总计算时间呈指数增长，这是由于输入长度与处理矩阵大小的二次关系。在输入大小增加的过程中，各个流水线阶段的时间消耗比例增长平衡，没有出现某个部分延迟增长过快的情况，证明了设计在处理大规模数据时的并行性和可扩展性，能够适应不同规模的应用需求。

总结

本文提出了 DBFP，一种先进的 BFP 变体，通过自适应分组和枢轴聚焦策略，有效解决了非线性运算中准确性和效率的挑战。在此基础上，构建了 DB-Attn 框架，通过算法和硬件的协同设计，实现了高效的 Attention 计算。实验结果表明，DB-Attn 在 GPU 上实现了 74% 的加速，且精度损失可忽略不计，基于 RTL 级的 DBFP 引擎比现有最先进的设计性能提升了 10 倍。

本文的研究成果为 BFP 在窄精度 LLM 推理中的应用开辟了新的道路，证明了软硬件协同设计在优化非线性运算方面的巨大潜力。未来的研究可以进一步探索 DB-Attn 在其他复杂神经网络结构和任务中的应用，以及如何进一步优化硬件架构，以降低成本和提高能效，推动 LLMs 在更广泛领域的高效应用。