一文看懂周期信号的频谱特点

周期信号概念

是周期信号瞬时幅值随时间重复变化的信号。常见的周期信号有：正弦信号、脉冲信号以及它们的整流、微分、积分等。这类可称为简单信号。它们的特点是在一个周期内的极值点不会超过两个且周期性特征明显。对于这类已明确具有周期特性的信号，周期与否的判别相对简单，周期测量的方法也很成熟完善，如：过零检测法，脉冲整形法等。

周期信号表达式

x（t）=x（t+kT），k=1，2.。。。。。

式中t表示时间，T表示周期。

　　频谱的概念

　　频谱是频率谱密度的简称，是频率的分布曲线。复杂振荡分解为振幅不同和频率不同的谐振荡，这些谐振荡的幅值按频率排列的图形叫做频谱。频谱广泛应用于声学、光学和无线电技术等方面。频谱将对信号的研究从时域引入到频域，从而带来更直观的认识。把复杂的机械振动分解成的频谱称为机械振动谱，把声振动分解成的频谱称为声谱，把光振动分解成的频谱称为光谱，把电磁振动分解成的频谱称为电磁波谱，一般常把光谱包括在电磁波谱的范围之内。分析各种振动的频谱就能了解该复杂振动的许多基本性质，因此频谱分析已经成为分析各种复杂振动的一项基本方法。

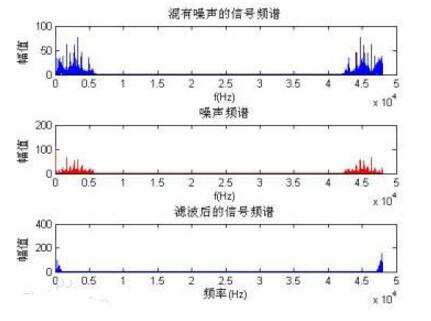
　　周期信号频谱的特点

　　（1）离散性：频谱谱线是离散的。

　　（2）收敛性：谐波幅值总的趋势随谐波次数的增加而降低。

　　（3）谐波性：谱线只出现在基频整数倍的频率处。

　　周期信号的有效频谱宽度

　　在周期信号的频谱分析中，周期矩形脉冲信号的频谱具有典型的意义，得到广泛的应用。下面以图3-8所示的周期矩形脉冲信号为例，进一步研究其频谱宽度与脉冲宽度之间的图3-8关系。

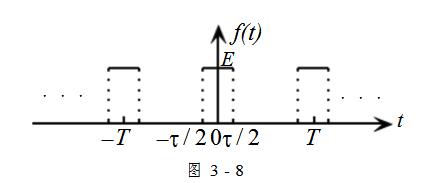
　　图3-8所示信号）（tf的脉冲宽度为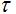，脉冲幅度为E，重复周期为T，重复角频率为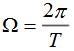

　　若将）（tf展开为式（3-17）傅里叶级数，则由式（3-18）可得

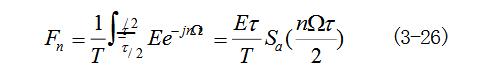
　　在这里Fn为实数。因此一般把振幅频谱和相位频谱合画在一幅图中，如图3-9所示

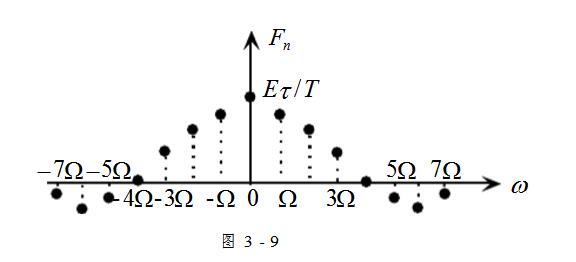
　　由此图可以看出：

　　（1）周期矩形脉冲信号的频谱是离散的，两谱线间隔为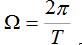

　　（2）直流分量、基波及各次谐波分量的大小正比于脉幅E和脉宽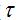，反比于周期T，其变化受包络线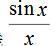的牵制。

　　（3）当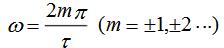时，谱线的包络线过零点。因此称为零分量频率。

　　（4）周期矩形脉冲信号包含无限多条谱线，它可分解为无限多个频率分量，但其主要能量集中在第一个零分量频率之内。因此通常把这段频率范围称为矩形信号的有效频谱宽度或信号的占有频带，记作或

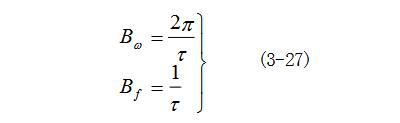
　　显然，有效频谱宽度B只与脉冲宽度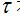有关，而且成反比关系。有效频谱宽度是研究信号与系统频率特性的重要内容，要使信号通过线性系统不失真，就要求系统本身所具有的频率特性必须与信号的频宽相适应。

　　对于一般周期信号，同样也可得到离散频谱，也存在零分量频率和信号的占有频带。

　　周期信号频谱与周期T的关系

　　下面仍以图3-8所示的周期矩形信号为例进行分析。因为

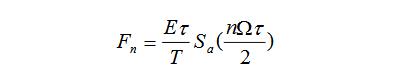
　　所以在脉冲宽度保持不变的情况下，若增大周期T，则可以看出：

　　（1）离散谱线的间隔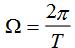将变小，即谱线变密。

　　（2）各谱线的幅度将变小，包络线变化缓慢，即振幅收敛速度变慢。

　　（3）由于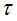不变，故零分量频率位置不变，信号有效频谱宽度亦不变。