信号无失真传输的条件_无失真传输的条件

　　什么是无失真传输

　　无失真传输是指只有幅度的大小与出现的时间先后不同，波形上没有变化的系统的输出信号或输入信号。

　　无失真传输条件

　　若要保持系统的无失真传输信号，从频域分析，可对式1两边取傅立叶变换，并利用其时移性，有

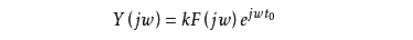
　　由于

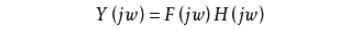
　　所以无失真传输的系统函数为（式2）

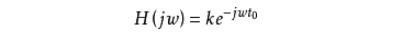
　　即

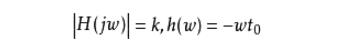
　　此，无失真传输系统在频域应满足两个条件：

　　（1）系统的幅频特性在整个频域范围内应为常数k，即系统的通频带为无穷大；

　　（2）系统的相频特性在整个频率范围内应与w成正比，即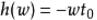，如图2所示。

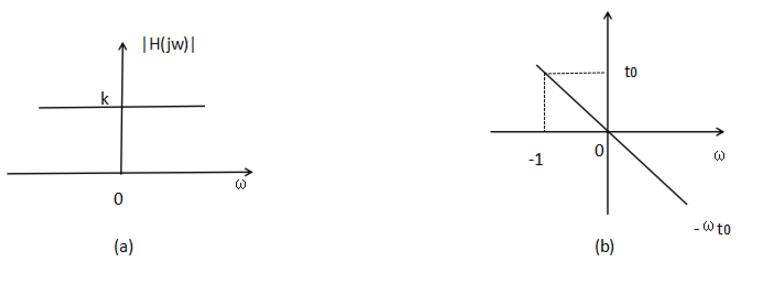
　　若对式2取傅立叶反变换，则可知系统的单位冲激响应为

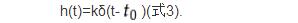
　　该式表明，一个无失真传输系统，其单位冲击响应仍为一个冲激函数，不过在强度上不一定为单位1，位置上也不一定位于t=0处。因此，式3从时域给出了无失真传输系统的条件。

　　无失真传输系统的幅频特性应在无限宽的频率范围内保持常量，这是不可能实现的。实际上，由于所有的信号其能量总是随频率的增高而减少，因此，系统只要有足够大的频宽，以保证包含绝大多数能量的频率分量能够通过，就可以获得较满意的传输质量。

　　线性系统引起的信号失真的原因

　　各频率分量幅度产生不同的衰减——幅度失真

　　各频率分量产生的相移不与频率成正比，响应的各频率分量在时间轴上的相对位置产生变化——相位失真

　　信号无失真传输的条件

　　时域条件：y（t）=kf（t-t0）或h（t）=kδ（t-t0）。

　　频域条件Y（jw）=kX（jw）e^（-jwt0）或H（jw）=ke^（-jwt0）。

　　时域是描述数学函数或物理信号对时间的关系。例如一个信号的时域波形可以表达信号随着时间的变化。若考虑离散时间，时域中的函数或信号，在各个离散时间点的数值均为已知。若考虑连续时间，则函数或信号在任意时间的数值均为已知。在研究时域的信号时，常会用示波器将信号转换为其时域的波形。

　　数字信号的无失真传输

　　为了研究波形传输的失真问题，我们首先来看一下基带信号传输系统的典型模型，如下图所示。在发送端，数字基带信号经发送滤波器输入到信道，发送滤波器的作用是限制发送频带，阻止不必要的频率成分干扰相邻信道。基带信号在信道中传输时常混入噪声，同时由于信道带宽的有限性，因此引起传输波形的失真是必然的。

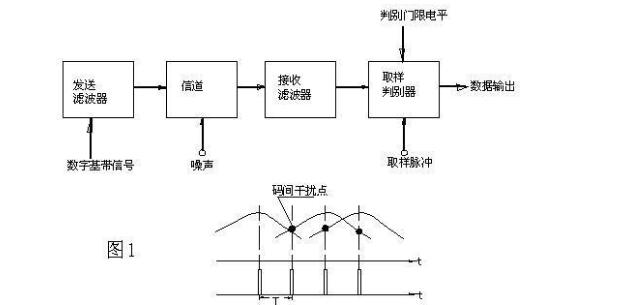
　　所以在接收端输入的波形与原始的基带信号肯定存在较大的差别，若直接进行抽样判决将会产生较大的误判。因此在抽样判决之前先经过一个接收滤波器，它一方面滤除带外噪声，另一方面对失真波形进行均衡。取样和判决电路使数字信号得到再生，并改善输出信号的质量。

　　根据频谱分析的基本原理，基带信号在频域上的失真，在时域上必定产生延伸，这就带来了各码元间相互串扰问题。所以，造成判决错误的主要原因除了噪声外，主要是由于传输特性（包括发、收滤波器和信道特性）不良引起的码间串扰。基带脉冲序列通过系统时，系统的滤波作用使脉冲拖宽（时域上的周期变长），在时间上，它们重叠到邻近时隙中去（如图1所示）。接收端在按约定的时隙对各点进行取样，并以取样时刻测定的信号幅度和判别门限电平进行比较，以此作为依据进行判决，来导出原脉冲的消息。若相邻脉冲的拖尾相加超过判别门限电平，则会使发送的“0”判为“1”。实际中可能出现好几个邻近脉冲的拖尾叠加，这种脉冲重叠，并在接收端造成判决困难的现象叫做码间干扰。

　　因此可以看出，传输基带信号受到约束的主要因素是系统的频率特性。当然可以有意地加宽传输频带使这种干扰减小到任意程度。然而这会导致不必要地浪费带宽。如果展宽得太多还会将过大的噪声引入系统。因此应该探索另外的代替途径，即通过设计信号波形，或采用合适的传输滤波器，以便在最小传输带宽的条件下大大减小或消除这种干扰。

　　奈奎斯特等人研究了以上的情况，提出了数字信号传输的无失真条件，称为奈奎斯特第一准则。其内容是，当数字信号序列通过某一信道传输时，如信号传输速率Bb=2Bc（Bc为信道物理带宽），各码元的间隔T=1/2Bc，该数字序列就可以做到无码间干扰传输了。这时Bc=1/2T称为奈奎斯特带宽，T称为奈奎斯特间隔。

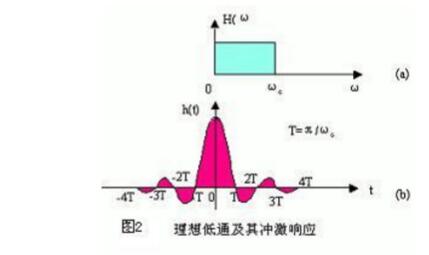
　　上面说过任何一个传输信道的带宽都时有限的，它的特性相当于一个低通滤波器。理想的低通滤波器的冲击响应为sinωct/ωct，其波形如图2b所示。如果传输的是二元数码序列，其频带利用率为Bb/Bc=2bit/s/Hz（式中Rb为传输码率，单位bps，BC是奈奎斯特带宽）。如果序列为n进制信号，则频带利用率

　　为2log2nbit/s/Hz（如16QAM24＝16所以是4进制的、64QAM26＝64所以是6进制的）。

　　奈奎斯特第一准则本质上是取样值无失真条件，它给我们指出了无码间干扰和充分利用频带的基本关系。同时说明信号经传输后，虽然整个波形会发生了变化，但只要取样值保持不变，那么再次取样的方法（即再生判决）仍然可以准确无误地恢复原始信号，为此，采用理想低通响应波形作接收是不会产生码间干扰的。

　　然而在实际中，理想的低通特性很难实现。这首先是因为理想低通特性在物理上不能实现，其次是它的冲击响应脉冲波形尾部的衰减振荡是比较大的，若定时的精确性稍微差一些，使取样瞬间出现偏差时，就会出现可观的码间干扰。

　　在实际应用中我们用的是具有滚降特性的信道。这种信道可以克服理想低通特性的两个缺点。

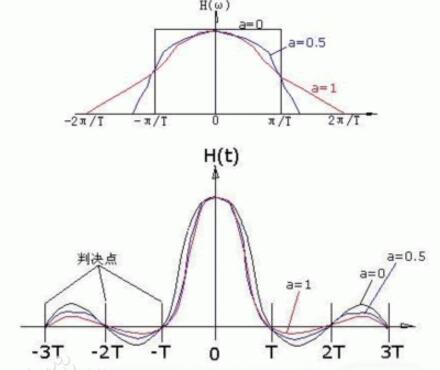
　　滚降特性信道其带宽较奈奎斯特带宽宽，增加的程度用滚降系数α来表示。a=fc2/fc1，a值的范围是0≤a≥1，式中的fc1是理想低通的截止频率，fc2滚降特性信道的截止频率。具有滚降系数a信道的特性和冲击响应如图3。

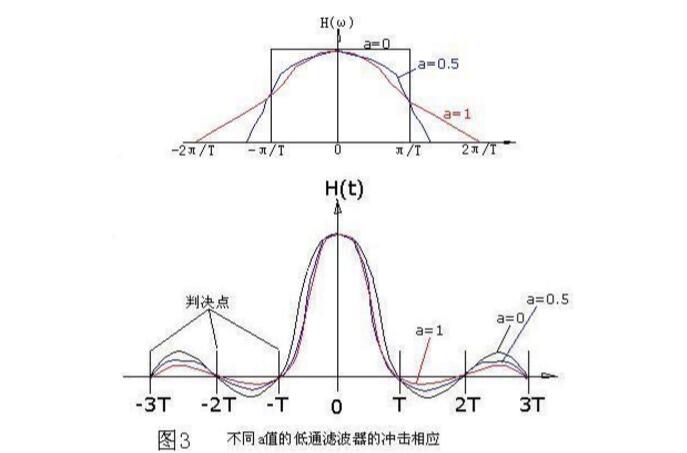
　　从上图中可看出：

　　1、当a＝0时，系统为理想低通特性，a≤1为升余弦滚降滤波特性。

　　2、对于a》0的升余弦滚降特性，其冲激响应H（t）的值，除在取样点

　　t=0处不为零外，其余各取样点的值均为零，且t》T后，各样值点之间又增加了一个零点，使“尾巴”随时间的延长而衰减加快。这对消除码间干扰和减弱定时抖动很有利。

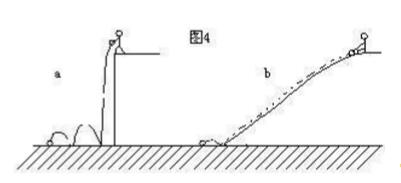
　　3、升余弦滚降信号在各取样点（图中的-3T、-2T、……。.2T、3T）处的串扰值始终为零，因此它满足取样值无失真传输条件。a越小，波形拖尾的振荡起伏越大，但传输所需要的带宽减少，即频带利用率高；反之，a越大，拖尾振荡起伏越小，传输所需要的带宽增大，即频带利用率变低，极限情况是a=1，此时的滚降特性所占带宽比a=0时增加一倍，这时其频带利用率只有极限情况下的一半。这种情况可以用图4来形象比如。图4a中的小球从峭壁中落下，到地后反弹幅度高且反弹时间长（拖尾长）。图4b中的小球从斜波上滚下，落地后反弹幅度很小且反弹时间短。

　　4、考虑到接收波形在再生判决中还再进行取样才能实现无失真传输，而在实际取样时，取样时刻不可能完全没有误差，加之取样脉冲宽度不可能为零，因此，为了减少取样定时的脉冲所带来的影响，a值不能取得太大，通常选择a0.16，例如在DVB-C系统中，调制前得I、Q信号，采用a=0.16的升余弦特性滤波。一个基于调制传输方式的计算例子，例如：a=0.16，使用64QAM调制，则频带利用率N=log264=6（每个调制符号的比特数），频道物理带宽为W=8MHz的DVB-C系统，求其有效传输速率SS，计算如下：

　　1、首先算其符号率D=W/（1+a）＝8/（1+0.16）=6.8966Ms/s

　　2、总传输速率C=D*N=6.8966*6=41.379Mbps

　　3、DVB-C的信道编码是RS（204，188），所以有效传输速率

　　CO=C*188/204=38.134Mbps

　　总的来说，由于传输信道存在抖动，所以，在判决时的定时不可能做到很精确，这样一来具有低通滤波特性的信道的冲激响应波形的拖尾将会造成码间干扰，为此可通过增加a的值来减弱这种拖尾效应，从而减少码间干扰，但却是以牺牲信道的带宽利用率为代价的。

　　为了进一步克服码间干扰的影响，通常在接收端取样判决器前加上一个可调的补偿滤波器对信道特性作进一步的补偿，以使实际系统的性能尽量接近最佳的性能，这个补偿过程称为均衡。

　　对基带系统的性能进行补偿可以在频域实现，也可以在时域实现，前者为频域均衡，后者为时域均衡。频域均衡的基本原理时利用可调滤波器的频率特性取补偿基带系统的频率特性，使包括可调滤波波器在内的基带系统的总特性尽量接近最佳系统特性。下面主要讨论时域均衡。

　　所谓时域均衡就是直接利用波形补偿的方法来校正由于基带特性步理想引起的波形畸变，使校正后的波形在取样判决时刻的码间干扰尽可能小，所以时域均衡也称波形均衡。其原理可用图5来说明：

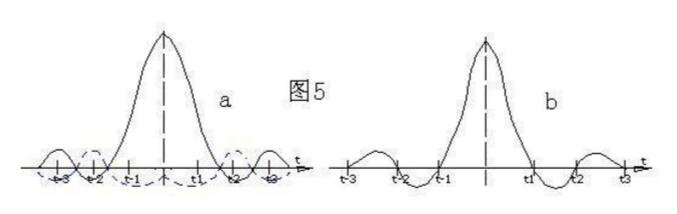
　　图中实线为取样判决器输入端的单个脉冲响应信号，由于信道特性步理性产生了畸变拖尾，在t-3……….t3各取样点上会造成串扰。如果均衡器能产生图中虚线所示的补偿波形，那么经它校正后的波形如图5b所示，在除t0以外所有取样点上的值均为零，从而消除了码间干扰。

　　时域均衡所需要的补偿波形可由接收到的波形经延时加权（加一定的增益）来得到，所以均衡滤波器实际上就是又抽头延时线加上一些可变增益放大器组成得，如图6所示：

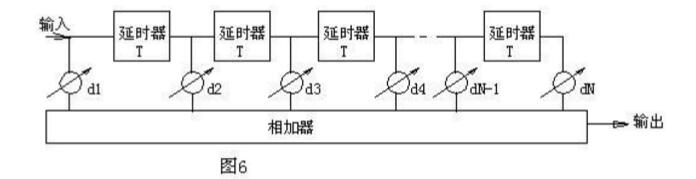
　　它共有N节延时线，每节延时线得延时时间都等于码元得宽度T，在各节延时线之间引出抽头共N＋1个，每个抽头得输出经可变增益（正负可调）放大器d加权后再相加输出。因此当输入有畸变得波形时，只要适当选择可变增益放大器增益就可以使相加器输出得信号对其它码元波形得串扰为最小。

　　均衡滤波器又叫横向滤波器，理论上，均衡滤波器要有无限多个抽头才能作出精确补偿，这当然是步可能的，因为抽头越多，成本也越高，调整也越困难，为了使码间干扰最小，需要找出有限长横向滤波抽头增益d与输出信号之间的关系。

　　另外，上面曾说过，影响误判的还有信道的噪声。那么在调制传输方式信道的噪声、带宽、传输码率式怎么一种关系呢？我看看有名的香农公式：C=Wlog2（1+S/N），从香农公式中我们可以看出：（C是信道容量、W是信道带宽、no是噪声功率密度、N噪声功率、S信号功率。）

　　1、S/N（SNR）↑，C↑。

　　2、如果N→0，SNR→∞，C→∞。无干扰信道的信道容量无穷大。

　　3、W↑，C↑，但趋于一个极限。因为W↑，N=W*n0↑。

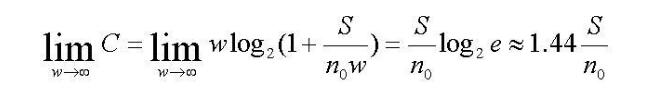
　　4、若C为常数，W与SNR可以互换。（扩频通信）

　　5、信道容量为C，信源的信息速率为R，如果R《C，则可使用信道编码方法实现无误传输。

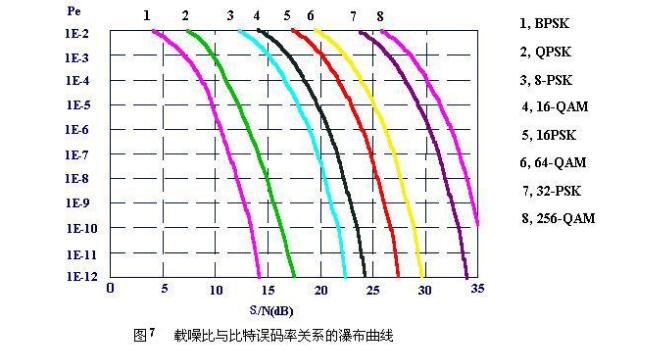
　　从图7上可以看出，对任何一种给定的调制技术，传输信道的信噪比（S/N）越高，则其比特误码率（BER）特性就会越好。换句话说，对任何一种给定的调制技术，如果希望传输信道的比特误码率特性更好，就要提高传输信道的信噪比。

　　当然，以上分析是在理想情况下的结论，实际情况要复杂得多。但不管是噪声、互调、回波还是侵入噪声影响，其结果都是劣化了信道的信噪比，最终都是劣化了信道的无纠错比特误码率BER。

　　从图7看出，曲线在水平轴上的位置取决于调制方式，调制方式抗噪性能越佳，则传输系统在得到相同BER值时所要求的S/N值就越小。一般来说，

　　综上所述，由于数字信号是脉冲矩形波，所以其频谱为无限宽，但是传输信道的带宽是有限的，其特性相当于一个低通滤波器。数字脉冲信号通过一个低通滤波器将会丢失相当一部分的高频频谱，致使信号产生失真，为此，在接收端采用了判决再生的方法重新产生数字脉冲信号。

　　由于数字脉冲信号通过信道时产生失真，使其在时域上的周期变长而产生了码间干扰。这些码间干扰将会使判决产生误判，使重建的数据脉冲产生误码。为了减少码间干扰，可采取使信道具有升余弦滚降特性，使码间干扰控制在判决门限电平之下。我们在接收端也可以通过均衡技术来消除判决点处的码间干扰，使传输信道达到最佳状态，从而实现数字信号的无失真传输。

　　在采用调制方式传输的信道里，在一定的信道带宽和要求的数据速率及要求的误码率下，我们可通过信道调整和选择相应的调制方式来达到数据传输的要求。