了解这些基本分析技术将为为项目的开发和数据的理解带来更多的益处

不管你怎样看待数据科学家的研究工作，都不能轻易忽略对数据进行分析、组织和梳理的重要性。Glassdoor 网站收集了大量的雇主和员工的反馈数据，发现数据科学家位列 "美国最好的 25 个职位"榜首。尽管摘得这一桂冠，但需要数据科学家们研究的工作内容还在不断新增。随着机器学习等技术越来越普遍的应用，深度学习等热门领域受到研究人员和工程师以及企业的关注日渐增加，数据科学家必将继续站在技术创新的浪潮之巅，引领着时代的技术变革。

因此他们需要系统地研究统计机器学习，该学科脱胎于统计学和泛函分析，并结合了信息论、最优化理论和线性代数等多门学科。尽管强大的编程能力对数据科学家而言十分重要，但数据科学家也不完全就是软件工程师。事实上熟练掌握Python对于他们就已足够，真正重要的是同时具备编程、统计和批判思维的能力。

正如Josh Wills所言：“数据科学家比程序员擅长统计学，比统计学家擅长编程。” 很多软件工程师想转型数据科学家，但他们盲目地使用 TensorFlow 或 Apache Spark 等机器学习框架来处理数据，却忽略了背后的统计学理论知识。也就是统计学习理论，机器学习的理论框架，这些都源自统计学和泛函分析。

那么为什么要学习统计学习？我们只有深刻理解了不同技术背后的想法，才能学以致用。也只有先易后难，才能游刃有余、融会贯通。同时，准确评估一种方法的性能也非常重要，不仅能知道工作效果的好坏，也能得知方法的适用范围。此外，统计学习也是一个令人振奋的研究领域，在科学、工业和金融领域都有重要的应用。最后，统计学习是培养现代数据科学家的基础要素。统计学习问题应用的例子如下：

确定前列腺癌的风险因素

根据对数周期图对录音进行分类

根据人口统计学、饮食和临床测量预测是否会患有心脏病

定制垃圾邮件检测系统

识别手写邮政编码

对组织样本进行癌症分类

建立人口调查数据中的薪资与人口统计变量的关系

在介绍常用的10种统计技术之前，我们需要先区分一下机器学习和统计学习，主要有以下几点区别：

机器学习是人工智能的一个分支

统计学习是统计领域的一个分支

机器学习更侧重于大规模应用和预测的精准性

统计学习强调模型及其解释性、精度和不确定性

但区别也在变得越来越模糊，两者很多时候交织在一起

不得不说，市场营销把机器学习炒得很热

线性回归

在统计学中，线性回归是一种通过拟合因变量和自变量之间的最佳线性关系来预测目标变量的方法。最佳拟合即表示由当前的线性表达式得到的预测输出与实际观测值的误差和最小。

线性回归主要分为简单线性回归和多元线性回归。简单线性回归使用一个自变量来拟合最佳线性关系预测因变量；而多元线性回归使用多个自变量来拟合最佳线性关系预测因变量。

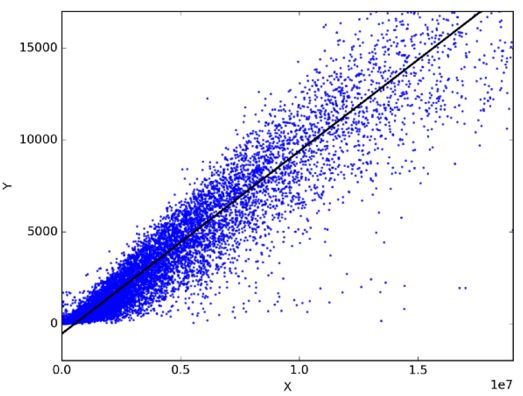
那么线性回归可以用在哪些实际问题上呢？实际上任意选择日常生活中相关的两件事，你便能通过线性回归模型得到他们之间的线性关系。比如你有了过去三年的月消费、月收入和月旅行次数的数据，那你可以预测下一年月支出，还可以知道是月收入还是月旅行次数对月消费更影响，甚至还能用方程式表达月收入、月旅行次数、月消费三者之间的关系呢。

分类

分类是属于一种数据挖掘技术，将数据集分成多个类别可以帮助更准确的预测和分析。分类是一种高效分析大型数据集的方法，典型的代表有逻辑回归(Logistic Regression) 分析和判别分析 (Discriminant Analysis）。

逻辑回归分析适合用于因变量为二元类别时的回归分析。 和所有回归分析一样，逻辑回归也属于预测分析。 Logistic回归用于描述数据，并解释二元因变量与一个或多个名义、序数、区间或比率级别等描述性的自变量之间的关系。 适合逻辑回归的问题类型有：

体重每超出标准体重一磅或每天每抽一包烟对得肺癌概率是否有影响（是或否）。

卡路里摄入、脂肪摄入和年龄对心脏病是否有影响（是或否）。

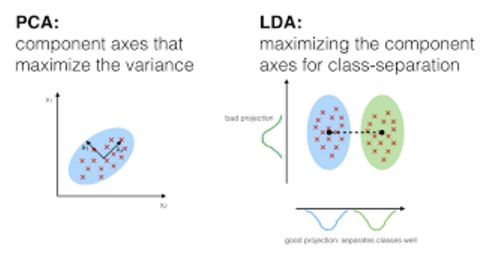
在判别分析中，两个或多个已知的集合、簇或群体都可以作为分类的先验知识，使用时根据被测特征就可把新的观测值划分到相应类别。判别分析会对每个类中的预测因素 X 分别进行建模，然后根据贝叶斯定理便能将其转换成只需根据 X 值就可获得对应类别的概率估计。此类模型既可以是线性判别分析，也可以是二次判别分析。

Linear Discriminant Analysis线性判别分析，通过自变量的线性组合对每个观测值计算“判别分数”，并对其所处的响应变量Y类别进行分类。它假设每个类别内的观测值都服从多变量高斯分布，且每个类别的方差一样。

Quadratic Discriminant Analysis二次判别分析，提供了另一种方法。与LDA一样，QDA也假设来自Y的每类观察值都服从高斯分布。但与LDA不同的是，QDA假定每个类别都有其自己的协方差矩阵，也就是说每个类别的方差不一样。

重采样方法

重采样方法就是从原始数据样本中重复提取样本，属于统计推断的非参数方法。重采样不使用通用分布表来逼近地计算概率 p 的值，而是基于实际数据生成一个独特的采样分布。这种采用分布通过经验性方法生成，而不是分析方法，它能够基于数据所有可能结果的无偏样本获取无偏估计。为了很好的理解重采样的概念，我们需要先了解Bootstrapping和交叉验证（Cross-Validation）：

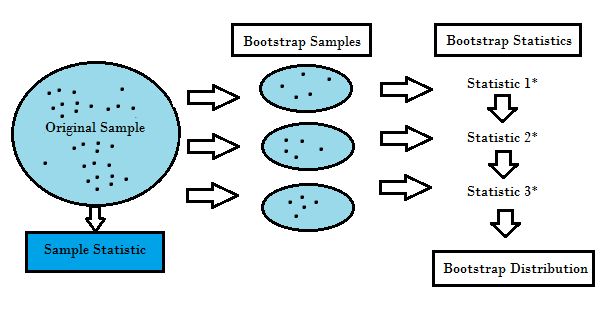
Bootstrapping是有助于在许多情况下验证预测模型的性能和集成方法，估计模型的偏差和方差。 它通过对原始数据进行有放回的采样，并将“未被选择”的数据点作为测试用例。 我们可以多做几次这样的操作，然后用平均值来作为我们对模型性能的估计。

Cross validation交叉验证通过将训练数据分成k个部分来验证模型性能，使用k-1部分作为训练集，余下的部分作为测试集。 重复不同的k次后，将k个分数的平均值作为模型的性能估计。

通常对于线性模型而言，普通的最小二乘法是拟合数据时的主要标准。 接下来的3种方法可以为线性模型拟合提供更好的预测精度和模型可解释性。

子集选择

子集选择的主要目的是挑选出与问题最相关的 p 个预测因子，然后使用该子集特征和最小二乘法拟合模型。

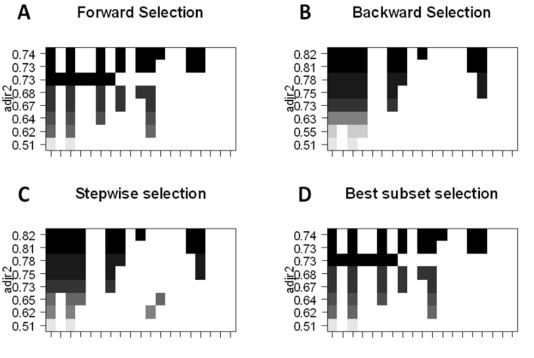
最佳子集的选择，我们可以为 p 个预测因子的每个组合分别拟合普通最小二乘回归，然后再观察各个模型的拟合结果。算法分为两个阶段：（1）拟合包含 k 个预测因子的所有模型，其中 k 表示模型的最大长度；（2）使用交叉验证预测损失选择单个模型。要记住，不能单纯使用训练误差评估模型的拟合情况，验证集或测试集的误差也是十分重要的，因为 RSS 和 R^2 会随变量的增加而单调递增。最好的方法就是通过选择测试集中最高的 R^2 和最低的 RSS 来交叉验证，从而选择模型。

前向逐步选择，可以选出 p 个预测因子的较小子集。算法先从不包含预测因子的模型开始，然后逐步地添加预测因子到模型中，直到所有预测因子都包含在模型中。添加预测因子的顺序是根据不同变量对模型拟合性能提升的程度来确定的，不断添加新的预测因子，直到交叉验证误差没有大的改变。

后向逐步选择，与前向逐步选择相反，首先模型包含所有 p个 预测因子，然后迭代地移除用处最小的预测因子。

混合法，主体遵循前向逐步方法，但在添加每个新变量之后，该方法可能还会移除对模型拟合无用的变量。

特征缩减技术

特征缩减技术使用了所有 p 个预测因子进行建模，然而，表示预测因子重要性的系数将随最小二乘误差向零收缩，这种收缩也称之为正则化，它旨在减少方差以防止模型的过拟合。常用的缩减系数方法有lasso(L1正则化)，岭回归(L2正则化)。

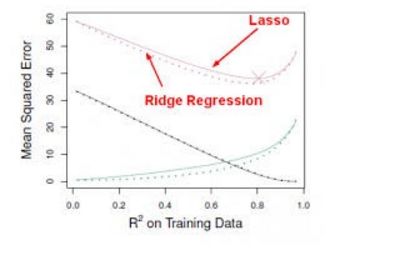
Ridge regression岭回归，跟最小二乘法很像都是寻求减少 RSS 的系数估计，只不过它是通过对损失函数(即优化目标)加入惩罚项，使得训练求解参数过程中会考虑到系数的大小。我们不需要数学分析就能看出 Ridge 回归很擅长于将特征收缩到最小的子空间中。如主成分分析PCA，通过Ridge 回归可以将数据投影到低维空间，并在系数空间内收缩较低方差的成分而保留有较高方差的成分。

但Ridge 回归有一个缺点，最终的模型需要包含所有 p 个预测因子，这源于尽管惩罚项将会令许多预测因子的系数逼近零，但又一定不等于零。虽然这对预测准确度并没有什么影响，却令模型的结果更难以解释。Lasso 方法就很好的克服了这一缺点，因为它能在 s 足够小的时候迫使一些预测因子的系数归零。当 s = 1 时，就像正常的OLS 回归，而当 s 逼近 0 时，系数将收缩到零。因此 Lasso 回归同样是执行变量选择的好方法。

降维（维数减约）

降维是将将p + 1个系数估计问题简化为为M + 1系数估计问题，其中M

Principal Components Regression主成分回归，是从大量的变量中寻找低维特征集的方法。数据中的第一主成分（first principal component）是指观测数据沿着这个变量方向的变化最大，也就是说若用 p 个不同的主成分分别拟合数据，那第一主成分必然是最接近数据分布的那条线。第二主成分是和第一主成分不相关的变量的线性组合，且在该约束下有最大的方差。主要思想是主成分能在各个互相垂直的方向使用数据的线性组合得到最大的方差。基于这种方法，我们还能结合相关变量的效应从数据中获取更多的信息，毕竟在常规的最小二乘法中需要舍弃其中一个相关变量。

由于PCR 方法需要得到 X 的最优线性组合。由于 X 对应的输出 Y 对主成分方向的计算没有影响，也就是说这些组合（方向）是通过无监督方法获得的，那么就无法保证这些方向是预测器的最优表征，也无法保证能获得最优预测输出。偏最小二乘法（PLS）作为 PCR 的代替方法，属于有监督方法。和 PCR 类似，PLS 也是一种降维方法，它首先提取一个新的较小的特征集合（原始特征的线性组合），然后通过最小二乘法将原来的模型拟合为一个新的具有 M 个特征的线性模型，通过对模型预测误差来评价特征集合是否是Y的最优线性组合。

非线性模型

在统计学中，非线性回归属于回归分析的一种形式，通过模型参数的非线性组合来（依赖于一个或多个独立变量）对观测数据建模，并使用逐次逼近法来拟合数据。以下是几种处理非线性模型的重要技术:

阶梯函数（step function），变量为实数，可以写成区间的效用函数的有限线性组合的形式。通俗的讲，阶梯函数就是一种只有有限部分的分段常数函数。

分段函数（piecewise function）通过多个子函数定义，且每一个子函数被定义在确定的区间上。分段实际上是函数的表示方式，而不是函数自身特性，但通过额外的限定条件，它也可以用于描述函数本身。例如，一个分段多项式函数是一个在每一个子定义上为多项式的函数，其中每一个多项式都可能是不同的。

样条曲线（spline）是一种用多项式分段定义的特殊函数。在计算机图形学中，样条曲线是一种分段多项式参数化曲线。由于结构简单、评估简易和精度高，以及通过曲线拟合和交互曲线设计就能逼近复杂曲线的能力，使得样条曲线很常用。

广义加性模型（generalized additive model）是一种广义线性模型，其中线性预测器线性依赖于某些预测器变量的未知平滑函数，其主要作用就是推断这些平滑函数。

基于树的方法

基于树的方法可以用于回归和分类问题，它会将预测器空间分层或分割成一些简单的区域。由于预测器空间的分裂规则集合可以总结为一个树，因此也被称为决策树方法。以下的方法是几种不同的树，它们可以组合起来投票输出统一的预测。

Bagging 能通过从原始数据中生成额外的训练数据（通过组合和重复生成和原始数据大小相同的多段数据）来减少预测的方差，但无法提高模型的预测能力。

Boosting 是一种计算输出的方法，使用多个不同的模型，然后使用加权平均的方法对结果取平均值。一般结合各方法的优势来改变这些方法所占的权重，此外，针对更宽泛的输入数据还可以微调参数得到更佳的预测能力。

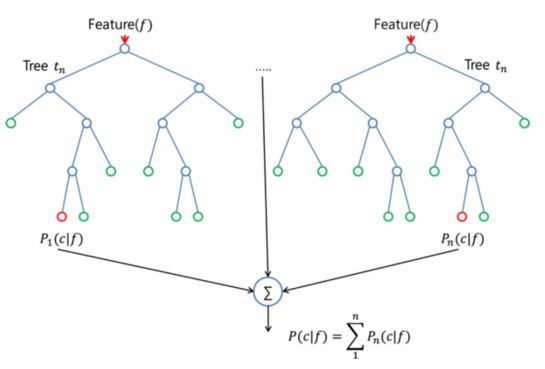
随机森林算法（random forest algorithm）实际上和 bagging 算法很相似，同样是对训练集提取随机 bootstrap 样本。然而，除了 bootstrap 样本以外，还可以提取特征的随机子集来训练单个树；在 bagging 中，则需要为每个树提供全部的特征。由于特征选择是随机的，相比常规的bagging 算法，每个树之间更加独立，从而通常能获得更好的预测性能（得益于更好的方差-偏差权衡）。由于每个树只需要学习特征的一个子集，因此速度也得以提升。

支持向量机

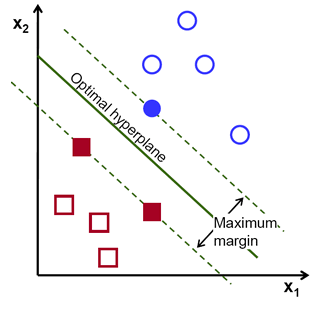
支持向量机（SVM）是一种常用的有监督学习分类技术。通俗地说，它寻找两类点集的最优超平面（hyperplane，在 2D 空间中是线，在 3D 空间中是面，在高维空间中就是超平面。超平面是n 维空间的 n-1 维子空间）。这个超平面使得两类点集的间隔最大，本质上是约束最优化问题，在一定约束下使得间隔最大化，从而实现数据的完美分类。

"支持向量"，就是那些支持着超平面的数据点，也可以说是离超平面最近的数据点。在上图中，蓝色填充圆和两个填充方块就是支持向量。使用过程中，当两类数据线性不可分时，数据点可以通过核函数投影到高维空间中，使得数据变得线性可分。而多分类问题也可以分解成多个"一对一"（one-versus-one）或"一对剩余"（one-versus-rest）的二分类问题。

无监督学习

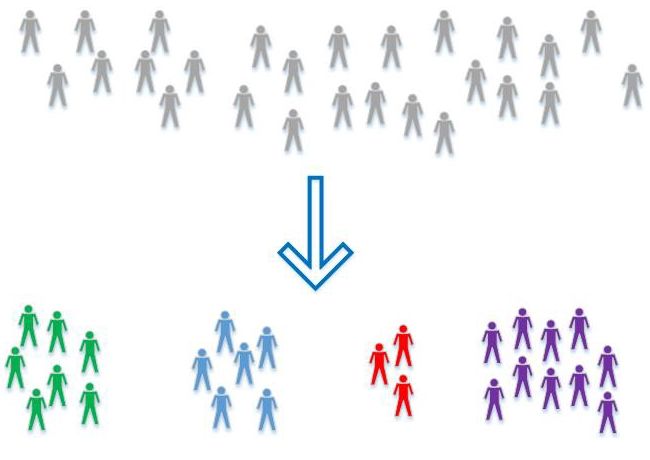
有监督学习是机器学习中的一大部分，其中数据分类已知。当数据分类是未知时，就需要使用另一种技术了，就是无监督学习，它们需要自己去发现数据中的模式。聚类（clustring）是一种典型的无监督学习，数据会根据相关性被分为多簇。以下是几种最常用的无监督学习算法：

Principal Component Analysis 主成分分析：通过保留具备最大方差和互相不相关的特征之间的线性组合，可以生成数据集的低维表示。它还有助于理解无监督学习中的隐变量交互。

k-Means clusteringk 均值聚类：属于硬聚类算法，根据数据到聚类中心的距离将其分成 k 个不同的簇。

Hierarchical clustering层次聚类：由于k-means算法始终有K值选择和初始聚类中心点选择的问题，而这些问题也会影响聚类的效果。为了避免这些问题，我们可以选择另外一种比较实用的聚类算法，就是层次聚类算法。顾名思义，层次聚类就是一层一层的进行聚类，可以自顶向下把大的类别（cluster）分割，叫作分裂法；也可以自下而上对小的类别进行聚合，叫作凝聚法；但是一般用的比较多的是由下向上的凝聚方法。

以上就是一些帮助数据科学家理解数据基本的统计技术，了解这些基本分析技术将为为项目的开发和数据的理解带来更多的益处，对数据的抽象和操作会变得更加容易。希望这篇文章能帮助小伙伴们在理解数据科学的路上带来一些新的收获。