

信号与系统
描述
一. 能量信号和功率信号
有两个重要的概念: 能量信号和功率信号, 能量有限的信号即为能量信号, 其平均功率为零; 功率有限的信号即为能量信号, 其能量为无限大. 关于能量信号和功率信号的计算, 涉及一个很重要的定理, 即帕塞瓦(Parseval)定理, 在考研中经常要考到, 是一个重要的知识点. 简单说, 信号的能量和功率的计算, 既可以在时间域(时域)中进行, 也可以在频率域(频域)中进行, 计算的结果是一样的. 帕塞瓦定理的运用提供了一些出考题的机会, 比如让你计算一个积分, 其物理含义是在时域计算信号的能量, 但是计算很困难, 那么可以用帕塞瓦定理转化为在频域里面计算, 往往比较简单. 但是, 有的考研题目出得并不好, 不用帕塞瓦定理, 直接用高等数学的知识就可以求解.
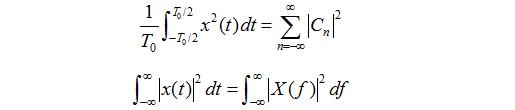
帕塞瓦定理的两种形式
二. 信号的运算
信号的运算基本只涉及数学知识, 即函数的运算, 但是也涉及一些重要的概念, 比如线性和调制等. 线性就是齐次性和可加性, 涉及到信号的相加; 把一个基带信号和一个高频正弦信号相乘, 就是一个调制过程, 实现了频谱的搬移. 还有信号的展缩, 后面会把它和频域的对应关系联系起来: 信号在时域伸展, 那么在频域就压缩, 反之亦然, 频域和时域的展缩性刚好相反. 当一个信号在时域宽度为零时, 那么在频域宽度就是无限的, 比如冲激信号. 信号的运算中的画图是基本功, 数学学得好的中学生应该都能画图.
三. (连续)信号的导数和积分
高等数学里面的函数性质一般是良好的, 可以连续求导和积分, 而本课程中引入的一些信号, 如冲激信号和阶跃信号等, 性质是很不好的, 但是我们仍然可以引入求导和求积的运算, 往往会给一些计算带来方便. 有时, 性质最不好的信号, 却具有最好的性质, 比如冲激信号δ(t)和任何信号做卷积运算, 得到信号本身, 即
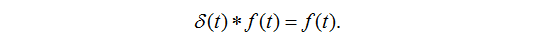
性质最不好的信号δ(t), 在卷积中运算中的地位, 居然和1在普通乘法中的地位一样! 所以, 不要害怕这些所谓性质不好的信号, 它们可能在其他方面的性质是很好的!
信号的求导和积分, 在各种变换中都有对应的性质, 比如用拉氏变换求解微分方程, 涉及信号的导数的拉氏变换.
四. (离散)信号的差分和迭分
这两个运算和连续信号的微分和积分是对应的. 差分分前向差分和后向差分, 大多数教材采用后向差分的形式, 两种差分形式本质上是一样的, 在具体计算上有一点差别, 以后在讲到离散信号与系统的时域分析时, 我们可以从例子看出两个差分的差别. 迭分就是一种求和.
五. 四个重要信号
在连续和离散系统中, 分别介绍了两个重要的基本信号, 我们必须把它们的名称分清: 连续系统中分别是阶跃信号ε(t)和冲激信号δ(t), 离散系统中分别是阶跃序列ε(k)和脉冲序列δ(k), 其中脉冲序列δ(k)在有的数字信号处理教材中称为单位采样序列. 常言说, 名不正则言不顺, 我们要把各种不同的信号很清晰地表达出来, 以免混淆.
-
[3.4.1]--3.3信号与系统的时域和频域特性jf_75936199 2023-05-31
-
[9.14.1]--利用MATLAB分析离散信号与系统jf_90840116 2022-12-11
-
[1.7.1]--信号与系统的应用jf_90840116 2022-12-10
-
#硬声创作季 #信号与系统: 卷积和jf_27932003 2022-12-09
-
#硬声创作季 信号与系统:7-1-1离散时间信号与系统Mr_haohao 2022-10-31
-
#硬声创作季 信号与系统:信号与系统简介(宣传片)Mr_haohao 2022-10-30
-
信号与系统# 卷积jf_43140676 2022-10-21
-
#硬声创作季 信号与系统:217-教学录像-信号系统的严密性Mr_haohao 2022-10-01
-
信号与系统综合实验2016-12-17 741
-
信号与系统实验系统2016-10-11 630
-
信号与系统2016-05-10 725
-
信号与系统试卷及答案2012-07-16 1018
全部0条评论

快来发表一下你的评论吧 !

