怎样才能学好电路分析

　　学好电路分析的思路

　　学好电路分析是后续课程的基础，可谓简单而重要，只有电路分析学好了，在后续课程中才能有良好的思路去解决问题。

　　电路是一门专业基础课，相对于文化基础课来说，它更侧重于解决工程实际问题，而比起专业课来讲，它则更强调物理概念和一般理论分析。

　　电路理论是从实际事物中抽象出来的，与实际事物既有联系又有区别的理论，因此要特别注意应用场合的条件。电路课程具有特殊的规律，掌握了规律则学习起来就轻松多了，也容易记忆。

　　电路理论分析一是主要决定电路元件模型，即理想电阻元件、电感元件、电容元件，掌握了这些元件的伏安特性，则许多问题就迎刃而解。

　　要注意电路结构所遵循的原则即基本尔霍夫二大定律是解决电路结构问题的关键，在以上基础上应用电路中的主要原理、定理，即叠加定理、戴维南定理，对电路进行分析、计算。

　　为了正确、简单的分析、计算电路，对于复杂电路必须通过等效变换进行化简，这是电路理论中的首要手段，所谓等效即在不影响所需计算分析的情况下对外电路等效，这是必须牢牢掌握的。

　　平时要认真阅读例题。例题是课程内容的组成部分，又是从概念到解题的中间桥梁，把定律、定理、原理以例题形式编入书中，这是电路教材的特点。 多做习题也是电路课学习的重要方面。习题是教材中不可分割的重要部分，习题的练习，有助于加深对基本概念的理解。习题不但要做对，更应该理解每道习题所要考察的概念，搞清为什么要出这一道题，考核了什么内容，这样学习才能学得深，学得好。解习题是培养思考能力的一个极其重要的环节，同时也是检验自己是否真正掌握了概念的一把尺子。

　　区别电路模型与实际器件。 理想电路元件是从实际电路器件中科学抽象出来的假想元件。应当注意电路元件与实际器件的联系和差别。一般器件都可以用理想电路元件及它们的组合来模拟，但两者之间不完全等同。例如，在频率不太高的条件下，一个线圈的数学模型就是电阻元件和电感元件的串联，而当频率较高时，线圈的绕线之间的电容效应就不容忽视，在这种情况下表征这个线圈的较精确的模型还应当包含电容元件。

　　区别在不同区域中分析计算的特殊问题。对于电路理论的分析、计算，形式不是一成不变的。比如：在时域中计算时所使用的理想元件伏安特性，以及结构特征所表示的方法，在频域中就不适用。这就给我们一个启示，任何一种在一定范围内计算、分析所使用的元件伏安特性、结构定律、原理、公式，换到另一范围使用时，必须考虑在新范围内使用时所发生的特殊问题，修正以前的表达式，而且，经过处理后解决了这些问题，则以前所学的方法都可在新范围内使用。电路分析就是不断地寻找各种方法来解决问题，因此特别注意在新范围内使用所必须的条件。 总之，要想学好电路理论，必须多想、多算、多动手。

　　

　　最实用的电路分析方法盘点

　　一、方框图识图方法

　　图1-2所示是一个两级音频信号放大系统的方框图。从图中可以看出，这一系统电路主要由信号源电路、第一级放大器、第二级放大器和负载电路构成。从这一方框图也可以知道，这是一个两级放大器电路。

　　

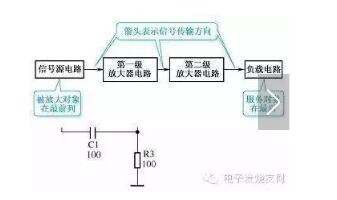
　　图1-2方框图示意图

　　二、单元电路图识图方法

　　单元电路是指某一级控制器电路，或某一级放大器电路，或某一个振荡器电路、变频器电路等，它是能够完成某一电路功能的最小电路单位。从广义上讲，一个集成电路的应用电路也是一个单元电路。

　　学习整机电子电路工作原理过程中，单元电路图是首先遇到的具有完整功能的电路图，这一电路图概念的提出，完全是为了方便电路工作原理分析之需要。

　　1.单元电路图功能

　　单元电路图具有下列一些功能。

　　（1）单元电路图主要用来讲述电路的工作原理。

　　（2）单元电路图能够完整地表达某一级电路的结构和工作原理，有时还会全部标出电路中各元器件的参数，如标称阻值、标称容量和三极管型号等。如图1-18所示，图中标出了可变电阻器和电阻器的阻值。

　　

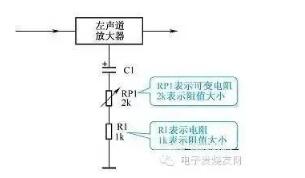
　　图1-8示意图

　　（3）单元电路图对深入理解电路的工作原理和记忆电路的结构、组成很有帮助。

　　2.单元电路图特点

　　单元电路图主要是为了分析某个单元电路工作原理的方便，而单独将这部分电路画出的电路图，所以在图中已省去了与该单元电路无关的其他元器件和有关的连线、符号，这样，单元电路图就显得比较简洁、清楚，识图时没有其他电路的干扰，这是单元电路的一个重要特点。单元电路图中对电源、输入端和输出端已经进行了简化。图1-9所示是一个单元电路。

　　

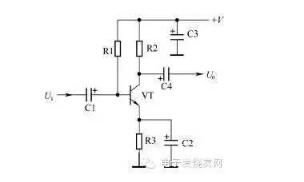
　　图1-9单元电路图示意图

　　（1）电源表示方法。电路图中，用+V表示直流工作电压，其中正号表示采用正极性直流电压给电路供电，地端接电源的负极;用-V表示直流工作电压，其中负号表示采用负极性直流电压给电路供电，地端接电源的正极。

　　（2）输入和输出信号表示方法。Ui表示输入信号，是这一单元电路所要放大或处理的信号;Uo表示输出信号，是经过这一单元电路放大或处理后的信号。

　　三、支路节点法

　　节点就是电路中几条支路的汇合点。所谓支路节点法就是将各节点编号（约定；电源正极为第1节点，从电源正极到负极，按先后次序经过的节点分别为1、2、3……），从第1节点开始的支路，向电源负极画。可能有多条支路（规定：不同支路不能重复通过同一电阻）能达到电源负极，画的原则是先画节点数少的支路，再画节点数多的支路。然后照此原则，画出第2节点开始的支路。余次类推，最后将剩余的电阻按其两端的位置补画出来。

　　例5．画出图10所示的等效电路。

　　

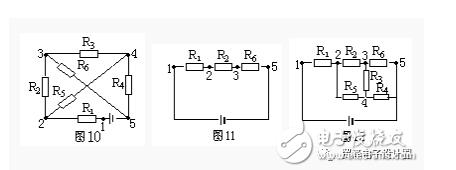
　　解：图10中有1、2、3、4、5五个节点，按照支路节点法原则，从电源正极（第1节点）出来，节点数少的支路有两条：R1、R2、R5支路和R1、R5、R4支路。取其中一条R1R2、R5支路，画出如图11。

　　再由第2节点开始，有两条支路可达负极，一条是R5、R4，节点数是3，另一条是R5、R3、R5，节点数是4，且已有R6重复不可取。所以应再画出R5、R4支路，最后把剩余电阻R3画出，如图12所示。

　　四、几何变形法

　　几何变形法就是根据电路中的导线可以任意伸长、缩短、旋转或平移等特点，将给定的电路进行几何变形，进一步确定电路元件的连接关系，画出等效电路图。

　　例6．画出图13的等效电路。

　　

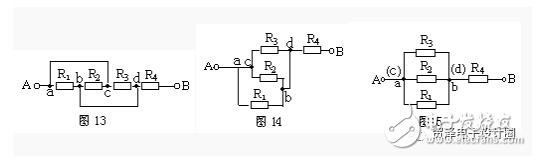
　　解：使ac支路的导线缩短，电路进行几何变形可得图14，再使ac缩为一点，bd也缩为一点，明显地看出R1、R2和R5三者为并联，再与R4串联（图15）。

　　五、撤去电阻法

　　根据串并联电路特点知，在串联电路中，撤去任何一个电阻，其它电阻无电流通过，则这些电阻是串联连接；在并联电路中，撤去任何一个电阻，其它电阻仍有电流通过，则这些电阻是并联连接。

　　

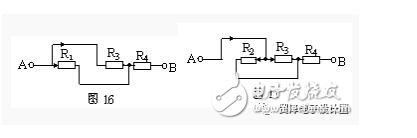
　　仍以图13为例，设电流由A端流入，B端流出，先撤去R2，由图16可知R1、R3有电流通过。再撤去电阻R1，由图17可知R2、R3仍有电流通过。同理撤去电阻R3时，R1、R2也有电流通过由并联电路的特点可知，R1、R2和R3并联，再与R4串联。