理解 RMS 电压

“ 什么是 Vrms ？ 如何推导正弦波的 RMS 值？  ”

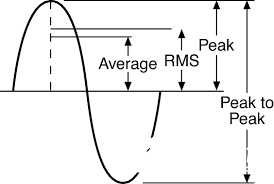
熟悉我的读者都知道，在电子技术类文章中，我始终避免预设读者具备微积分基础。我始终认为，即使在极客群体中，真正精通微积分的人也是凤毛麟角。许多大学的微积分课程充斥着填鸭式教学——那些解释不清的公式需要耗费大量时间死记硬背，却只需转瞬就能忘得干干净净。虽然某些推导确实无法绕开数学工具，但在绝大多数情况下，电气工程类文章对微积分的依赖根本毫无必要。

今天，我要针对当前谷歌搜索排名第一的均方根电压（Vrms）公式推导方法提出尖锐批评。这个推导过程充斥着以下问题：

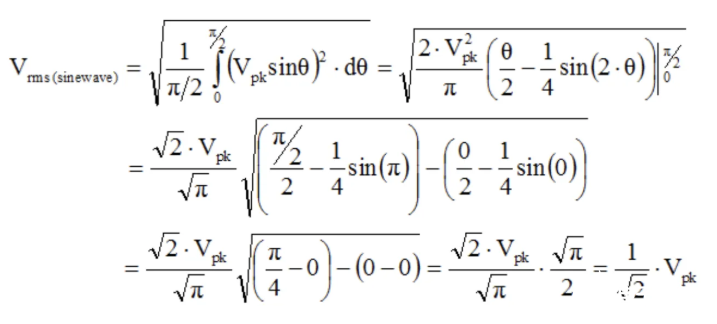  到底什么是 Vrms? 在电路设计中，常需计算已知电阻上随时间变化的电压信号所消耗的功率。例如，设计驱动音响的功放电路时，需确保功率不超过扬声器线圈的额定值（以瓦特为单位）。现代功放多以电压信号驱动，而扬声器阻抗固定，因此需建立电压与功率的等效关系。

计算功率的公式为：

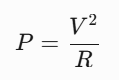
如果电压是恒定的，这个公式没有问题，但如果信号随时间变化呢？

为了回答该问题，我们以一个10Ω负载和分三个离散阶跃变化（1V、10V，再回到1V）的电源电压构成的简化示例进行分析。在这种设置中，每个时间段本质上都是独立的‘稳态’情景，因此可以相应地拆分计算步骤：

这样，我们就可以计算出一个简单的算术平均值，从而得到负载在一段时间内的平均耗散功率：

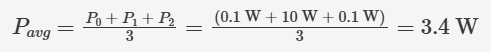
该结果虽然正确，但这种计算方式并不总是便捷。例如，当涉及超过三个电压等级时，针对不同音量旋钮位置重新计算总和将十分繁琐。若我们能找到一个等效直流电压，使其在负载上消耗的功率与待研究的交流信号相同，便能以更直接的方式建模音量与功率的关系。

然而如何计算该等效电压？是否仅对各时间段电压取算术平均值？让我们深入探究：

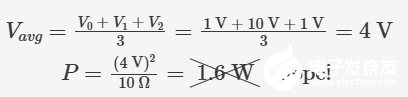  结果并不一致。问题出在功率方程中的 V² 项。为了找出正确的方法，我们可以用符号来求解示例中的功率方程。

组成方程为 P0 = V0 / R、P1 = V1 / R 和 P3 = V3 / R，因此：

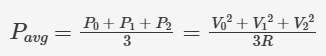
换一种描述方式：

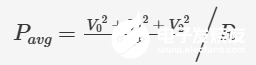
该表达式的前半部分正是电压平方的算术平均值，恰好占据原恒压公式中 V² 的位置！换言之，我们先将原始波形进行平方运算，然后计算其标准算术平均值。
 

无论如何，我们暂且将这个特殊平均值称为x，并验证其数学合理性：

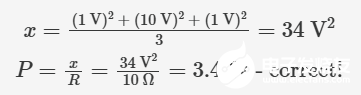
但从物理意义上说，x 究竟代表什么？它并不能代替原始功率表达式中的电压；请记住，它取代的是电压的平方 (V²)。要得到我们说过的功率等效电压，我们需要计算这个值的平方根。

而这正是‘均方根电压’（Vrms）的定义：它是波形平方（S）的算术平均值（M）的平方根（R）。本例中，Vrms = √34 ≈ 5.831 V。我们只需将 Vrms 除以二，即可模拟输入信号振幅减半对耗散功率的影响。

方波在两个电压（Vlo 和 Vhi）之间交替变化的情况与本节前面讨论的方法类似，只是我们只需要计算两个点的平均值，而不是三个点的平均值：

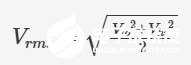
但对于连续变化的信号该如何处理？

正弦函数的 Vrms

在模拟电子领域，我们常需处理正弦信号--此时维基百科通常会引入微积分进行推导。但我们能否避开复杂的积分运算？

答案是可以！回顾可知，计算任意波形的均方根值（RMS），需对波形进行平方（S）、取算术平均（M）、再开平方根（R）三步操作。

我们可以先将波形平方。给定峰值振幅 Vp 的正弦波信号的一般方程如下：

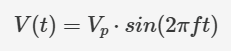
将右侧平方后得到：

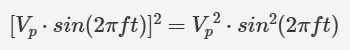
表达式中唯一随时间变化的部分是 sin²(...) 函数。让我们使用一个新符号 Sm 来表示其平均值。这样，我们就可以用下面的方式写出 Vrms 表达式：

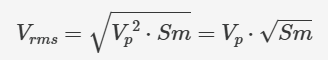
现在，我们要做的就是找出 Sm。要找到任何周期性波形的平均值，我们只需考虑一个周期；任何重复序列的平均值都与单个周期的平均值相同：

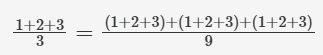
在计算sin²(...)的周期时，必须与平方前的正弦函数周期对齐，即参数范围应限定在0°至360°之间。但即便如此，我们仍需对无限个连续变化的值进行平均运算！

幸运的是，三角函数提供了解决方案。让我们抛开具体的 Vrms 情景，考虑一个由常规三角函数描述的临时构建的直角三角形：

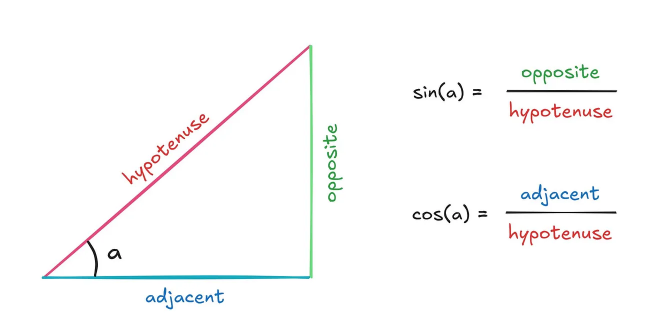
假设我们知道斜边的长度--称之为 n--并知道角度 a。很明显，垂直边的高等于 sin(a) ×n，水平边的长度等于 cos(a) ×n。

这是一个直角三角形，我们还可以用勾股定理来描述它的边之间的关系：斜边的平方等于对边的平方加邻边的平方。

我们已经知道了这些边的值，斜边是 n，其他边由角度 a 的三角函数给出：

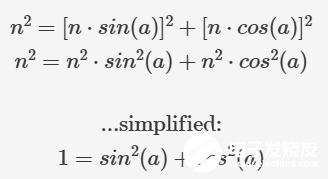
这一普适性法则揭示了正弦平方与余弦平方之间的奇妙关系，被称为毕达哥拉斯恒等式。

现在，让我们回到 RMS 的难题上。为了解释下一步，想象一下你只在储蓄罐里放 5 美元的钞票，那么储蓄罐里钞票的平均值必然是 5 美元。同样，如果存在这样一个约束条件，即对于每个给定的 a，sin²(a) + cos ²(a)之和等于 1，那么在任何常见角度范围内，sin²(...)和 cos²(...) 的平均值之和必然具有相同的性质。我们之前引入了 Sm 来表示 sin²(...) 的算术平均数；采用 Cm 来表示 cos²(...)，我们可以得到：

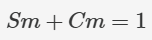
在从 0° 到 360° 的跨度内，正弦函数和余弦函数都完成了一个周期；它们产生了两个完全相同的波形，只是在时间上有所偏移。每当 sin(...) = 0.5 时，就会有一个 cos(...) = 0.5 的对应点：

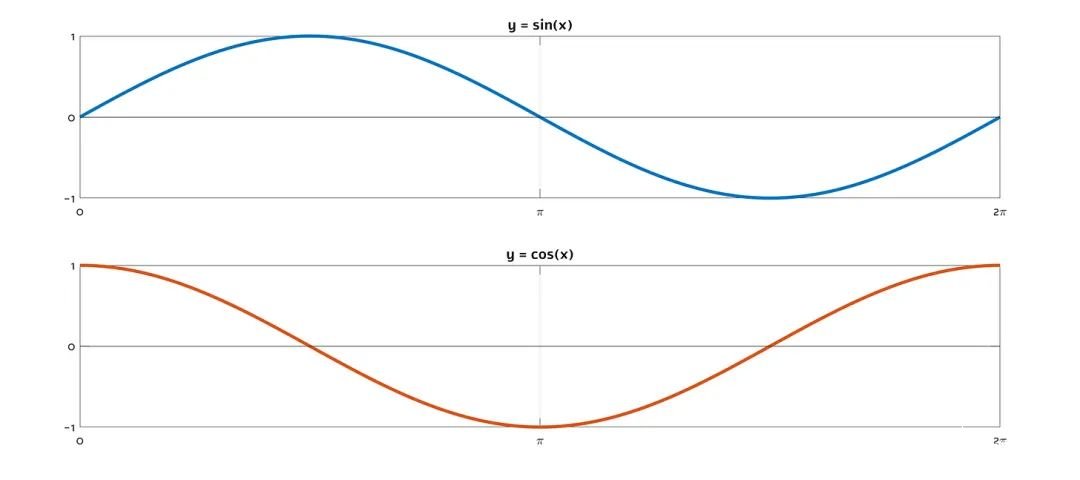
事实上，我们可以通过对余弦部分进行一些处理来说明这一点：

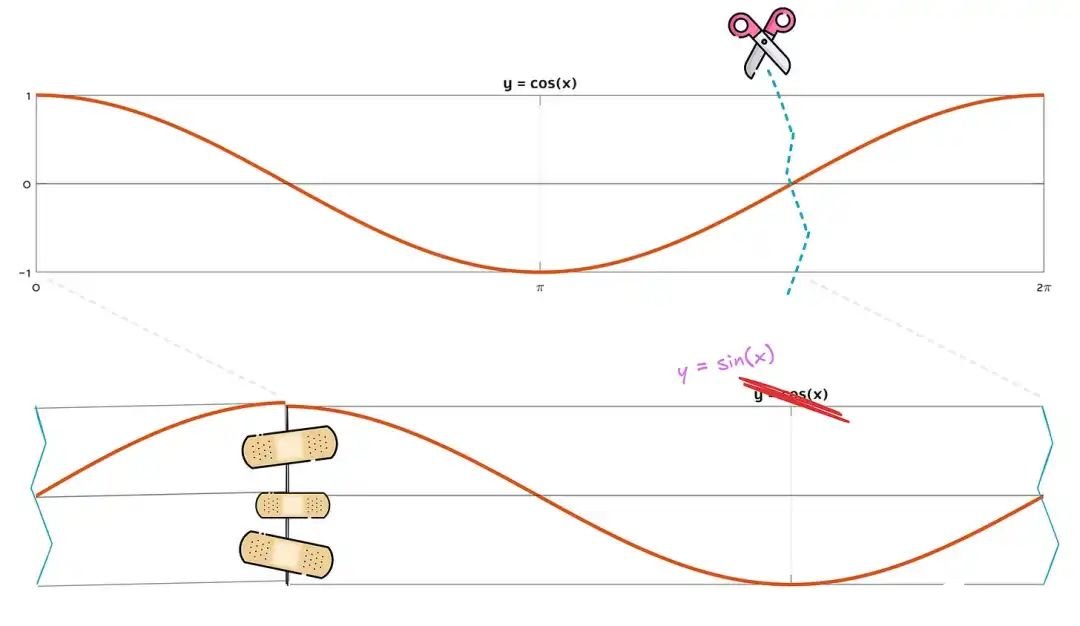
由于波形基本相同，sin(α) 的全周期平均值等于 cos(a) 的全周期平均值。将 sin(a) 和 cos(a) 的每个值平方并不会改变这种关系：我们最终会得到新的曲线，但它们仍然是一条直线，而且每条曲线上的任意两点之间仍然存在 1:1 的对应关系。sin²(a) 的周期-均值一定与 cos²(a) 的周期-均值相同。根据这一观察结果，我们终于可以算出 Sm 的值：

换句话说，我们已经确定 sin²(...) 波形在 0° 和 360° 之间的平均值为 ½。将其插入先前的 Vrms 公式，我们就得到了峰值振幅为 Vp 的 0 V 中心正弦波的通用公式：

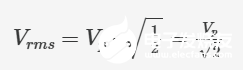
证明完毕，搞定！（小编注：其实还不如用微积分来得方便...）

本文转载自（经过编译及校对）： https://lcamtuf.substack.com/p/whats-root-mean-square-voltage

注意：如果想第一时间收到 KiCad 内容推送，请点击下方的名片，按关注，再设为星标。

常用合集汇总：

和 Dr Peter 一起学 KiCad

KiCad 8 探秘合集

KiCad 使用经验分享

KiCad 设计项目（Made with KiCad）

常见问题与解决方法

KiCad 开发笔记

插件应用

发布记录

审核编辑 黄宇