怎样区分线性和非线性_线性与非线性的区别（线性分析、线性模型）

　　怎样区分线性和非线性

　　1、线性linear，指量与量之间按比例、成直线的关系，在数学上可以理解为一阶导数为常数的函数；

　　非线性non-linear则指不按比例、不成直线的关系，一阶导数不为常数。

　　2、线性的可以认为是1次曲线，比如y=ax+b ，即成一条直线

　　非线性的可以认为是2次以上的曲线，比如y=ax^2+bx+c，（x^2是x的2次方），即不为直线的即可。

　　3、两个变量之间的关系是一次函数关系的——图象是直线，这样的两个变量之间的关系就是“线性关系”；

　　如果不是一次函数关系的——图象不是直线，就是“非线性关系。

　　4、“线性”与“非线性”，常用于区别函数y = f （x）对自变量x的依赖关系。线性函数即一次函数，其图像为一条直线。其它函数则为非线性函数，其图像不是直线。

　　线性，指量与量之间按比例、成直线的关系，在空间和时间上代表规则和光滑的运动；而非线性则指不按比例、不成直线的关系，代表不规则的运动和突变。

　　比如，普通的电阻是线性元件，电阻R两端的电压U，与流过的电流I，呈线性关系，即R=U/I，R是一个定数。二极管的正向特性，就是一个典型的非线性关系，二极管两端的电压u，与流过的电流i不是一个固定的比值，即二极管的正向电阻值，是随不同的工作点（u、i）而不同的。

　　5、在数学上，线性关系是指自变量x与因变量yo之间可以表示成y=ax+b ，（a，b为常数），即说x与y之间成线性关系。

　　不能表示成y=ax+b ，（a，b为常数），即非线性关系，非线性关系可以是二次，三次等函数关系，也可能是没有关系。

　　

　　线性模型和非线性模型的区别

　　误区

　　1、线性和非线性的区别是是否可以用直线将样本划分开（这个观点是对的）

　　2、和同学讨论到logistics模型是线性还是非线性的，很难理解！（logistics模型是广义线性模型）

　　3、区分一下回归和分类问题，线性模型是可以用来曲线拟合（回归）的，但是线性模型模型的分类一定是一条直线的，例如logistics模型。

　　线性模型和非线性模型区别

　　1、线性模型可以是用曲线拟合样本，但是分类的决策边界一定是直线的，例如logistics模型

　　2、区分是否为线性模型，主要是看一个乘法式子中自变量x前的系数w，如果w只影响一个x，那么此模型为线性模型。或者判断决策边界是否是线性的

　　3、举例

　　

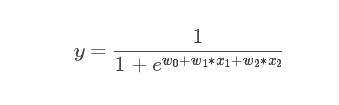
　　画出y和x是曲线关系，但是它是线性模型，因为x1*w1中可以观察到x1只被一个w1影响

　　

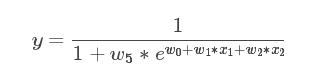
　　此模型是非线性模型，观察到x1不仅仅被参数w1影响，还被w5影响，如果自变量x被两个以上的参数影响，那么此模型是非线性的！

　　4、其实最简单判别一个模型是否为线性的，只需要判别决策边界是否是直线，也就是是否能用一条直线来划分

　　神经网络是非线性

　　虽然神经网络的每个节点是一个logistics模型，但是组合起来就是一个非线性模型。

　　此处我们仅仅考虑三层神经网络

　　

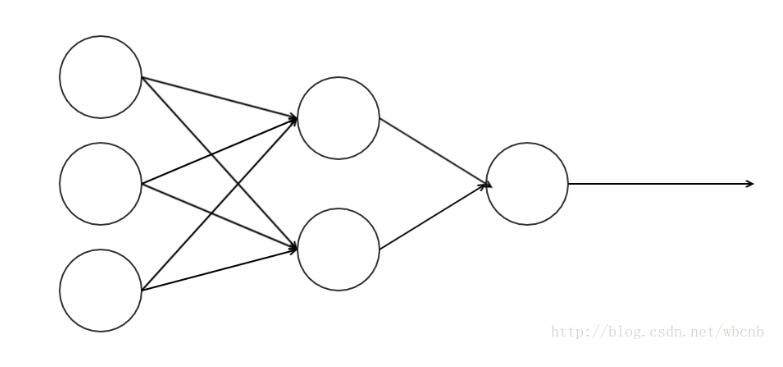
　　第一层的表达式

　　

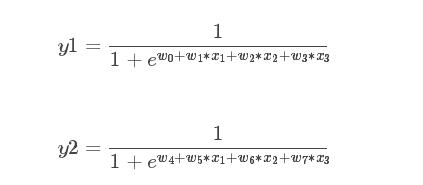
　　第二层的表达式

　　

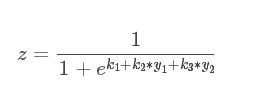
　　将第一层的表达式带入第二层表达式中，可以观察到x1变量不仅仅被w1影响还被k2影响，所以此模型不是一个线性模型，是个非线性模型。

　　线性分析与非线性分析的区别

　　线性分析在结构方面就是指应力应变曲线刚开始的弹性部分，也就是没有达到应力屈服点的结构分析。非线性分析包括状态非线性，几何非线性，以及材料非线性，状态非线性比如就是钓鱼竿，几何比如就是物体的大变形，材料比如就是塑性材料属性。

　　

　　

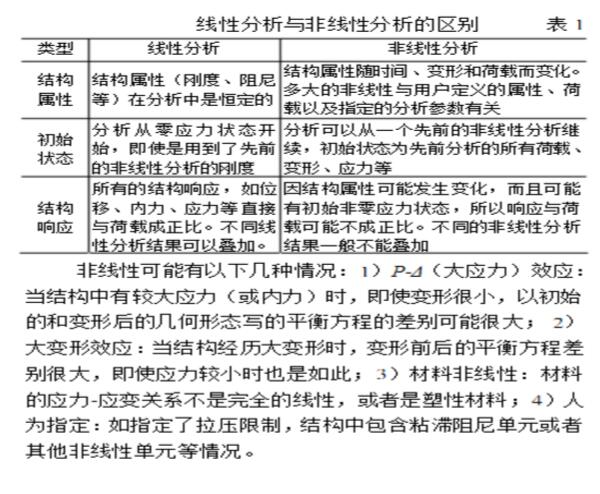
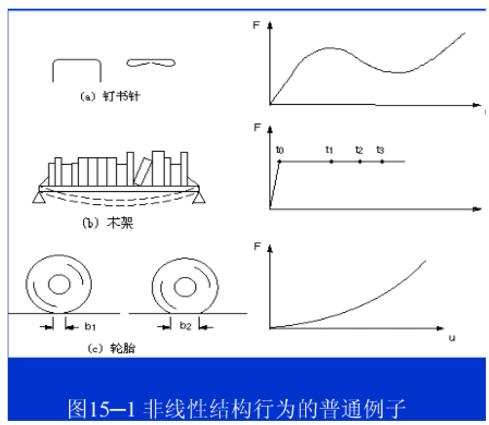
　　2、非线性行为的原因

　　引起结构非线性的原因很多，主要可分为以下3种类型。

　　（1）状态变化（包括接触）

　　许多普通结构表现出一种与状态相关的非线性行为。例如，一根只能拉伸的电缆可能是松弛的，也可能是绷紧的；轴承套可能是接触的，也可能是不接触的；冻土可能是冻结的，也可能是融化的。这些系统的刚度由于系统状态的改变而突然变化。状态改变或许和载荷直接有关（如在电缆情况中），也可能是由某种外部原因引起的（如在冻土中的紊乱热力学条件）。接触是一种很普遍的非线性行为，接触是状态变化非线性类型中一个特殊而重要的子集。

　　（2）几何非线性

　　结构如果经受大变形，其变化的几何形状可能会引起结构的非线性响应。如图5.2所示的钓鱼杆，在轻微的载荷作用下，会产生很大的变形。随着垂向载荷的增加，杆不断弯曲导致动力臂明显减少，致使杆在较高载荷下刚度不断增加。

　　

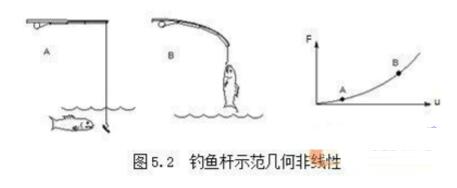
　　（3）材料非线性

　　非线性的应力-应变关系是结构非线性的常见原因。许多因素可以影响材料的应力-应变性质，包括加载历史（如在弹-塑性响应状况下）、环境状况（如温度）、加载的时间总量（如在蠕变响应状况下）等。

　　3、非线性结构分析中应注意的问题

　　（1）牛顿-拉普森方法

　　ANSYS程序的方程求解器可以通过计算一系列的联立线性方程来预测工程系统的响应。然而，非线性结构的行为不能直接用这样一系列的线性方程来表示，需要一系列的带校正的线性近似来求解非线性问题。

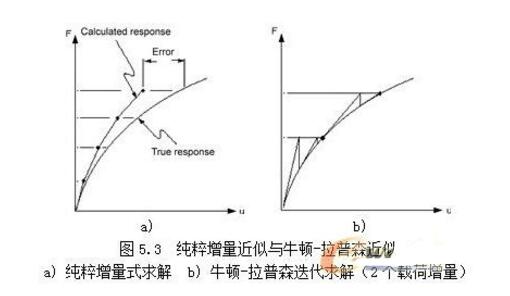
　　一种近似的非线性求解是将载荷分成一系列的载荷增量。可以在几个载荷步内或者在一个载荷步的几个子步内施加载荷增量。在每一个增量的求解完成后，继续进行下一个载荷增量之前，程序调整刚度矩阵以反映结构刚度的非线性变化。遗憾的是，纯粹的增量近似不可避免地随着每一个载荷增量积累误差，最终导种结果失去平衡，如图5.3a所示。

　　ANSYS程序通过使用牛顿-拉普森平衡迭代克服了这种困难，在某个容限范围内，它使每一个载荷增量的末端解都达到平衡收敛。图5.3b描述了在单自由度非线性分析中牛顿-拉普森平衡迭代的使用。在每次求解前，NR方法估算出残差矢量，这个矢量是回复力（对应于单元应力的载荷）和所加载荷的差值。之后，程序使用非平衡载荷进行线性求解，并且核查收敛性。如果不满足收敛准则，则重新估算非平衡载荷，修改刚度矩阵，获得新解，持续这种迭代过程直到问题收敛。