基于Numpy实现神经网络：反向传播

和DeepMind数据科学家、Udacity深度学习导师Andrew Trask一起，基于Numpy手写神经网络，更深刻地理解反向传播这一概念。

总结：基于可以尝试和修改的玩具代码，我能取得最好的学习效果。本教程基于一个非常简单的玩具样例（简短的Python代码实现）介绍反向传播这一概念。

如果你对我的文章感兴趣，欢迎在推特上关注 电子说，也欢迎给我反馈。

直接给我代码

1. X = np.array([ [0,0,1],[0,1,1],[1,0,1],[1,1,1] ])

2. y = np.array([[0,1,1,0]]).T

3. syn0 =2*np.random.random((3,4)) -1

4. syn1 =2*np.random.random((4,1)) -1

5. forjinxrange(60000):

6.    l1 =1/(1+np.exp(-(np.dot(X,syn0))))

7.    l2 =1/(1+np.exp(-(np.dot(l1,syn1))))

8.    l2_delta = (y - l2)*(l2*(1-l2))

9.    l1_delta = l2_delta.dot(syn1.T) * (l1 * (1-l1))

10.    syn1 += l1.T.dot(l2_delta)

11.    syn0 += X.T.dot(l1_delta)

其他语言： D、C++、CUDA

不过，上面的代码有点过于凝练了……让我们循序渐进。

一、微型玩具网络

基于反向传播的神经网络尝试通过输入来预测输出。

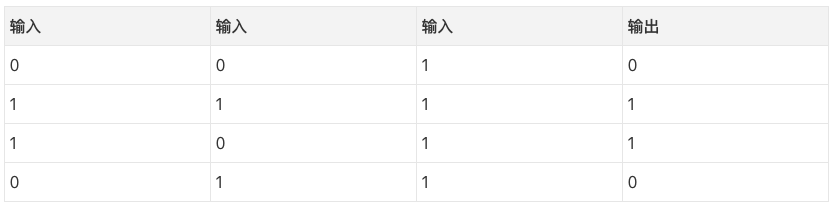
尝试通过上表的输入预测输出。我们可以通过测量输入值和输出值的统计数据来解决这一问题。如果我们这么干，我们会发现最左边的输入和输出完全相关（perfectly correlated）。最简单形式的反向传播，就是通过类似的测量统计数据的方式来建立模型。

双层神经网络

1. importnumpyasnp

3. # sigmoid函数

4. defnonlin(x,deriv=False):

5.    if(deriv==True):

6.        returnx*(1-x)

7.    return1/(1+np.exp(-x))

9. # 输入数据集

10. X = np.array([  [0,0,1],

11.                [0,1,1],

12.                [1,0,1],

13.                [1,1,1] ])

15. # 输出数据集            

16. y = np.array([[0,0,1,1]]).T

18. # 设置随机数种子使计算结果是确定的

19. # （实践中这是一个很好的做法）

20. np.random.seed(1)

22. # 随机初始化权重（均值0）

23. syn0 =2*np.random.random((3,1)) -1

25. foriterinxrange(10000):

27.    # 前向传播

28.    l0 = X

29.    l1 = nonlin(np.dot(l0,syn0))

31.    # 差多少？

32.    l1_error = y - l1

34.    # 误差乘以sigmoid在l1处的斜率

35.    l1_delta = l1_error * nonlin(l1,True)

37.    # 更新权重

38.    syn0 += np.dot(l0.T,l1_delta)

40. print"训练后输出："

41. printl1

1. 训练后输出：

2. [[0.00966449]

3. [0.00786506]

4. [0.99358898]

5. [0.99211957]]

如你所见，“训练后输出："下面打印出的结果说明这一网络是有效的！！！在我描述这个过程之前，我建议你尝试探索以上代码以获得一些它如何工作的感性认识。以上代码应该可以在Jupyter Notebook中直接运行（或者你也可以以脚本的形式运行，但我强烈建议使用notebook）。下面是探索代码的一些提示：

• 比较第一次迭代和最后一次迭代后的l1

• 查看nonlin函数定义。该函数给出一个概率作为输出。

• 查看迭代过程中l1_error的值是如何改变的。

• 仔细看看第36行。这段代码的奥秘主要藏在此处。

• 查看第39行。网络中的一切是为这个操作准备的。

让我们逐行讨论代码。

建议：在两块屏幕上打开本文，这样你就可以一边查看代码，一边阅读文章了。我写作下文的时候基本上就是这么做的。

01行： 导入numpy。numpy是一个线性代数库。这是我们唯一的依赖。

04行： 这是我们的“非线性”。非线性可以有多种选择，这里我们选用的是sigmoid. sigmoid函数将任何值映射到0到1之间的值。我们使用sigmoid将数字转换为概率。sigmoid函数还有其他一些有利于训练神经网络的性质。

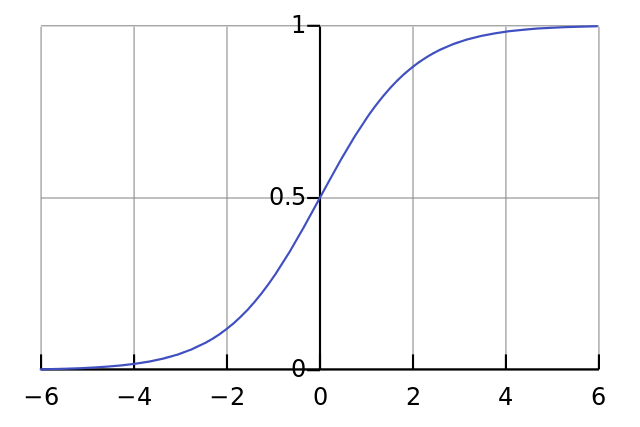
05行： 注意这个函数同时可以生成sigmoid的导数（当deriv=True时）。sigmoid函数有一个非常棒的特性是它的输出可以用来创建它的导数。如果sigmoid的输出是变量out的话，它的导数是out * (1 - out)，非常高效。

如果你不熟悉导数，只需把它想象成sigmoid函数在给定的点上的斜率（如上图所示，不同点的斜率不同）。想要了解更多关于导数的知识，可以参考Khan Academy的导数教程。

10行： 初始化输入数据集为numpy矩阵。每行是一个“训练样本”。每列对应一个输入节点。因此，我们有3个输入节点和4个训练样本。

16行： 初始化输出数据集。这里，我水平地生成了数据集（1行4列），以节省字符。.T是转置函数。转置之后，y矩阵有4行1列。和输入一样，每行是一个训练样本，每列（仅有一列）是一个输出节点。所以，我们的网络有3个输入和1个输出。

20行： 设置随机数种子是一个很好的做法。数字仍然是随机分布的，但它们在每次训练中将以完全一致的方式随机分布。这更便于观察你的改动对网络的影响。

23行： 这是神经网络的权重矩阵。它命名为syn0，意味着它是“突触（synapse）零”。由于我们的网络只有两层（输入和输出），我们只需要一个权重矩阵就可以连接两者。它的维度是(3, 1)，因为我们有3个输入和1个输出。另一种看待它的方式是l0的尺寸是3，l1的尺寸是1. 我们需要将l0中的每个节点连接到l1中的每个节点，因而我们需要一个维度(3, 1)的矩阵。

同时注意，随机初始化时的均值为零。权重初始化有不少理论。就目前而言，可以简单地把这一做法（权重初始化均值为零）看成是最佳实践。

另外需要注意的是，“神经网络”实际上就是这个矩阵。我们有神经网络层l0和l1，但它们其实是基于数据集创建的短暂值。我们并不保存它们。所有的学习所得都储存在syn0矩阵中。

25行： 网络训练代码从这里开始。这是一个“迭代”训练代码的for循环，优化网络以拟合数据集。

28行： 第一层网络l1直接就是数据。因此我们在这里明确声明这一点。还记得X包含4个训练样本（行）吗？在这一实现中，我们将同时处理所有样本。这被称为“全batch”（full batch）训练。因此，我们有4个不同的l0行，但是如有必要，我们可以将它看成一个单独的训练样本。在这里这些没有区别。（如果需要，我们可以加载1000甚至10000行数据，而不用修改任何代码）。

29行： 这是我们的预测步骤。基本上，我们首先让网络“尝试”基于输入预测输出。我们接着研究它的表现，从而加以调整，让它在下一个迭代中表现更好。

这一行包含两小步。首先矩阵l0和syn0相乘。接着将输出传给sigmoid函数。算下维度：

1. (4x3) dot (3x1) = (4x1)

矩阵乘法是有序的，满足等式两边的维度必须一致。因此最终生成的矩阵的行数等于第一个矩阵的行数，列数等于第二个矩阵的列数。

由于我们载入了4个训练样本，我们最终对正确答案做了4次猜测，一个(4 x 1)矩阵。每个输出对应与网络对给定输入的猜测。也许读到这里你能很直观地理解为什么我们之前说如有必要可以载入任意数目的训练样本，因为矩阵乘法仍然可以工作。

32行： 好了，l1根据每个输入作出了“猜测”。我们可以通过从猜测（l1）中减去真实答案（y）来看看它的表现如何。l1_error只是一个由正数和负数组成的向量，反映了网络离正确还差多少。

36行： 现在是关键时刻！这是整个模型的奥秘所在！这一行里发生了很多事情，所以让我们进一步把它分成两部分。

第一部分：导数

1. nonlin(l1,True)

如果l1表示下图中的三点，那么上面的代码生成了下图曲线的斜率。注意，像x=2.0这样很高的值（绿点）和像x=-1.0这样很低的值（紫点）具有相对平缓的斜率。x=0（蓝点）处的斜率最高。这起到了非常重要的作用。同时注意所有的导数都在0和1之间。

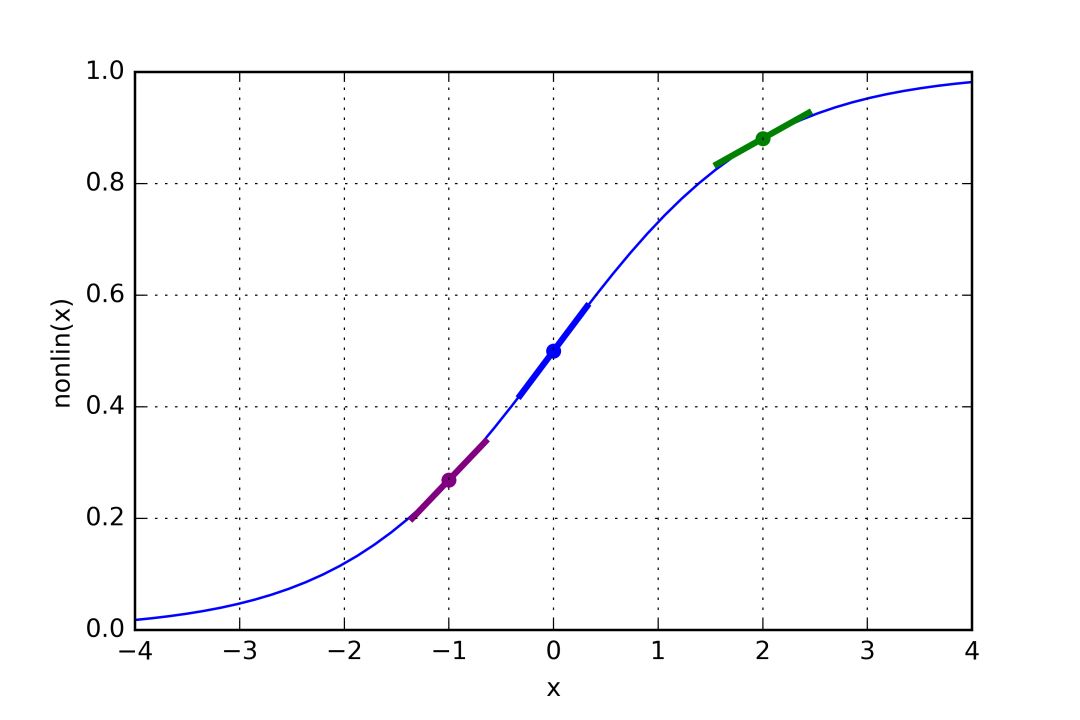
整个语句：误差加权导数

1. l1_delta = l1_error * nonlin(l1,True)

“误差加权导数”有数学上更精确的说法，但我觉得这个名字捕捉到了背后的直觉。l1_error是一个(4,1)矩阵。nonlin(l1, True)返回一个(4,1)矩阵。我们将它们逐元素相乘。这返回一个(4,1)矩阵l1_delta。

当我们将“斜率”乘以错误时，我们降低高信度预测的错误。再看一遍sigmoid图像！如果斜率实在很平缓（接近0），那么这个网络或者具有一个非常高的值，或者具有一个非常低的值。这意味着网络十分自信。然而，如果网络猜测的值接近(x=0, y=0.5)，那么它不是那么自信。我们更剧烈地更新那些缺乏信心的预测，同时倾向于通过乘以一个接近零的数字保留那些自信的预测。

行39： 一切就绪，我们可以更新网络了！让我们看下单个训练样本。

译者注：上图左侧标注L1、L2分别应为L0、L1

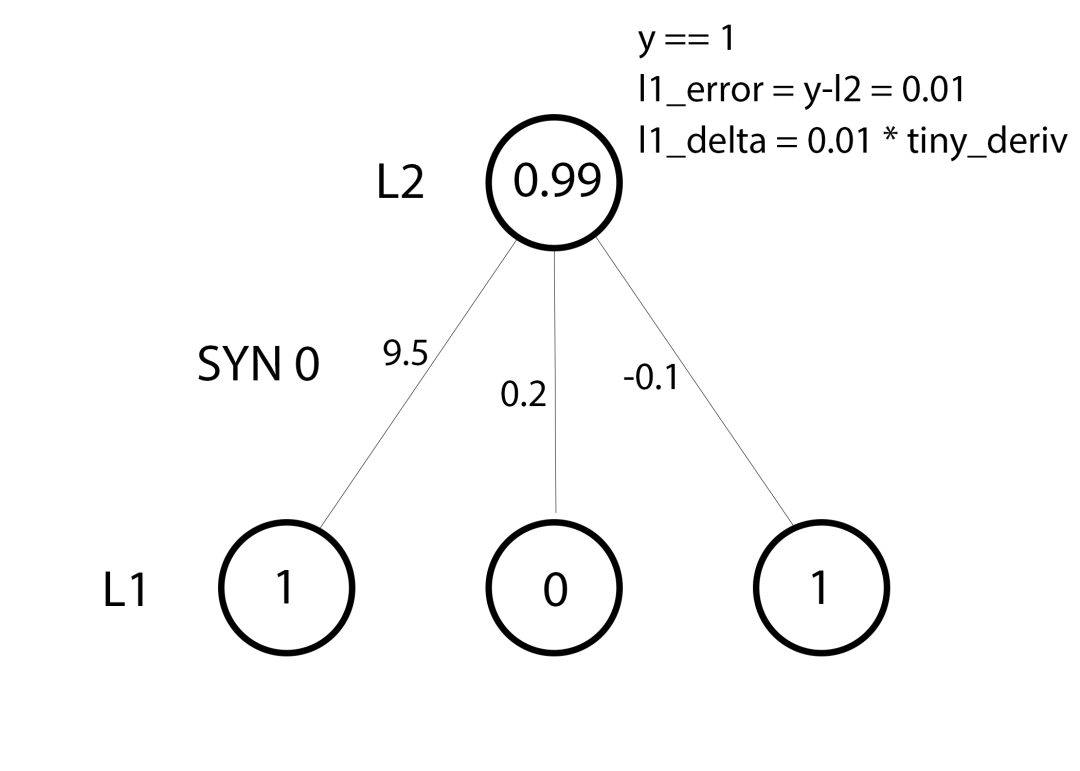
对这个样本而言，我们已经准备好更新权重了。让我们更新最左边的权重（9.5）。

1. weight_update = input_value * l1_delta

对最左边的权重而言，这将是1.0 * L1_delta。推测起来，这会非常轻微地增加9.5. 为什么只增加一点点？好吧，预测已经相当自信了，而且预测的结果也基本正确。低误差和低斜率意味着非常小的更新。考虑所有3个权重。这3个权重都将略微增加。

译者注：上图左侧标注L1、L2分别应为L0、L1

然而，因为我们使用“全batch”配置，我们将对所有4个训练样本执行上述操作。因此，这个过程更像上图所示。所以，第39行做了什么？它为每个训练样本的每个权重计算权重更新，累加起来，然后更新权重，这些都是在一行之内完成的。探索矩阵乘法，你将看到它是如何做到的！

奥秘

所以，既然我们已经了解网络是如何更新的，让我们回过头来看一下训练数据然后反思一下。当输入和输出都是1的时候，我们增加两者之间的权重。当输入是1、输出是0时，我们减少两者之间的权重。

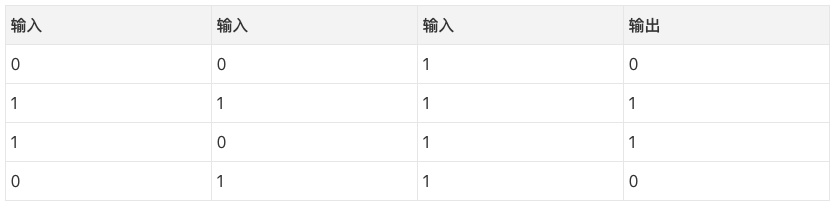
因此，在上表的4个训练样本中，第一个输入与输出之间的权重将持续增加或保持不变，而其他两个权重将发现自己在不同的样本上一会儿增加，一会儿下降（因而无法取得进展）。这一现象导致我们的网络基于输入和输出之间的相关性进行学习。

二、稍微加大难度

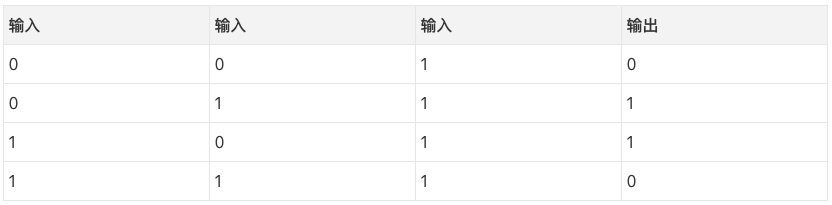
考虑基于三个输入栏预测输出栏。妙在没有一列和输出是相关的。每列有50%的机会预测1，50%的机会预测0.

那么，模式是什么呢？看起来结果完全和第三列无关，这一列的值永远是1. 然而，第1列和第2列组合起来看比较清楚。如果第1列和第2列有一列是1（但两列不同为1！），那么输出是1. 这是我们的模式。

这被认为是一个“非线性”模式，因为输入和输出之间没有直接的一一对应关系。相反，存在输入的组合和输出的一一对应关系，也就是第1列和第2列。

不管你信不信，图像识别是一个类似的问题。如果有100张尺寸相同的烟斗和自行车的图像，没有任何单独的像素位置和自行车或烟斗的存在性直接相关。从纯统计学角度看，像素可能是随机的。然而，特定的像素组合不是随机的，也就是说，像素的组合形成了自行车或烟斗的图像。

我们的策略

为了将我们的像素组合成和输出具有一一对应关系的东西，我们需要增加一个网络层。我们的第一层网络将组合输入，第二层网络以第一层网络的输出作为输入，并将其输入映射到输出。在我们跳到实现之前，先看下这个表格。

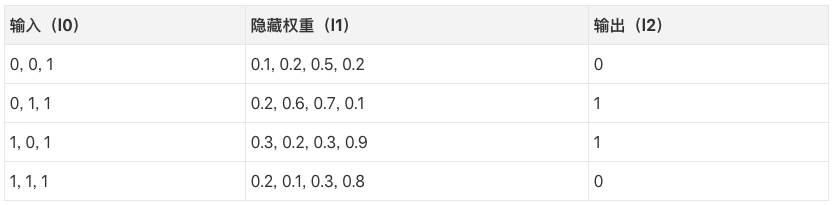
如果我们随机初始化权重，我们将得到如上表所示的l1的隐藏状态值。注意到没有？隐藏权重的第二项（第二个隐藏节点）与输出已经有隐约的相关性！它并不完美，但确实存在。信不信由你，这是神经网络训练中很重要的一部分。（一个有争议的观点认为这是神经网络训练的唯一方式。）下面的训练将放大这一相关性。它将同时更新syn1和syn0，更新syn1以便将隐藏权重映射到输出，更新syn0以便更好地基于输入产生权重！

注意：这个增加更多网络层以建模关系的更多组合的领域称为“深度学习”，得名自建模时采用的越来越深的网络层。

三层神经网络

1. importnumpyasnp

3. defnonlin(x,deriv=False):

4.    if(deriv==True):

5.        returnx*(1-x)

7.    return1/(1+np.exp(-x))

9. X = np.array([[0,0,1],

10.            [0,1,1],

11.            [1,0,1],

12.            [1,1,1]])

14. y = np.array([[0],

15.            [1],

16.            [1],

17.            [0]])

19. np.random.seed(1)

21. # 随机初始化权重（均值0）

22. syn0 =2*np.random.random((3,4)) -1

23. syn1 =2*np.random.random((4,1)) -1

25. forjinxrange(60000):

27.    # 前向传播，层0、1、2

28.    l0 = X

29.    l1 = nonlin(np.dot(l0,syn0))

30.    l2 = nonlin(np.dot(l1,syn1))

32.    # 离目标值还差多少？

33.    l2_error = y - l2

35.    if(j%10000) ==0:

36.        print"Error:"+ str(np.mean(np.abs(l2_error)))

38.    # 目标值在哪个方向？

39.    # 我们很确定吗？如果确定，不要改变太多。

40.    l2_delta = l2_error*nonlin(l2,deriv=True)

42.    # 根据权重 ，每个l1值对l2误差的贡献有多大？

43.    l1_error = l2_delta.dot(syn1.T)

45.    # 目标l1在哪个方向？

46.    # 我们很确定吗？如果确定，不要改变太多。

47.    l1_delta = l1_error * nonlin(l1,deriv=True)

49.    syn1 += l1.T.dot(l2_delta)

50.    syn0 += l0.T.dot(l1_delta)

1. Error:0.496410031903

2. Error:0.00858452565325

3. Error:0.00578945986251

4. Error:0.00462917677677

5. Error:0.00395876528027

6. Error:0.00351012256786

建议：在两块屏幕上打开本文，这样你就可以一边查看代码，一边阅读文章了。我写作下文的时候基本上就是这么做的。

所有的一切看起来应该很相似！这其实就是将2个之前的实现堆叠在一起。l1的输出是l2的输入。唯一不同的是第43行。

行43： 使用l2的“信度加权误差”来确立l1的误差。为了做到这一点，它简单地将权重间的误差从l2传给l1. 你可以把它的结果叫作“贡献加权误差”，因为我们学习l1中的每个节点对l2中的误差的“贡献”有多少。这一步骤称为“反向传播”，算法也是因此得名的。我们接着更新syn0，正如我们在双层实现中所做的那样。

三、结语和以后的工作

我的建议

如果你对神经网络的态度是严肃的，那我有一个建议。尝试基于回忆重建这个网络。我知道这也许听起来有点疯狂，但它切切实实很有帮助。如果你希望能够根据最新的学术论文创建任意的神经网络架构，或者阅读和理解不同架构的代码样例，我认为这是一个杀手级练习。即使你使用Torch、Caffe、Theano之类的框架，我仍然认为这是有用的。我在进行这一练习之前和神经网络打过好多年交道，这个练习是我在这一领域所做的最好的投资（而且它花不了多久）。

以后的工作

这个玩具例子仍然需要一些挂件才能真正解决当前最先进的架构。如果你打算进一步改进你的网络，下面是一些值得了解的概念。（也许我以后的文章会涉及其中部分内容。）

• Alpha

• Bias Units（偏置单元）

• Mini-Batches

• Delta Trimming

• Parameterized Layer Sizes（参数化的层尺寸）

• Regularization（正则化）

• Dropout

• Momentum（动量）

• Batch Normalization

• GPU兼容性

• 其他酷炫特性