

如何在图形生成过程中处理元素的对称性和排序,并提供可能的解决方案
电子说
描述
一般来说,图形是基本的数据结构,它在诸如知识图、物理和社会交互、语言和化学等许多重要的实际领域中对关系结构进行简明地捕捉。在本文中,我们引入了一种强大的新方法,用于学习图形中的生成式模型,既可以捕捉它们的结构也可以捕捉到属性。我们的方法使用图形神经网络表示图形节点和边缘之间的概率依赖关系,并且原则上来说,可以学习任何任意图形上的分布。经过一系列实验,我们的结果显示,一旦经过训练之后,我们的模型可以生成高质量的合成图和真实分子图的样本,无论是在无条件数据还是条件数据的情况下都是如此。与不使用图形结构表示的基线相比,我们的模型通常表现得更好。我们还探索了学习图形生成式模型过程中所存在的关键性挑战,例如,如何在图形生成过程中处理元素的对称性和排序,并提供可能的解决方案。可以这样说,我们的研究是用于学习任意图形上生成式模型的第一个方法,也是最为通用的方法,并且为从向量和序列式的知识表示,转向更有表现力和更灵活的关系数据结构,开辟了新的研究方向。
图形是许多问题域中信息的本质性表示。例如,知识图表和社交网络中的实体之间的关系可以很好地用图形进行表示,而且它们也适用于对物理世界进行建模,例如,分子结构以及物理系统中物体之间的交互。因此,捕捉特定图形族系分布的能力在实际生活中有很多应用。例如,从图形模型中进行采样可以致使发现新的配置,而这些配置所具有的全局属性与药物发现中所需要的是一样的(Gómez-Bombarelli等人于2016年提出)。要想获得自然语言句子中的图形结构语义表示(Kuhlmann和Oepen于2016年提出),需要具有能够在图上对(条件)分布进行建模的能力。图形上的分布还可以为图形模型的贝叶斯结构学习提供先验(Margaritis于2003年提出)。
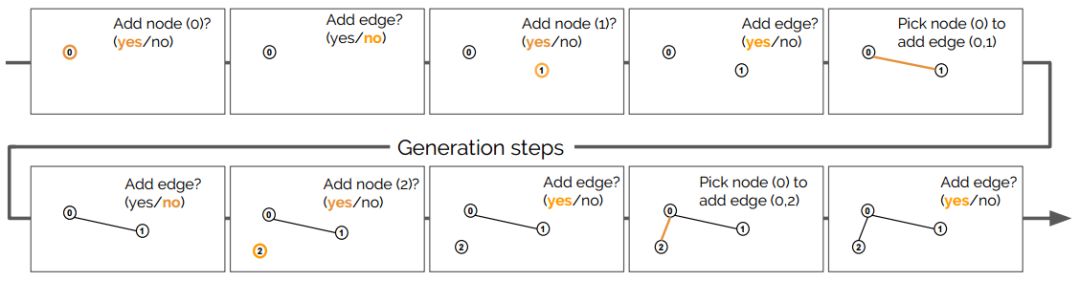
生成过程中所采取步骤的描述
我们至少从两个角度对图形的概率模型进行了广泛研究。一种方法是基于随机图形模型,将概率分配给大的图形类型(Erdos和Rényi于1960年、Barabási和Albert于1999年提出)。这些都具有很强的独立性假设,并且被设计成仅捕捉某些特定的图形属性,例如度数分布(degree distribution)和直径。虽然这些方法已被证明在对社交网络等领域进行建模时是有效的,但它们在更加丰富的结构化领域上应用还存在很大的挑战,其中,细微的结构差异在功能上可能是具有重要意义的,例如在化学中领域或自然语言中所表示的意义。
一个更具表现力但也更为脆弱的方法则是使用图形语法,它将机制从形式语言理论中泛化到非序列结构模型中(Rozenberg于1997年提出)。图语法是重写规则的系统,通过中间图的一系列转换递增地导出输出图。虽然符号图形语法(symbolic graph grammars)可以使用标准技术进行随机化或加权(Droste和Gastin于2007年提出),但从可学习性的观点来看,仍然存在两个需要解决的问题。首先,从一组未经注释的图形中引入语法是非常重要的,因为要想对可能用于构建图形的结构构建操作进行理解在算法上是很难进行的(Lautemann于1988年、Aguiñaga等人于2016年提出)。其次,与线性输出语法一样,图形语法在语言内容和要排除内容之间的区分上存在很大的困难,使得这种模型对于一些应用程序来说是不适合应用的,其中,它不适合将0概率分配给某些特定图形。
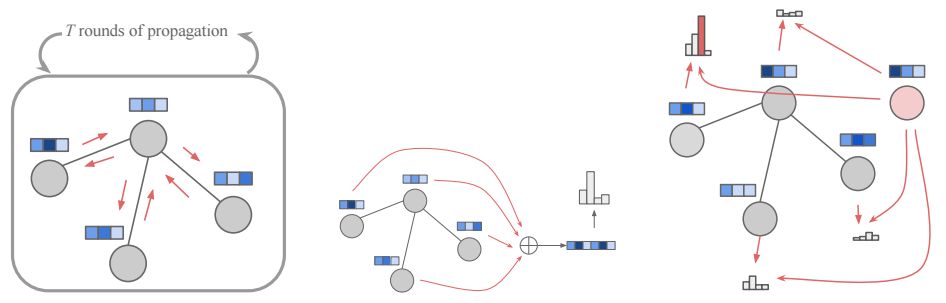
图形传播过程的示意图(左),节点选择 fnodes模块(右)
本文引入了一种新的、富有表现力的图形模型,它不需要做任何结构性假设,也避免了基于语法的技术的脆弱性。我们的模型以类似于图形语法的方式生成图形,其中在导出过程中,新结构(特别是新节点或新边缘)被添加到现有图形中,并且该添加事件的概率取决于图形导出的历史记录。为了在导出的每个步骤中对图形进行表示,我们使用一个基于图形结构的神经网络(图形网络)表示。最近,人们对于用于学习图形表示和解决图形预测问题的图形网络(graph nets)很感兴趣。这些模型是根据所利用的图形进行构造的,并且以独立于图形大小的方式进行参数化,因此针对同构图形具有不变性,从而为我们的研究目的提供了一个很好的匹配。
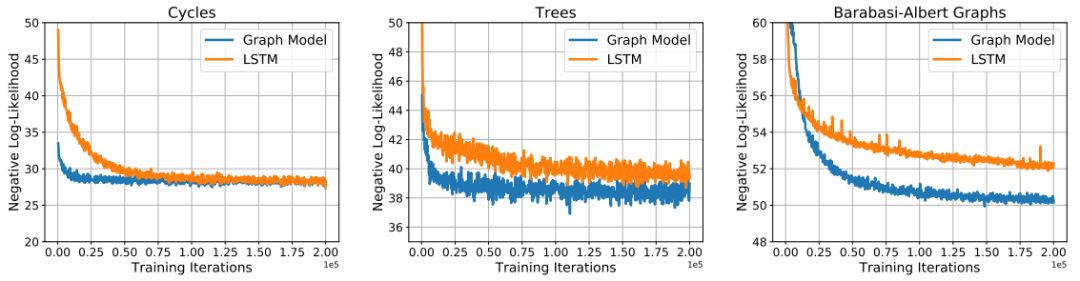
在三组数据集中对图形模型和LSTM模型进行训练的曲线
我们在生成具有某些常见拓扑性质(例如:周期性)的随机图形,和以非条件或条件的方式生成分子图形的任务中对我们的模型进行了评估。我们提出的模型在所有的实验中都表现良好,并且比随机图形模型(random graph models)和长短期记忆网络基线(LSTM baselines)获得了更好的结果。
本文所提出的是能够生成任意图形的强大模型。然而,这些模型依然面临着许多挑战。在本文中,我们将讨论未来会面临的一些挑战及可能的解决方案。
排序
节点和边缘的排序对于学习和评估而言都很重要,在实验中,我们总是使用预定义的分配方式排序。然而,通过将排序π视为潜在的变量来学习节点和边缘的排序也许是可能的,这在未来将是一个有趣的探索方向。
长序列
图形模型所使用的生成过程通常是一个长的决策序列,如果其他形式的图形线性化是可用的(例如:SMILES),那么这样的序列通常会缩短2-3倍。这对于图形模型而言是一个很大的劣势,这不仅难以获得准确的概率,还会使训练变得更加困难。为了缓解这一问题,我们可以调整图形模型,以便使其与问题域进行更多地关联,从而将多个决策步骤和循环转为单个步骤。
可扩展性
可扩展性是对本文所提出的图形生成模型的一个挑战。图形网络使用固定的传播步骤T来上传图形中的信息。然而,大的图形往往需要使用大量的T来获取足够的信息,这会限制这些模型的可扩展性。为了解决这一问题,我们可以使用依次扫描边缘的模型(Parisotto等人于2016年提出),或许采取一些由粗到精的生成方法。
训练难度
我们发现训练这样的图形模型要比训练典型的长短期记忆网络模型更为困难,这些模型所要进行训练的序列一般比较长,并且模型结构不断变化还会导致训练不稳定。降低学习速率可以解决很多不稳定问题,但通过调整模型可以获得更加令人满意的解决方案。
本文中,我们提出了一个强大的深度生成模型,其能够通过一个序列性过程生成任意形。我们在一些图形生成问题中对它的属性进行了研究。这一模型已经展现出很大的潜力,并且与标准LSTM模型相比具有独特的优势。我们希望我们的研究成果能够促进这方面的进一步研究,进而获得更好的图形生成模型。
-
通过交互式对称性校验提升集成电路设计流程2025-05-22 1413
-
运放的哪些参数可以反映出它的不对称性?2024-09-10 511
-
如何证明波导正规模的电场磁场具有时间对称性和反对称性?2023-10-19 1381
-
利用对称性化简求解对称电路2023-03-09 6727
-
关于麦克斯韦方程对称性的报告2022-11-07 1860
-
物质和反物质不对称性与CP对称性破缺2022-10-25 3114
-
对称性对傅里叶系数的影响2022-06-21 3044
-
关于电源排序的解决方案你了解吗2021-11-24 2932
-
对称性加密算法2021-07-19 1611
-
SHARC-Request评估码的DTS对称性2021-06-04 539
-
对称性对傅立叶系数的影响有哪些2019-09-01 6850
-
机械结构对称性实例设计2018-03-10 1242
-
晶体对称性分析2010-08-26 778
-
基于几何对称性的颅骨复原技术2009-04-14 653
全部0条评论

快来发表一下你的评论吧 !

