18个常用的强化学习算法整理：从基础方法到高级模型的理论技术与代码实现

颖脉Imgtec 2025-04-23 1310

描述

本来转自：DeepHub IMBA

本文系统讲解从基本强化学习方法到高级技术（如PPO、A3C、PlaNet等）的实现原理与编码过程，旨在通过理论结合代码的方式，构建对强化学习算法的全面理解。

为确保内容易于理解和实践，全部代码均在Jupyter Notebook环境中实现，仅依赖基础库进行算法构建。

代码库组织结构如下：

├── 1_simple_rl.ipynb ├── 2_q_learning.ipynb ├── 3_sarsa.ipynb ... ├── 9_a3c.ipynb ├── 10_ddpg.ipynb ├── 11_sac.ipynb ├── 12_trpo.ipynb ... ├── 17_mcts.ipynb └── 18_planet.ipynb

说明：github地址见文章最后，文章很长所以可以根据需求查看感兴趣的强化学习方法介绍和对应notebook。

搭建环境

首先，需要克隆仓库并安装相关依赖项：

# 克隆并导航到目录

git clone https://github.com/fareedkhan-dev/all-rl-algorithms.git

cd all-rl-algorithms

# 安装所需的依赖项

pip install -r requirements.txt

接下来，导入核心库：

# --- 核心Python库 ---

importrandom

importmath

fromcollectionsimportdefaultdict, deque, namedtuple

fromtypingimportList, Tuple, Dict, Optional, Any, DefaultDict# 用于代码中的类型提示

# --- 数值计算 ---

importnumpyasnp

# --- 机器学习框架（PyTorch - 从REINFORCE开始广泛使用） ---

importtorch

importtorch.nnasnn

importtorch.optimasoptim

importtorch.nn.functionalasF

fromtorch.distributionsimportCategorical, Normal# 用于策略梯度、SAC、PlaNet等

# --- 环境 ---

# 用于加载标准环境，如Pendulum

import gymnasium as gym

# 注意：SimpleGridWorld类定义需要直接包含在代码中

# 因为它是博客文章中定义的自定义环境。

# --- 可视化（由博客中显示的图表暗示） ---

importmatplotlib.pyplotasplt

importseabornassns# 经常用于热力图

# --- 可能用于异步方法（A3C） ---

# 尽管在代码片段中没有明确展示，但A3C实现通常使用这些

# import torch.multiprocessing as mp # 或标准的'multiprocessing'/'threading'

# --- PyTorch设置（可选但是好习惯） ---

device=torch.device("cuda"iftorch.cuda.is_available() else"cpu")

print(f"Using device: {device}")

# --- 禁用警告（可选） ---

importwarnings

warnings.filterwarnings('ignore') # 抑制潜在的废弃警告等

强化学习环境设置

虽然OpenAI Gym库提供了常见的强化学习环境，但为了深入理解算法核心原理，我们将自行实现大部分环境。仅在少数需要特殊环境配置的算法中，才会使用Gym模块。

本文主要关注两个环境：

自定义网格世界（从头实现）

钟摆问题（使用OpenAI Gymnasium）

# -------------------------------------

# 1. 简单自定义网格世界

# -------------------------------------

classSimpleGridWorld:

""" 一个基本的网格世界环境。 """

def__init__(self, size=5):

self.size=size

self.start_state= (0, 0)

self.goal_state= (size-1, size-1)

self.state=self.start_state

# 动作: 0:上, 1:下, 2:左, 3:右

self.action_map= {0: (-1, 0), 1: (1, 0), 2: (0, -1), 3: (0, 1)}

self.action_space_size=4

defreset(self) ->Tuple[int, int]:

""" 重置到初始状态。 """

self.state=self.start_state

returnself.state

defstep(self, action: int) ->Tuple[Tuple[int, int], float, bool]:

""" 执行一个动作，返回next_state, reward, done。 """

ifself.state==self.goal_state:

returnself.state, 0.0, True# 在目标处停留

# 计算潜在的下一个状态

dr, dc=self.action_map[action]

r, c=self.state

next_r, next_c=r+dr, c+dc

# 应用边界（如果碰到墙壁则原地不动）

ifnot (0<=next_r<self.sizeand0<=next_c<self.size):

next_r, next_c=r, c# 保持在当前状态

reward=-1.0 # 墙壁惩罚

else:

reward=-0.1 # 步骤成本

# 更新状态

self.state= (next_r, next_c)

# 检查是否达到目标

done= (self.state==self.goal_state)

ifdone:

reward=10.0 # 目标奖励

returnself.state, reward, done

SimpleGridWorld环境是一个基础的二维网格强化学习环境，智能体需要从起始位置(0,0)导航至目标位置(size-1, size-1)。智能体可以执行四个基本方向的移动动作（上、下、左、右），在每一步会接收一个小的步骤惩罚（-0.1），碰撞墙壁则会获得更大的惩罚（-1.0），而到达目标则给予较大的奖励（10.0）。

# -------------------------------------

# 2. 加载Gymnasium钟摆

# -------------------------------------

pendulum_env=gym.make('Pendulum-v1')

print("Pendulum-v1 environment loaded.")

# 重置环境

observation, info=pendulum_env.reset(seed=42)

print(f"Initial Observation: {observation}")

print(f"Observation Space: {pendulum_env.observation_space}")

print(f"Action Space: {pendulum_env.action_space}")

# 执行随机步骤

random_action=pendulum_env.action_space.sample()

observation, reward, terminated, truncated, info=pendulum_env.step(random_action)

done=terminatedortruncated

print(f"Step with action {random_action}:")

print(f" Next Obs: {observation}\n Reward: {reward}\n Done: {done}")

# 关闭环境（如果使用了渲染则很重要）

pendulum_env.close()

对于钟摆问题，我们使用Gymnasium库中的Pendulum-v1环境，这是一个基于物理的连续控制任务。上述代码初始化环境并展示了基本交互过程，包括获取初始观察、显示观察空间和动作空间的结构，以及执行一个随机动作并处理反馈。

让我们可视化这两个环境：

学习算法

网格世界和钟摆

从上图可以看出，在网格世界环境中，智能体的目标是找到从起点到目标的最短路径；而在钟摆环境中，目标是将摆杆从任意初始位置控制到竖直向上的平衡点。

1、最简单的强化学习算法

首先从强化学习的基础概念出发，即智能体与环境交互的循环过程。即使是最基本的方法也遵循这一交互模式。

以下图示展示了强化学习智能体的基本工作原理：

学习算法

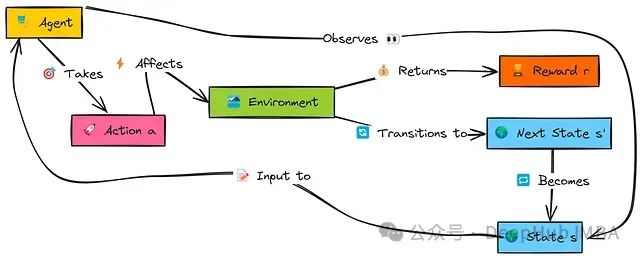
在这个交互流程中，智能体首先观察环境的当前状态s。基于该状态，智能体依据其当前策略决定执行一个动作a。该动作会影响环境，使环境转移到一个新状态s'，并向智能体提供一个数值奖励r，指示动作的即时效果。智能体利用这一反馈信息（s, a, r, s'）学习或调整其策略，然后从新状态s'继续交互循环。

我们将实现的第一个智能体与后续算法不同，它不会进行真正的"学习"，而是通过记录在特定状态下执行特定动作所获得的即时奖励来做决策。其目标很简单：在给定状态时，选择过去在该状态中平均即时奖励最高的动作。该方法没有考虑长期后果的概念。

首先，我们需要一个数据结构来存储智能体的记忆，采用一个将(状态,动作)对映射到接收奖励列表的嵌套字典：

# 记忆结构：memory[(state_tuple)][action_index] -> [list_of_rewards]

agent_memory: DefaultDict[Tuple[int, int], DefaultDict[int, List[float]]] = \

defaultdict(lambda: defaultdict(list))

# 示例：存储在状态(0,0)中采取动作1的奖励

# agent_memory[(0,0)][1].append(-0.1)

这个简单的字典结构能够存储每个状态-动作对的所有即时奖励记录。

接下来，智能体需要一个策略来选择其下一个动作。我们将基于记忆中存储的平均即时奖励，实现一个ε-贪心方法：

defchoose_simple_action(state: Tuple[int, int],

memory: DefaultDict[Tuple[int, int], DefaultDict[int, List[float]]],

epsilon: float,

n_actions: int) ->int:

""" 基于平均即时奖励使用epsilon-greedy选择动作。 """

ifrandom.random() <epsilon:

returnrandom.randrange(n_actions) # 探索

else:

# 利用：找到具有最佳平均即时奖励的动作

state_action_memory=memory[state]

best_avg_reward=-float('inf')

best_actions= []

foraction_idxinrange(n_actions):

rewards=state_action_memory[action_idx]

# 如果从这个状态从未尝试过这个动作，将其平均奖励视为0或非常低

avg_reward=np.mean(rewards) ifrewardselse0.0

ifavg_reward>best_avg_reward:

best_avg_reward=avg_reward

best_actions= [action_idx]

elifavg_reward==best_avg_reward:

best_actions.append(action_idx)

# 如果没有动作有积极奖励或状态未访问，随机选择

ifnotbest_actions:

returnrandom.randrange(n_actions)

# 随机打破平局

returnrandom.choice(best_actions)

该函数使智能体可以在随机探索（以概率ε）和利用已知信息之间进行平衡。当选择利用时，智能体会选择在历史记录中平均即时奖励最高的动作。

最后，"学习"步骤仅仅是在执行动作后更新记忆：

defupdate_simple_memory(memory: DefaultDict[Tuple[int, int], DefaultDict[int, List[float]]],

state: Tuple[int, int],

action: int,

reward: float) ->None:

""" 为状态-动作对添加接收到的奖励到记忆中。 """

memory[state][action].append(reward)

这个简单的智能体仅记录即时结果，没有考虑长期回报或累积奖励，这是我们将通过后续算法解决的主要局限性。

下面通过可视化来分析该智能体的学习过程及表现：

学习算法

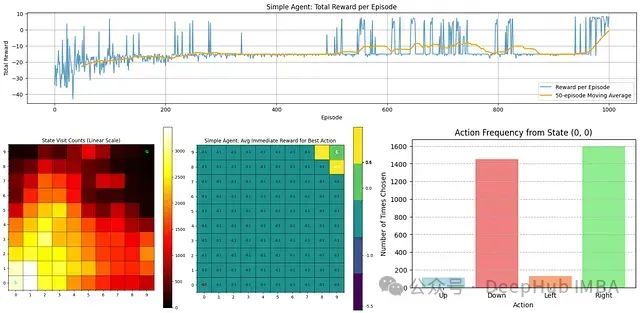
从上图可以观察到几个关键点：

奖励趋势：顶部图表显示了每个回合的总奖励。在早期阶段，智能体表现不佳（获得负奖励），但随着时间推移，其性能逐渐改善，这从移动平均线（橙色）的上升趋势可以明确看出。

状态访问频率：左下角热力图显示了智能体访问各个状态的频率。靠近起点的区域颜色较亮，表明探索集中在这些区域，而目标状态（G）的访问频率相对较低。

最佳动作奖励估计：中间热力图表示智能体对每个状态中最佳动作的即时奖励估计。大部分值较低，除了给予高奖励的目标状态附近区域。

动作选择分布：右下角条形图显示了智能体从起始状态(0,0)最常选择的动作。数据表明智能体倾向于向右和向下移动，这与通向目标的最优路径方向一致。

通过增加训练回合数，可以进一步提高智能体的寻路能力和性能。接下来，我们将介绍更为先进的Q学习算法。

2、Q学习

简单的记忆型智能体受限于只考虑即时奖励。Q学习则向前迈进了重要一步，它学习的是在一个状态中执行特定动作的"质量"或Q值，不仅考虑即时奖励，还考虑期望获得的总折扣未来奖励。

Q学习的目标是学习最优动作值函数 Q*(s,a)。

学习算法

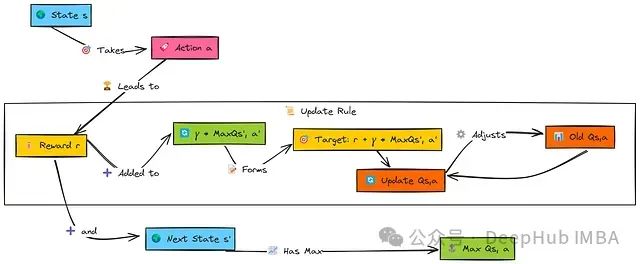
当智能体在状态s中执行动作a后，收到奖励r并转换到状态s'。为了更新原始(s,a)对的值，Q学习考虑了下一状态s'中所有可能动作a'的最佳Q值，表示为max Q(s', a')。

这个最大未来值经过因子γ(gamma)折扣后，与即时奖励r相加构成目标值。然后，原始(s,a)对的Q值通过学习率α(alpha)向这个目标值小幅调整。

学习通过以下更新规则进行：

学习算法

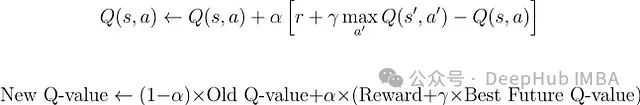
这意味着：

我们计算一个新的值估计：当前奖励 + 折扣因子 * 最佳未来值

计算这个新估计与当前Q值之间的差异（称为时序差分误差）

按照学习率确定的比例更新当前Q值

首先，我们初始化Q表，使用defaultdict可以简化实现，将未知的Q值默认初始化为0：

# Q表：q_table[(state_tuple)][action_index] -> q_value

q_table: DefaultDict[Tuple[int, int], Dict[int, float]] = \

defaultdict(lambda: defaultdict(float))

# 示例：访问Q((0,0), 0=Up)将初始返回0.0

# print(q_table[(0,0)][0])

这个结构存储了每个状态内每个动作的估计Q值。

动作选择仍然使用epsilon-greedy，但现在它基于学习到的Q值来利用，而不仅仅是即时奖励。

# 基于Q值的Epsilon-Greedy动作选择

defchoose_q_learning_action(state: Tuple[int, int],

q_table: DefaultDict[Tuple[int, int], Dict[int, float]],

epsilon: float,

n_actions: int) ->int:

""" 基于Q表值使用epsilon-greedy选择动作。 """

ifrandom.random() <epsilon:

returnrandom.randrange(n_actions) # 探索

else:

# 利用：选择该状态下Q值最高的动作

q_values_for_state=q_table[state]

ifnotq_values_for_state: # 如果状态未被访问/更新

returnrandom.randrange(n_actions)

max_q=-float('inf')

best_actions= []

# 遍历可用动作（0到n_actions-1）

foraction_idxinrange(n_actions):

q_val=q_values_for_state[action_idx] # defaultdict如果键缺失则返回0

ifq_val>max_q:

max_q=q_val

best_actions= [action_idx]

elifq_val==max_q:

best_actions.append(action_idx)

returnrandom.choice(best_actions) # 随机打破平局

智能体会以概率epsilon进行随机探索，否则选择当前状态下估计长期回报最高的动作。

Q学习的核心更新函数实现了贝尔曼方程更新：

# Q学习更新规则

defupdate_q_value(q_table: DefaultDict[Tuple[int, int], Dict[int, float]],

state: Tuple[int, int],

action: int,

reward: float,

next_state: Tuple[int, int],

alpha: float, # 学习率

gamma: float, # 折扣因子

n_actions: int,

is_done: bool) ->None:

""" 执行单个Q学习更新步骤。 """

# 获取当前Q值估计

current_q=q_table[state][action]

# 找到下一个状态的最大Q值（Q学习特有）

# 这代表了从下一个状态可达到的最佳可能值。

max_next_q=-float('inf')

ifnotis_doneandq_table[next_state]: # 检查next_state是否有条目

max_next_q=max(q_table[next_state].values())

elifis_done:

max_next_q=0.0# 如果回合结束，则无未来奖励

else:

max_next_q=0.0# 如果next_state还没有条目

# 计算TD目标：R + gamma * max(Q(s', a'))

td_target=reward+gamma*max_next_q

# 计算TD误差：TD目标 - Q(s, a)

td_error=td_target-current_q

# 更新Q值：Q(s, a) <- Q(s, a) + alpha * TD_Error

q_table[state][action] =current_q+alpha*td_error

该函数根据即时奖励和下一状态的最大Q值（这是Q学习的脱策略特性）计算目标值，然后更新实际执行的状态-动作对的Q值。

学习算法

从上图可以看出Q学习的效果：

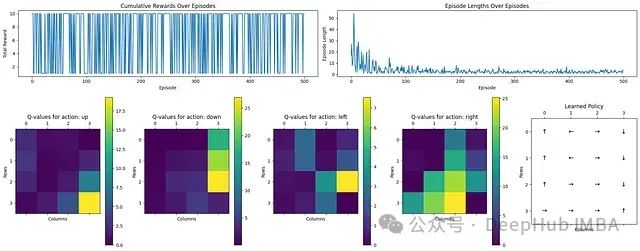
奖励和回合长度：顶部图表显示了随时间变化的累积奖励和回合长度。初始阶段，回合较长，表明智能体在探索低效路径。随着学习进行，回合长度明显减少，表明学习进程有效。

动作Q值分布：四个热力图展示了向上、下、左、右四个动作方向的Q值。黄色区域（高值）表示靠近目标状态的优先动作，而深色区域（低值）表示较不优化的选择。

学习策略可视化：最右侧的图表直观展示了最终学习到的策略，箭头指示各状态的最优动作方向，清晰地显示了通向目标的路径。

总体而言，通过Q学习，智能体成功学习了一条通向目标的最优路径。

3、Sarsa

SARSA（State-Action-Reward-State-Action，状态-动作-奖励-状态-动作）是另一种基于值的算法，与Q学习相似，但有一个关键区别：它是在策略的算法。

这意味着SARSA学习的是它当前正在遵循的策略的价值，包括任何探索性动作；而Q学习是脱策略的，它学习的是最优策略，不论当前采用何种探索策略。

学习算法

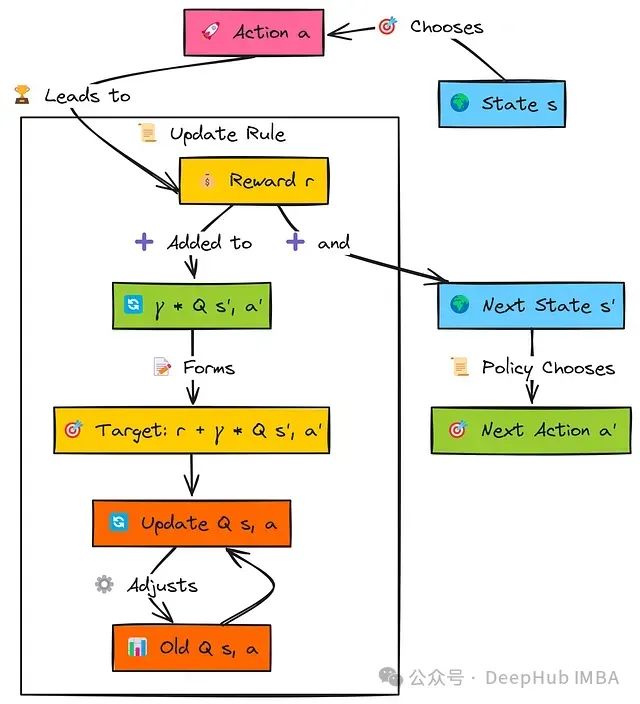
智能体从状态s开始，使用其策略选择动作a，获得奖励r并转换到状态s'。关键在于，在更新原始(s,a)对的值之前，智能体确定它将使用相同策略在状态s'中采取的下一个动作a'。

这个特定下一状态-动作对的Q值Q(s', a')经过因子γ折扣后与即时奖励r相加，构成SARSA目标。然后，原始的Q(s, a)按照学习率α的影响向这个目标值更新。这个过程遵循完整的五元组(s, a, r, s', a')，这也是算法名称的由来。

SARSA使用与Q学习相同的Q表结构存储状态-动作值，将状态-动作对映射到估计值。

动作选择通常也采用epsilon-greedy策略，与Q学习相同，以平衡探索和利用：

# Epsilon-Greedy动作选择（与Q学习相同的函数）

defchoose_sarsa_action(state: Tuple[int, int],

q_table: DefaultDict[Tuple[int, int], Dict[int, float]],

epsilon: float,

n_actions: int) ->int:

""" 基于Q表值使用epsilon-greedy选择动作。 """

ifrandom.random() <epsilon:

returnrandom.randrange(n_actions) # 探索

else:

# 利用：选择Q值最高的动作

q_values_for_state=q_table[state]

ifnotq_values_for_state:

returnrandom.randrange(n_actions)

max_q=-float('inf')

best_actions= []

foraction_idxinrange(n_actions):

q_val=q_values_for_state[action_idx] # 默认为0.0

ifq_val>max_q:

max_q=q_val

best_actions= [action_idx]

elifq_val==max_q:

best_actions.append(action_idx)

returnrandom.choice(best_actions) ifbest_actionselserandom.randrange(n_actions)

SARSA与Q学习的关键区别在于更新规则，它使用实际选择的下一个动作(a')的Q值，而非下一状态中可能的最大Q值：

# SARSA更新规则

defupdate_sarsa_value(q_table: DefaultDict[Tuple[int, int], Dict[int, float]],

state: Tuple[int, int],

action: int,

reward: float,

next_state: Tuple[int, int],

next_action: int, # 为下一步实际选择的动作

alpha: float,

gamma: float,

is_done: bool) ->None:

""" 执行单个SARSA更新步骤。 """

# 获取当前Q值估计

current_q=q_table[state][action]

# 获取*下一个状态和策略选择的下一个动作*的Q值

# 这是与Q学习的核心区别

q_next_state_action=0.0

ifnotis_done:

q_next_state_action=q_table[next_state][next_action] # 使用Q(s', a')

# 计算TD目标：R + gamma * Q(s', a')

td_target=reward+gamma*q_next_state_action

# 计算TD误差：TD目标 - Q(s, a)

td_error=td_target-current_q

# 更新Q值：Q(s, a) <- Q(s, a) + alpha * TD_Error

q_table[state][action] =current_q+alpha*td_error

由于SARSA在更新中使用Q(s',a')（下一个实际选择的动作的值，可能是探索性动作），相比Q学习，它倾向于学习更为保守的策略，特别是在存在潜在风险的环境中（如悬崖问题）。SARSA评估的是智能体当前积极遵循的策略。

学习算法

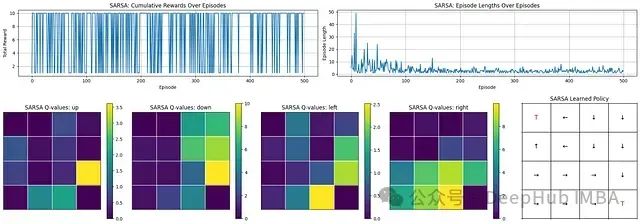
从SARSA的学习过程和结果可以观察到：

学习进展：回合长度显著减少，表明智能体学会了更高效地到达目标。

奖励表现：奖励总体较高但存在波动，反映了一个有效但不完全稳定的策略，这可能是由于持续的探索所致。

学习策略：Q值分布和最终策略图表显示智能体成功学习了指向目标状态('T')的动作序列。

综上所述，SARSA成功地学习了如何在环境中有效导航，提高了运行效率并频繁获得高奖励。最终的策略能够有效地引导智能体朝向目标，尽管性能上仍存在一定的变异性。

4、期望Sarsa

期望SARSA是在SARSA算法基础上的直接扩展，保持其在策略(on-policy)学习的核心特性，即基于当前策略所采取的动作进行价值函数的更新。

与标准SARSA依赖单一下一个动作（a'）进行更新不同，期望SARSA通过考虑后继状态中所有可能动作并按照当前策略π(a'∣s')的概率分布对其Q值进行加权平均，从而计算下一个状态的期望值。

这种期望计算机制有效降低了更新过程中的方差，相较于标准SARSA仅依赖可能包含探索噪声的单一动作样本。降低方差通常带来更平稳的价值估计收敛过程，并可能加速学习效率。

学习算法

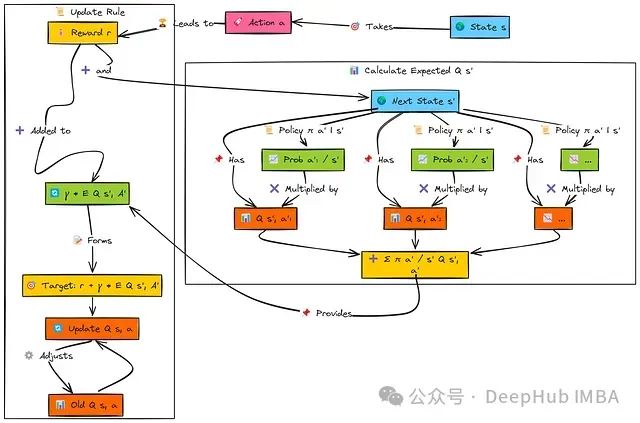
期望SARSA的基本过程与SARSA相似：智能体在状态's'中执行动作'a'，获取奖励'r'，并转移至后继状态's''。

然而在计算目标值时，期望SARSA考虑从's''可能执行的所有动作（'a'₁, 'a'₂, ...）。算法从当前策略中提取选择每个动作的概率（π(a'∣s')）以及相应的Q值Q(s',a')。

随后，算法通过将每个动作的选择概率与其对应Q值的乘积求和，计算状态's''的期望Q值：

学习算法

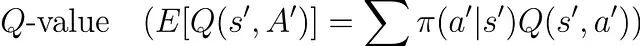
该期望值经折扣因子（γ）调整后与奖励'r'相加构成目标值。最后，根据学习率（α）将当前Q(s,a)向这个期望目标值方向更新。

Q表初始化函数和动作选择机制沿用了与SARSA部分相同的基于epsilon-greedy策略的实现。

期望SARSA的主要区别在于其更新规则，现在基于epsilon-greedy策略概率分布计算后继动作的期望值。

# 期望SARSA更新规则

defupdate_expected_sarsa_value(

q_table: DefaultDict[Tuple[int, int], Dict[str, float]],

state: Tuple[int, int],

action: int, # 现在使用整数动作索引

reward: float,

next_state: Tuple[int, int],

alpha: float,

gamma: float,

epsilon: float, # 计算期望值需要当前epsilon

n_actions: int,

is_done: bool

) ->None:

""" 执行单个期望SARSA更新步骤。 """

# 获取当前Q值估计

current_q=q_table[state][action]

# 计算下一个状态的期望Q值

expected_q_next=0.0

ifnotis_doneandq_table[next_state]: # 检查next_state是否存在且有条目

q_values_next_state=q_table[next_state]

ifq_values_next_state: # 检查字典是否非空

max_q_next=max(q_values_next_state.values())

# 找到所有最佳动作（处理平局）

best_actions= [afora, qinq_values_next_state.items() ifq==max_q_next]

# 在epsilon-greedy下计算概率

prob_greedy= (1.0-epsilon) /len(best_actions) # 将贪婪概率分配给最佳动作

prob_explore=epsilon/n_actions

# 计算期望值 E[Q(s', A')] = sum[ pi(a'|s') * Q(s', a') ]

fora_primeinrange(n_actions):

prob_a_prime=0.0

ifa_primeinbest_actions:

prob_a_prime+=prob_greedy# 添加贪婪概率

prob_a_prime+=prob_explore# 添加探索概率（适用于所有动作）

expected_q_next+=prob_a_prime*q_values_next_state.get(a_prime, 0.0) # 如果动作未见则默认为0

# TD目标: R + gamma * E[Q(s', A')]

td_target=reward+gamma*expected_q_next

# TD误差: TD目标 - Q(s, a)

td_error=td_target-current_q

# 更新Q值

q_table[state][action] =current_q+alpha*td_error

此更新函数考虑了epsilon-greedy策略的概率分布特性，在计算未来状态价值时，使更新过程对下一步可能选择的单一（可能随机）动作的敏感度降低，从而相比标准SARSA提供更稳定的学习过程。

学习算法

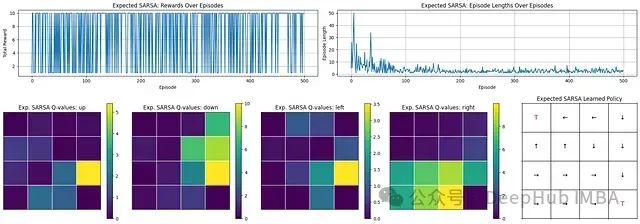
期望Sarsa

学习进展分析：回合长度迅速降低，表明智能体快速掌握了到达目标的高效路径。

奖励性能评估：初始学习阶段后，智能体能够频繁且稳定地获得接近10的高奖励值，证明其策略有效性。

学习策略分析：Q值矩阵清晰地识别出了首选动作，最终策略网格展示了智能体形成的合理路径，能够可靠地引导至终端状态（'T'）。

期望SARSA展现了强大且高效的学习能力，能够快速收敛至稳定策略。智能体获得持续高奖励的能力表明其学习到的策略具有稳定性和有效性。

5、Dyna Q

之前介绍的算法均为无模型方法，即仅从与环境的直接交互中学习。

Dyna-Q引入了一种简洁的基于模型强化学习框架，通过同时学习环境模型并利用该模型进行额外的"规划"步骤（模拟经验），有效加速学习过程。

核心理念在于更高效地利用每次真实交互经验：将其用于直接Q学习更新、内部模型更新，以及利用模型生成多次模拟未来场景并执行额外Q学习更新。

这种方法通常能显著提高样本效率，即从更少的真实环境交互中获取更快的学习速度。

学习算法

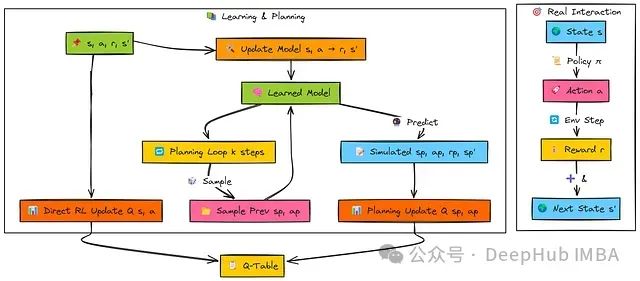
当智能体在状态s执行动作a并观测到奖励r与后继状态s'后，Dyna-Q算法并行执行三项任务：

直接强化学习（RL）：利用真实经验(s, a, r, s')更新Q值Q(s, a)，与标准Q学习算法相同。

模型学习：更新内部环境模型，记录状态s执行动作a导致奖励r和后继状态s'的转移关系。

规划：执行k次额外更新，每次随机选择先前经历过的状态-动作对(s_p, a_p)，查询学习到的模型获取预测奖励r_p和预测后继状态s_p'，然后使用这些模拟经验(s_p, a_p, r_p, s_p')执行Q学习更新。

Q表：维护Q(s,a)估计值。在最基本的表格形式中，这是一个字典结构，存储先前访问过的状态-动作对的观察结果（奖励和后继状态）：Model(s,a)→(r,s′)。

实现Dyna-Q需要定义Q表和模型的数据结构，以及一种追踪已访问状态-动作对用于规划的机制：

# Q表：q_table[(state_tuple)][action_index] -> q_value（与之前相同）

q_table_dynaq: DefaultDict[Tuple[int, int], Dict[int, float]] = \

defaultdict(lambda: defaultdict(float))

# 模型：model[(state_tuple, action_index)] -> (reward, next_state_tuple)

model_dynaq: Dict[Tuple[Tuple[int, int], int], Tuple[float, Tuple[int, int]]] = {}

# 跟踪已观察到的状态-动作对，用于规划期间的采样

observed_state_actions: List[Tuple[Tuple[int, int], int]] = []

动作选择仍然基于当前Q表使用epsilon-greedy策略。直接RL更新采用标准Q学习更新规则（在Q学习部分中详细介绍）。

算法的创新部分在于模型更新和规划步骤的实现。

首先，我们需要一个基于真实经验更新环境模型的函数：

# 模型更新函数

defupdate_model(model: Dict[Tuple[Tuple[int, int], int], Tuple[float, Tuple[int, int]]],

observed_pairs: List[Tuple[Tuple[int, int], int]],

state: Tuple[int, int],

action: int,

reward: float,

next_state: Tuple[int, int]) ->None:

""" 更新确定性表格模型和已观察对列表。 """

state_action= (state, action)

model[state_action] = (reward, next_state) # 存储结果

# 如果这个对之前未见过，则添加到列表中

ifstate_actionnotinobserved_pairs:

observed_pairs.append(state_action)

此函数简单记录状态-动作对及其结果转移信息。

规划步骤函数实现了从模型采样并应用Q学习更新的核心机制：

# 规划步骤函数

defplanning_steps(k: int, # 规划步骤数

q_table: DefaultDict[Tuple[int, int], Dict[int, float]],

model: Dict[Tuple[Tuple[int, int], int], Tuple[float, Tuple[int, int]]],

observed_pairs: List[Tuple[Tuple[int, int], int]],

alpha: float, gamma: float, n_actions: int) ->None:

""" 使用模型执行'k'次模拟Q学习更新。 """

ifnotobserved_pairs: # 没有观察就无法规划

return

for_inrange(k):

# 1. 采样随机先前观察到的状态-动作对

state_p, action_p=random.choice(observed_pairs)

# 2. 查询模型获取模拟结果

reward_p, next_state_p=model[(state_p, action_p)]

# 3. 使用模拟经验应用Q学习更新

# （假设模拟步骤不会结束回合，除非模型表示如此）

# 这里需要Q学习部分的update_q_value函数。

update_q_value(q_table, state_p, action_p, reward_p, next_state_p,

alpha, gamma, n_actions, is_done=False) # 在模拟中假设未结束

# （更复杂的模型可以预测'done'）

此规划函数利用从智能体学习的环境模型中采样的转移数据执行k次Q学习更新，实现了价值信息的更快传播。

学习算法

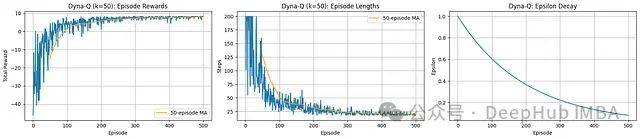
学习进展分析：观察到极为快速的收敛过程。回合长度迅速下降，表明智能体能够非常高效地学习到最优路径。

奖励性能分析：总奖励从初始负值陡峭上升至持续稳定的高正值，展示了快速有效的策略学习过程。

效率评估（Dyna-Q特性）：步数和奖励的快速改善明显体现了Dyna-Q规划机制（k=50）的优势，通过利用学习模型显著加速学习过程。

Dyna-Q算法展现了卓越的样本效率，使智能体能够迅速学习网格环境中的有效策略。规划组件促进了快速收敛至高奖励和短回合长度的优化目标。

6、Reinforce

我们现在将讨论从基于值的方法（Q学习，SARSA）转向基于策略的方法的重要转变。

REINFORCE算法不是学习动作值函数，而是直接学习和优化参数化策略π(a∣s;θ)，该策略将状态直接映射至动作概率分布，由参数集θ决定。策略参数调整的目标是使高质量动作（即导致高累积奖励的动作）具有更高的发生概率。

REINFORCE采用蒙特卡洛方法框架，这意味着算法在更新策略参数前需要收集完整回合的奖励序列。

学习算法

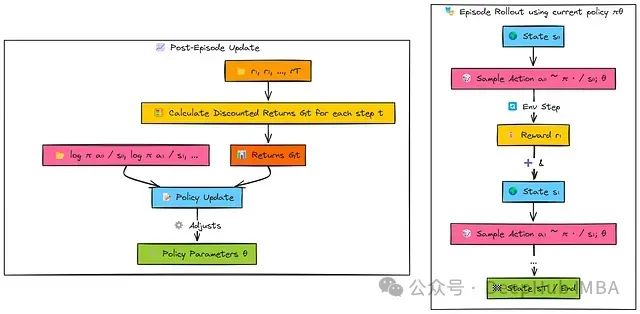
智能体使用当前策略网络（π_θ）生成一个完整回合的交互序列。在每个时间步骤，智能体：

基于当前状态s采样一个动作a。

存储该动作的对数概率（log π(a|s)）。

记录获取的奖励r。

回合完成后，智能体回顾分析整个奖励序列。算法计算从每个时间步t开始的折扣累积回报（G_t）。

最终，策略参数（θ）通过梯度上升进行更新：

对于后续获得高回报（G_t）的动作，更新过程增加其对数概率（log π(a|s)）。

对于后续获得低回报的动作，更新过程降低其对数概率。

首先，我们定义策略网络架构。该网络类似于Actor网络，通过Softmax层输出动作概率分布：

# 定义策略网络架构

classPolicyNetwork(nn.Module):

def__init__(self, n_observations: int, n_actions: int):

super(PolicyNetwork, self).__init__()

self.layer1=nn.Linear(n_observations, 128)

self.layer2=nn.Linear(128, 128)

self.layer3=nn.Linear(128, n_actions) # 输出logits

defforward(self, x: torch.Tensor) ->Categorical:

""" 前向传播，返回动作的Categorical分布。 """

ifnotisinstance(x, torch.Tensor):

x=torch.tensor(x, dtype=torch.float32, device=device) # 假设'device'已定义

elifx.dtype!=torch.float32:

x=x.to(dtype=torch.float32)

ifx.dim() ==1: x=x.unsqueeze(0)

x=F.relu(self.layer1(x))

x=F.relu(self.layer2(x))

action_logits=self.layer3(x)

# 直接从logits创建Categorical分布

returnCategorical(logits=action_logits)

该网络接收环境状态作为输入，并提供一种机制来采样动作并计算其对数概率。

接下来，动作选择函数利用策略网络采样动作并记录其对数概率：

# 通过采样选择动作

def select_action_reinforce(state: torch.Tensor, policy_net: PolicyNetwork) -> Tuple[int, torch.Tensor]:

""" 通过从策略网络的输出分布采样选择动作。 """

action_dist = policy_net(state)

action = action_dist.sample() # 采样动作

log_prob = action_dist.log_prob(action) # 获取所选动作的对数概率

return action.item(), log_prob

与epsilon-greedy策略不同，REINFORCE的探索机制是通过网络输出的概率分布采样过程自然引入的。

在回合结束后，需要计算每个时间步的折扣累积回报Gt：

# 计算折扣回报

defcalculate_discounted_returns(rewards: List[float], gamma: float, standardize: bool=True) ->torch.Tensor:

""" 计算每一步t的折扣回报G_t，可选择标准化。 """

n_steps=len(rewards)

returns=torch.zeros(n_steps, dtype=torch.float32) # 保持在CPU上进行计算

discounted_return=0.0

# 反向迭代

fortinreversed(range(n_steps)):

discounted_return=rewards[t] +gamma*discounted_return

returns[t] =discounted_return

ifstandardize:

mean_return=torch.mean(returns)

std_return=torch.std(returns) +1e-8# 添加epsilon以保持稳定

returns= (returns-mean_return) /std_return

returnreturns.to(device) # 最后移动到适当的设备

此函数计算回合中每个动作后的实际累积回报（Gt）。标准化处理能够提高训练稳定性。

最后，策略更新函数利用收集的对数概率和回报调整网络参数：

# 策略更新步骤

defoptimize_policy(log_probs: List[torch.Tensor],

returns: torch.Tensor,

optimizer: optim.Optimizer) ->float:

""" 执行一次REINFORCE策略梯度更新。 """

# 堆叠对数概率并确保回报具有正确的形状

log_probs_tensor=torch.stack(log_probs)

returns=returns.detach() # 在此更新中将回报视为固定目标

# 计算损失：- Sum(G_t * log_pi(a_t|s_t))

# 我们最小化负目标

loss=-torch.sum(returns*log_probs_tensor)

# 执行优化

optimizer.zero_grad()

loss.backward()

optimizer.step()

returnloss.item()

此函数计算REINFORCE算法的策略梯度损失，并使用优化器（如Adam）更新策略网络参数θ，使有利的动作序列在未来更可能出现。

学习算法

学习进展分析：智能体展现有效学习能力，从回合步骤（长度）的急剧减少并在低值稳定可以明确观察到。

奖励性能评估：总奖励从负值大幅提升并收敛到稳定的高正值，表明智能体成功学习了高效策略。

损失和稳定性分析：损失值在整个训练过程中表现出显著波动，移动平均线也未展示明确的收敛趋势。这突显了基本REINFORCE算法固有的高方差特性。

REINFORCE算法成功训练了智能体解决网格导航任务，实现了高奖励和高效路径规划。然而，从损失曲线的波动性可以看出，训练过程存在高方差现象，这是该算法的典型特征。

7、PPO（近端策略优化）

像REINFORCE这样的标准策略梯度方法可能存在训练不稳定性，因为基于噪声回报的单次更新可能导致策略发生剧烈变化，进而导致性能严重下降。

信任区域策略优化（TRPO）通过复杂的约束优化机制解决了这一问题。而近端策略优化（PPO）则提供了一种更为简洁的替代方案，通过使用裁剪的替代目标函数实现类似的稳定性。

PPO是一种演员-评论家、在策略算法，设计理念是在更新过程中确保新策略与旧策略保持适当的相似性，防止破坏性的大幅策略变化，同时保持高效学习能力，通常在同一批数据上进行多次迭代更新（epochs）。

学习算法

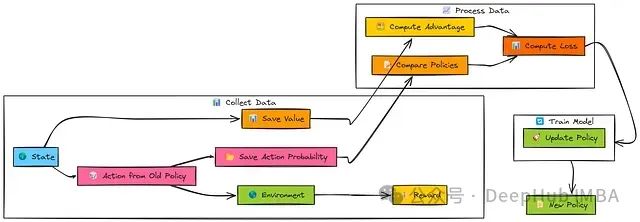
与REINFORCE和A2C类似，PPO首先使用当前的旧策略（π_old）收集一批经验数据(s, a, r, s')。算法同时存储每个动作在该策略下的对数概率。评论家网络（V_old）提供状态值估计。

在收集足够的经验数据后，计算优势估计（Â）—通常使用广义优势估计（GAE）方法。

PPO核心更新在这批收集的数据上进行多个epochs的迭代：

当前的新策略（π_new）对批次状态进行评估以获得新的动作对数概率。

计算新旧策略之间的概率比率r。

PPO应用裁剪目标（L_CLIP），基于裁剪参数（ϵ）限制r对更新的影响程度。

完整损失函数由以下组成部分构成：

裁剪的策略损失（L_CLIP），确保策略更新稳定性。

值函数损失（L_VF），优化评论家网络。

熵正则项（S），鼓励足够的探索行为。

演员（策略）和评论家（值函数）网络通过梯度下降基于此综合损失函数进行优化。

PPO使用与A2C和TRPO相同的Actor（策略网络）和Critic（值网络）架构。

算法通常采用相同的广义优势估计（GAE）函数计算优势值。PPO的独特之处在于其更新逻辑，特别是策略损失函数（L_CLIP）的计算方式。

学习算法

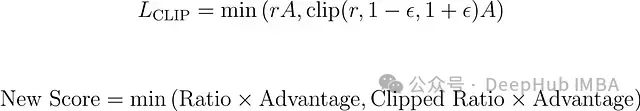
更新逻辑方程

# PPO更新步骤（简化视图，假设数据已批处理）

defupdate_ppo(actor: PolicyNetwork,

critic: ValueNetwork,

actor_optimizer: optim.Optimizer,

critic_optimizer: optim.Optimizer,

states: torch.Tensor,

actions: torch.Tensor,

log_probs_old: torch.Tensor, # 来自用于rollout的策略的对数概率

advantages: torch.Tensor, # 计算的GAE优势

returns_to_go: torch.Tensor, # 值函数的目标（Adv + V_old）

ppo_epochs: int, # 每批次的更新次数

ppo_clip_epsilon: float, # 裁剪参数ε

value_loss_coeff: float, # 评论家损失权重

entropy_coeff: float) ->Tuple[float, float, float]: # 平均损失

total_policy_loss=0.0

total_value_loss=0.0

total_entropy=0.0

# 数据在进入循环前应该被分离

advantages=advantages.detach()

log_probs_old=log_probs_old.detach()

returns_to_go=returns_to_go.detach()

# 在同一批次上执行多个epochs的更新

for_inrange(ppo_epochs):

# --- Actor（策略）更新 ---

policy_dist=actor(states) # 获取当前策略分布

log_probs_new=policy_dist.log_prob(actions) # 动作在*新*策略下的对数概率

entropy=policy_dist.entropy().mean() # 平均熵

# 计算比率r(θ) = π_new / π_old

ratio=torch.exp(log_probs_new-log_probs_old)

# 计算裁剪的替代目标部分

surr1=ratio*advantages

surr2=torch.clamp(ratio, 1.0-ppo_clip_epsilon, 1.0+ppo_clip_epsilon) *advantages

# 策略损失：-(min(surr1, surr2)) - entropy_bonus

policy_loss=-torch.min(surr1, surr2).mean() -entropy_coeff*entropy

# 优化actor

actor_optimizer.zero_grad()

policy_loss.backward()

actor_optimizer.step()

# --- Critic（值）更新 ---

values_pred=critic(states).squeeze() # 使用当前critic预测V(s)

value_loss=F.mse_loss(values_pred, returns_to_go) # 与计算的回报比较

# 优化critic

critic_optimizer.zero_grad()

(value_loss_coeff*value_loss).backward() # 在backward前缩放损失

critic_optimizer.step()

# 累积统计

total_policy_loss+=policy_loss.item()

total_value_loss+=value_loss.item()

total_entropy+=entropy.item()

# 返回epochs上的平均损失

returntotal_policy_loss/ppo_epochs, total_value_loss/ppo_epochs, total_entropy/ppo_epochs

此更新函数在收集的数据批次上进行多次迭代（epochs）。

在每次迭代中，函数计算策略比率，应用裁剪机制限制策略变化幅度，计算值函数损失，并更新两个网络参数。这种组合机制实现了稳定且高效的学习过程。

学习算法

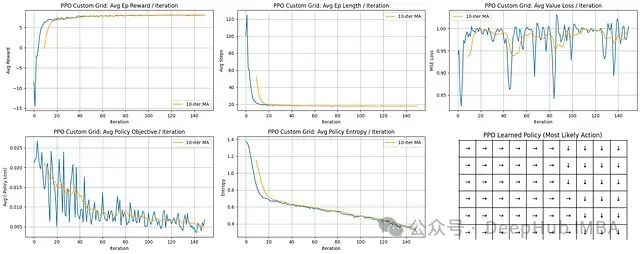
学习进展分析：PPO展示极为快速的学习能力；平均回合长度急剧下降并迅速稳定在较低水平。

奖励性能评估：平均奖励值呈陡峭上升趋势并稳定在接近最大可能值的水平，表明算法快速收敛到高效策略。

训练稳定性分析：策略目标（损失）和熵值均呈稳步下降趋势，表明策略持续改进并逐步减少探索。值函数损失虽有波动但整体保持在可控范围内。

学习策略评估：最终策略网格清晰展示了确定性且合理的导航路径，指向网格右下方的目标区域。

PPO算法表现卓越，特点是收敛速度快、学习过程稳定且能持续获得高奖励。智能体能够迅速学习形成高效且有效的网格环境导航策略。

8、A2C（同步优势演员-评论家）

同步优势演员-评论家（A2C）是演员-评论家算法族中的一个同步、简化变体。

与其他演员-评论家方法相似，A2C使用双网络架构：一个演员网络负责动作选择，一个评论家网络负责状态评估。A2C特别采用优势函数估计：

学习算法

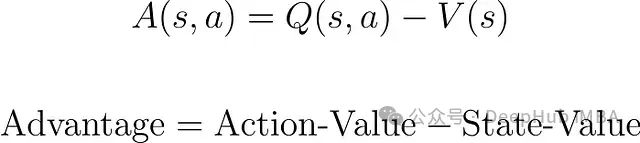
优势函数指导演员网络的更新过程，相比REINFORCE算法能够有效降低梯度估计的方差。

与其异步版本A3C不同，A2C执行同步参数更新。

算法通常在收集一批经验数据后（通常从并行环境收集，尽管本示例中按顺序模拟）才同时计算并应用梯度更新到演员和评论家网络参数。

学习算法

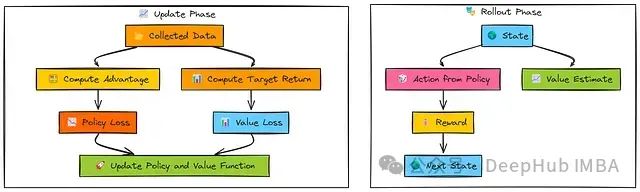
在交互采样阶段，演员网络（π_θ）根据当前状态（s）选择动作（a），而评论家网络（V_ϕ）估计该状态的价值（V(s)）。

执行动作后获得奖励（r）和后继状态（s'）。此过程重复N步，收集一批交互数据。

在参数更新阶段，收集的奖励序列和值估计用于计算目标回报（R_t）和优势估计（Â）。策略损失通过优势和动作对数概率计算，目标是增强具有正优势的动作概率。

值函数损失计算为预测值（V(s_t)）与目标回报（R_t）之间的均方误差。

最后，两种损失函数的梯度被计算并用于同步更新演员（θ）和评论家（ϕ）网络参数。

演员网络：策略函数π(a∣s;θ)，输出动作概率分布。

评论家网络：值函数V(s;ϕ)，估计状态价值。

优势函数：计算为Â_t≈R_t−V(s_t)，其中R_t通常是n步回报或通过GAE计算。它衡量动作相对于状态平均预期回报的相对优势。

同步更新机制：梯度在一批经验数据上计算并同时应用到演员和评论家网络。

A2C使用与PPO和TRPO相同的Actor（策略网络）和Critic（值网络）架构。

算法通常采用广义优势估计（GAE）计算优势值和评论家网络的目标回报。

A2C更新函数计算组合损失并同步应用梯度更新：

# A2C更新步骤

defupdate_a2c(actor: PolicyNetwork,

critic: ValueNetwork,

actor_optimizer: optim.Optimizer,

critic_optimizer: optim.Optimizer,

states: torch.Tensor,

actions: torch.Tensor,

advantages: torch.Tensor, # 计算的GAE优势

returns_to_go: torch.Tensor, # 值函数的目标（Adv + V_old）

value_loss_coeff: float, # 评论家损失权重

entropy_coeff: float # 熵奖励权重

) ->Tuple[float, float, float]: # 平均损失

# --- 评估当前网络 ---

policy_dist=actor(states)

log_probs=policy_dist.log_prob(actions) # 所采取动作的对数概率

entropy=policy_dist.entropy().mean() # 平均熵

values_pred=critic(states).squeeze() # 评论家的值预测

# --- 计算损失 ---

# 策略损失（演员）：- E[log_pi * A_detached] - entropy_bonus

policy_loss=-(log_probs*advantages.detach()).mean() -entropy_coeff*entropy

# 值损失（评论家）：MSE(V_pred, Returns_detached)

value_loss=F.mse_loss(values_pred, returns_to_go.detach())

# --- 优化演员 ---

actor_optimizer.zero_grad()

policy_loss.backward() # 计算演员梯度

actor_optimizer.step() # 更新演员权重

# --- 优化评论家 ---

critic_optimizer.zero_grad()

# 评论家损失的反向传播（缩放后）

(value_loss_coeff*value_loss).backward()

critic_optimizer.step() # 更新评论家权重

# 返回用于记录的损失（策略目标部分，值损失，熵）

returnpolicy_loss.item() +entropy_coeff*entropy.item(), value_loss.item(), entropy.item()

此函数接收一批交互数据，基于计算的优势估计和目标回报计算策略和值函数损失，然后对演员和评论家网络执行独立但同步的梯度更新。

学习算法

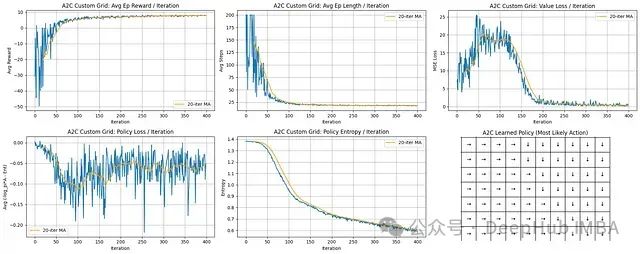
学习进展与效率分析：智能体展现出强劲的学习能力。平均回合奖励从显著负值迅速上升，在约100-150次迭代后稳定收敛在接近最大可能值水平。同时，平均回合长度从最大步数限制急剧下降至低且稳定的值，表明智能体迅速掌握了高效路径规划能力。

值函数学习过程：值损失（MSE）在初始阶段呈上升趋势，这是因为评论家网络需要在快速变化的策略环境中学习准确的状态价值。损失在约75次迭代后达到峰值，随后随着策略稳定而稳步下降，表明评论家网络对状态价值的预测精度显著提高。

策略优化与稳定性：策略损失曲线呈现一定噪声，这是策略梯度方法的固有特性，反映了更新过程中的方差。然而，移动平均趋势显示整体损失呈下降趋势（尽管有波动），表明策略持续改进。

最终策略评估：策略网格展示了一个连贯且确定性的导航策略。方向箭头一致地指引智能体，形成通向位于网格右下区域目标位置的明确路径，证明算法成功收敛到特定的导航方案。

A2C算法成功优化了策略网络（演员）和值函数网络（评论家），实现了快速收敛到高平均奖励和高效导航路径的目标，最终形成了清晰合理的策略决策模式。

9、A3C (异步优势演员-评论家算法)

异步优势演员-评论家算法(A3C)是一项突破性的强化学习方法，其创新之处在于通过并行化机制实现演员-评论家学习的稳定性，而无需依赖DQN中使用的经验回放缓冲区。

该算法部署多个并行执行的"工作者"智能体，每个工作者与环境的独立副本进行交互。

A3C的核心原理是基于异步更新机制：各工作者根据其本地经验独立计算参数更新，并将这些更新异步应用于共享的全局网络，无需相互协调或等待。

这种来自不同工作者的持续、多样化的更新流有效降低了训练数据间的相关性，从而显著提高了学习稳定性。

学习算法

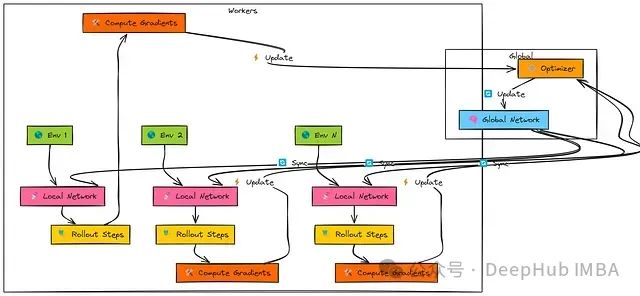
该算法架构中存在多个独立工作者。每个工作者首先从共享的"全局网络"复制参数。

随后，工作者使用其本地网络副本与专属环境实例交互，执行一系列步骤(即"n步展开")。

基于这段轨迹经验，工作者计算其本地网络中演员和评论家组件的梯度。

最后，工作者异步地将这些梯度传递给共享优化器，用于更新全局网络参数。

由于各工作者独立运行且在不同时间点进行更新，全局网络接收到的是具有多样性且相关性较低的更新流。

A3C的关键技术特点包括：

异步更新：工作者之间无需相互等待，减少了计算资源的闲置时间，同时降低了更新之间的数据相关性。

全局与本地网络架构：工作者定期与中央全局网络同步参数，但在本地进行梯度计算。

N步回报计算：更新通常基于短序列(n步)内收集的奖励总和，再加上由评论家网络对n步后状态的价值估计。这种方法平衡了单步时序差分学习的偏差与完整蒙特卡洛回报的方差。

优势估计：优势函数计算采用Â_t = R_t − V(s_t)公式，其中R_t表示n步回报。

A3C典型实现采用共享初层特征提取的组合演员-评论家网络架构：

# 共享的演员-评论家网络(与A2C结构相同)

classActorCriticNetwork(nn.Module):

def__init__(self, n_observations: int, n_actions: int):

super(ActorCriticNetwork, self).__init__()

self.layer1=nn.Linear(n_observations, 128)

self.layer2=nn.Linear(128, 128)

self.actor_head=nn.Linear(128, n_actions) # 动作对数概率

self.critic_head=nn.Linear(128, 1) # 状态价值

defforward(self, x: torch.Tensor) ->Tuple[Categorical, torch.Tensor]:

ifnotisinstance(x, torch.Tensor):

x=torch.tensor(x, dtype=torch.float32, device=x.device)

elifx.dtype!=torch.float32:

x=x.to(dtype=torch.float32)

ifx.dim() ==1: x=x.unsqueeze(0)

x=F.relu(self.layer1(x))

shared_features=F.relu(self.layer2(x))

action_logits=self.actor_head(shared_features)

state_value=self.critic_head(shared_features)

# 确保在添加批次维度的情况下值被压缩

ifx.shape[0] ==1andstate_value.dim() >0:

state_value=state_value.squeeze(0)

returnCategorical(logits=action_logits.to(x.device)), state_value

每个工作者收集n步经验并计算目标回报和优势值：

# 计算N步回报和优势(在每个工作者内使用)

defcompute_n_step_returns_advantages(rewards: List[float],

values: List[torch.Tensor], # 网络预测的V(s_t)

bootstrap_value: torch.Tensor, # V(s_{t+n})预测，已分离

dones: List[float], # 完成标志(0.0或1.0)

gamma: float

) ->Tuple[torch.Tensor, torch.Tensor]:

""" 计算n步回报(评论家目标)和优势(演员指导)。"""

n_steps=len(rewards)

returns=torch.zeros(n_steps, dtype=torch.float32) # 在CPU上存储结果

advantages=torch.zeros(n_steps, dtype=torch.float32)

# 分离用于优势计算的值(作为基线的一部分)

values_detached=torch.cat([v.detach() forvinvalues]).squeeze().cpu()

R=bootstrap_value.detach().cpu() # 从自举值开始

fortinreversed(range(n_steps)):

R=rewards[t] +gamma*R* (1.0-dones[t]) # 计算n步回报

returns[t] =R

# 确保values_detached具有正确的形状以进行优势计算

value_t=values_detachedifvalues_detached.dim() ==0elsevalues_detached[t]

advantages[t] =R-value_t# 优势 = N步回报 - V(s_t)

# 可选：标准化优势

# advantages = (advantages - advantages.mean()) / (advantages.std() + 1e-8)

returnreturns, advantages

工作者基于n步经验计算策略损失、价值损失和熵奖励，在本地计算梯度，并通过共享优化器异步更新全局网络参数：

# --- 工作者损失计算(概念性 - 由每个工作者执行) ---

# 假设'log_probs_tensor'、'values_pred_tensor'、'entropies_tensor'包含

# n步展开的网络输出，

# 而'returns_tensor'、'advantages_tensor'包含计算出的目标。

policy_loss=-(log_probs_tensor*advantages_tensor.detach()).mean()

value_loss=F.mse_loss(values_pred_tensor, returns_tensor.detach())

entropy_loss=-entropies_tensor.mean()

total_loss=policy_loss+value_loss_coeff*value_loss+entropy_coeff*entropy_loss

# --- 梯度应用(概念性) ---

global_optimizer.zero_grad()

total_loss.backward() # 计算本地模型上的梯度

# 将梯度从local_model.parameters()传输到global_model.parameters()

global_optimizer.step() # 将梯度应用于全局模型

这种异步更新机制使多个工作者能够并行贡献梯度更新，显著提高了多核系统上的训练时间效率。

学习算法

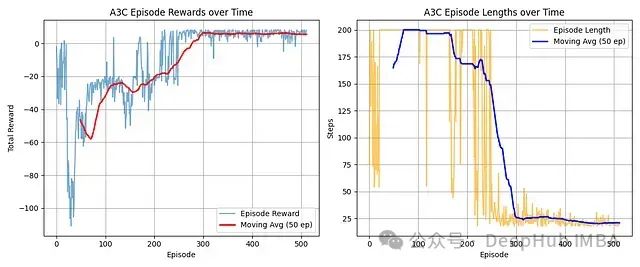
奖励进展：智能体从初始负分状态显著改善，移动平均线表明在约300回合后收敛至稳定的高正奖励水平。

效率提升：回合长度在250回合左右出现显著下降，从最大步数减少至稳定的较低平均值，表明任务完成效率大幅提高。

学习效果：图表清晰展示了A3C的有效学习过程，从初始探索/低效阶段转变为稳定高效的策略，持续有效地解决任务。

A3C算法成功学习了目标任务，展现了从初始低效表现到稳定高奖励水平的显著进步。

这一学习成效与效率的大幅提升紧密相关，从回合长度的快速下降可以明确观察到这一点。

智能体在大约300回合的训练后收敛到一个高质量且高效的策略。

10、DDPG (用于连续动作的演员-评论家算法)

深度确定性策略梯度(DDPG)是一种将演员-评论家方法扩展到连续动作空间环境的算法，适用于需要精确控制的任务(如施加特定扭矩、设定精确速度等)。

该算法巧妙地融合了DQN的核心技术(如经验回放缓冲区和目标网络)与确定性策略梯度方法。

DDPG的核心技术原理包括：

确定性演员网络：与REINFORCE/A2C/PPO等输出动作概率分布的算法不同，DDPG的演员网络直接为给定状态输出一个确定性动作向量。

Q值评论家网络：评论家网络学习状态-动作值函数Q(s, a)，类似于Q学习，但针对连续动作空间进行了适配，评估在状态(s)中执行演员选择的连续动作(a)的价值。

离策略学习：采用经验回放缓冲区存储交互经验并随机采样小批量数据进行学习，实现从历史数据中进行稳定学习，类似于DQN的机制。

目标网络机制：为演员和评论家网络均设置独立的目标网络，用于计算评论家的目标值，显著提高学习稳定性。

探索策略：由于算法采用确定性策略，需要手动添加探索机制，通常通过向演员网络输出动作添加噪声(如高斯噪声或奥恩斯坦-乌伦贝克过程噪声)实现。

学习算法

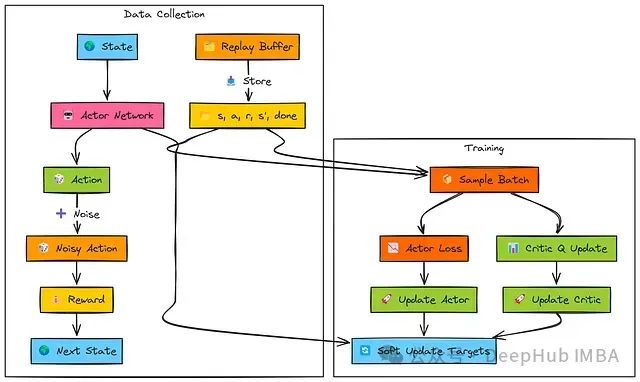
在环境交互阶段，演员网络基于当前状态(s)生成确定性动作。

为实现探索，在将动作传递给环境执行前，系统向该动作添加噪声。产生的转移经验(s, a, r, s', done)被存储到经验回放缓冲区中。

在训练阶段，系统从回放缓冲区中随机采样批量数据：

评论家网络更新：目标Q值(TD目标y)通过结合即时奖励(r)、目标演员和目标评论家网络对下一状态(s')的评估计算得出。主评论家网络计算当前批次状态和动作的Q(s, a)值。系统使用目标(y)与Q(s, a)之间的均方误差(MSE损失)更新主评论家网络参数(ϕ)。

演员网络更新：演员网络为批次状态(s)计算确定性动作。这些动作作为输入传递给主评论家网络以获取对应的Q值评估。演员网络通过最大化这些Q值(即最小化负Q值，L_θ = −Q)进行参数更新。

目标网络更新：目标演员和目标评论家网络(θ', ϕ')通过软更新机制逐步向主网络参数靠近，以平滑学习过程并提高稳定性。

DDPG实现需要设计独立的演员和评论家网络架构。演员网络输出确定性连续动作，通常使用tanh激活函数进行归一化和缩放：

# 简化的DDPG演员网络(输出连续动作)

classActorNetworkDDPG(nn.Module):

def__init__(self, state_dim: int, action_dim: int, max_action: float):

super(ActorNetworkDDPG, self).__init__()

self.layer1=nn.Linear(state_dim, 256)

self.layer2=nn.Linear(256, 256)

self.layer3=nn.Linear(256, action_dim)

self.max_action=max_action# 用于缩放输出

defforward(self, state: torch.Tensor) ->torch.Tensor:

x=F.relu(self.layer1(state))

x=F.relu(self.layer2(x))

# 使用tanh输出-1到1之间的值，然后缩放

action=self.max_action*torch.tanh(self.layer3(x))

returnaction

# 简化的DDPG评论家网络(接收状态和动作)

classCriticNetworkDDPG(nn.Module):

def__init__(self, state_dim: int, action_dim: int):

super(CriticNetworkDDPG, self).__init__()

# 分别或一起处理状态和动作

self.layer1=nn.Linear(state_dim+action_dim, 256)

self.layer2=nn.Linear(256, 256)

self.layer3=nn.Linear(256, 1) # 输出单个Q值

defforward(self, state: torch.Tensor, action: torch.Tensor) ->torch.Tensor:

# 连接状态和动作

x=torch.cat([state, action], dim=1)

x=F.relu(self.layer1(x))

x=F.relu(self.layer2(x))

q_value=self.layer3(x)

returnq_value

上述网络定义了DDPG的核心组件。演员网络学习"选择什么动作"，评论家网络学习"这些动作的价值评估"。

完整实现还需要经验回放缓冲区(类似DQN)和目标网络复制机制：

# 回放缓冲区(概念 - 使用deque或list)

# 目标网络(概念 - 创建演员/评论家的副本)

target_actor=ActorNetworkDDPG(...)

target_critic=CriticNetworkDDPG(...)

target_actor.load_state_dict(actor.state_dict()) # 初始化

target_critic.load_state_dict(critic.state_dict())

DDPG的核心更新逻辑涉及计算演员和评论家网络的损失函数，并对目标网络实施软更新：

# --- DDPG更新逻辑概述 ---

# (假设优化器已定义: actor_optimizer, critic_optimizer)

# (假设tau: 软更新率, gamma: 折扣因子已定义)

# 1. 从replay_buffer采样批次: states, actions, rewards, next_states, dones

# --- 评论家更新 ---

# 从目标演员获取下一动作: next_actions = target_actor(next_states)

# 从目标评论家获取目标Q值: target_q = target_critic(next_states, next_actions)

# 计算TD目标: td_target = rewards + gamma * (1 - dones) * target_q

# 获取当前Q值估计: current_q = critic(states, actions)

# 计算评论家损失(MSE): critic_loss = F.mse_loss(current_q, td_target.detach())

# 更新评论家:

critic_optimizer.zero_grad()

critic_loss.backward()

critic_optimizer.step()

# --- 演员更新 ---

# 从主演员获取当前状态的动作: actor_actions = actor(states)

# 计算演员损失(主评论家的负Q值): actor_loss = -critic(states, actor_actions).mean()

# 更新演员:

actor_optimizer.zero_grad()

actor_loss.backward()

actor_optimizer.step()

# --- 软更新目标网络 ---

soft_update(target_critic, critic, tau)

soft_update(target_actor, actor, tau)

这一实现框架展示了DDPG如何结合离策略学习、目标网络和双网络架构，实现连续动作空间中的有效强化学习。

实际应用中，智能体与环境交互时需要为演员网络输出动作添加适当噪声以促进探索。

学习算法

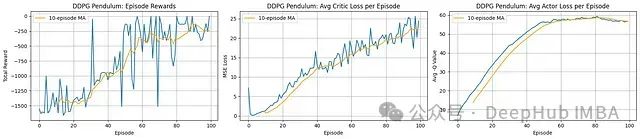
奖励进展：智能体展现出明确的学习过程。每回合总奖励(左图)从极低水平(约-1500)开始稳步提升，移动平均线在约100回合处达到-250左右的水平。这表明在控制钟摆以最小化成本函数方面取得了显著进步。尽管性能曲线存在波动，但整体呈现明显的正向趋势。

评论家学习：平均评论家损失(中图)在整个训练过程中呈现稳步增长趋势。这一现象在直觉上可能令人困惑，但在DDPG框架中，随着演员性能提升并探索到更高价值状态，目标Q值也相应增加。评论家网络不断适应这些演化的更高价值目标，因此损失增加实际上可能与学习成功同步发生，反映了价值函数适应过程中规模/复杂度的增加。

演员学习：平均演员"损失"(右图，标记为Avg -Q Value，实际表示演员实现的平均Q值)呈现明显的上升趋势，与奖励进展高度相关。这表明演员成功学习选择评论家评估为高价值(低成本)的动作，推动整体性能提升。图表末端的平缓趋势暗示学习可能正在趋于收敛。

DDPG算法成功地学习了钟摆控制任务，在约100回合的训练过程中显著提高了累积奖励。演员网络(负责选择最优动作)和评论家网络(负责评估状态-动作价值)均展现出有效的学习特征，尽管评论家损失增加是这类算法中常见的现象，反映了价值函数适应过程的复杂性。

11、SAC (最大熵演员-评论家算法)

软演员-评论家(SAC)是一种先进的演员-评论家架构算法，专为连续动作空间任务设计，在DDPG和TD3的基础上引入了最大熵强化学习框架。

该算法的独特之处在于智能体不仅被激励最大化累积奖励，还同时被鼓励维持尽可能高的策略熵(最大化动作随机性)。

这种熵最大化机制促进了更全面的环境探索，提高了算法的鲁棒性，并与DDPG相比，通常能实现更快速、更稳定的学习过程。与DDPG类似，SAC也采用离策略学习框架，利用经验回放缓冲区。

学习算法

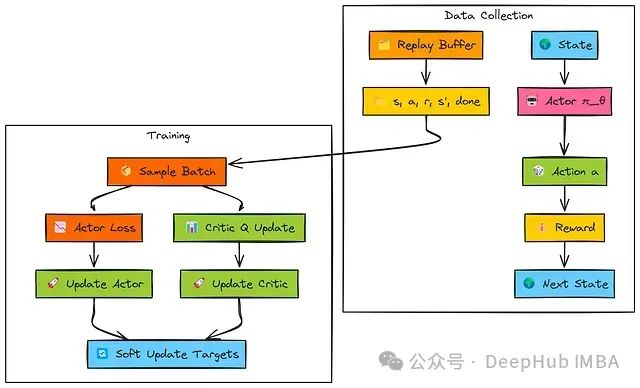
在环境交互阶段，与其他演员-评论家方法相似，但SAC的演员(π_θ)采用随机策略 – 输出一个动作概率分布，系统从中采样具体动作。交互产生的经验(s, a, r, s', done)存储于回放缓冲区中。

在训练阶段(从缓冲区采样批次数据):

评论家网络更新：SAC采用特殊的Q值目标计算方法。系统使用目标网络获取对从当前策略(在下一状态s'评估)采样的下一动作(a')的最小Q值估计(Min Q')。

随后从该最小Q值中减去**熵项(α * log π(a'|s'))以获得"软目标值"。TD目标(y)由即时奖励和此软目标组合而成。主评论家网络(Q_ϕ，通常是双Q网络Q1, Q2)通过最小化与y之间的MSE损失**进行参数更新。

演员网络更新：演员网络**为批次状态s采样动作(a_π)。损失函数设计鼓励产生高Q值(由主评论家评估)且同时具有高熵(高log π)的动作分布**。损失函数近似为:

(α * log π − min(Q1, Q2)).mean()

Alpha自动调节(可选)：熵温度参数(α)可通过自动调节机制优化，方法是设定目标熵水平并调整α以促使**策略实际熵接近目标值**。

目标网络更新：目标评论家网络通过软更新机制逐步更新。SAC通常不使用目标演员网络，而是使用当前演员网络进行目标动作采样。

SAC的核心技术特点包括：

最大熵框架：将策略熵H(π(⋅∣s))_H_(_π_(⋅∣ _s_))作为奖励的补充项，在标准奖励基础上添加熵奖励。

随机演员设计：输出连续动作概率分布(如高斯分布)参数(均值、标准差)，并从中采样具体动作。

双Q网络机制：使用两个独立Q网络并取其目标值的最小值，以抑制Q值过估计问题(类似TD3)。

熵温度系数：控制奖励目标与熵目标间的平衡权重。可设为固定值或通过自动调整机制优化。

LOG_STD_MAX=2

LOG_STD_MIN=-20

EPSILON=1e-6# 用于log_prob计算中的数值稳定性

classActorNetworkSAC(nn.Module):

""" SAC的随机高斯演员。"""

def__init__(self, state_dim: int, action_dim: int, max_action: float):

super(ActorNetworkSAC, self).__init__()

self.layer1=nn.Linear(state_dim, 256)

self.layer2=nn.Linear(256, 256)

self.mean_layer=nn.Linear(256, action_dim) # 输出均值

self.log_std_layer=nn.Linear(256, action_dim) # 输出对数标准差

self.max_action=max_action

defforward(self, state: torch.Tensor) ->Tuple[torch.Tensor, torch.Tensor]:

""" 输出压缩后的动作及其对数概率。"""

x=F.relu(self.layer1(state))

x=F.relu(self.layer2(x))

mean=self.mean_layer(x)

log_std=self.log_std_layer(x)

log_std=torch.clamp(log_std, LOG_STD_MIN, LOG_STD_MAX) # 为稳定性而夹紧

std=torch.exp(log_std)

# 创建分布并使用重参数化技巧采样

normal_dist=Normal(mean, std)

z=normal_dist.rsample() # 可微分样本(压缩前)

action_squashed=torch.tanh(z) # 应用tanh压缩

# 计算log_prob并修正tanh

# log_prob = log_normal(z) - log(1 - tanh(z)^2 + eps)

log_prob=normal_dist.log_prob(z) -torch.log(1-action_squashed.pow(2) +EPSILON)

# 在动作维度上对log_prob求和(如果action_dim > 1)

log_prob=log_prob.sum(dim=-1, keepdim=True)

# 将动作缩放至环境边界

action_scaled=action_squashed*self.max_action

returnaction_scaled, log_prob

评论家网络采用类似于TD3的双Q网络架构，将状态和动作作为输入：

# SAC的评论家网络(双Q)

classCriticNetworkSAC(nn.Module):

def__init__(self, state_dim: int, action_dim: int):

super(CriticNetworkSAC, self).__init__()

# Q1架构

self.l1_q1=nn.Linear(state_dim+action_dim, 256)

self.l2_q1=nn.Linear(256, 256)

self.l3_q1=nn.Linear(256, 1)

# Q2架构

self.l1_q2=nn.Linear(state_dim+action_dim, 256)

self.l2_q2=nn.Linear(256, 256)

self.l3_q2=nn.Linear(256, 1)

defforward(self, state: torch.Tensor, action: torch.Tensor) ->Tuple[torch.Tensor, torch.Tensor]:

sa=torch.cat([state, action], 1)

q1=F.relu(self.l1_q1(sa))

q1=F.relu(self.l2_q1(q1))

q1=self.l3_q1(q1)

q2=F.relu(self.l1_q2(sa))

q2=F.relu(self.l2_q2(q2))

q2=self.l3_q2(q2)

returnq1, q2

SAC的更新逻辑结合了演员、评论家和可选的alpha参数优化。这些核心计算反映了SAC算法的关键特性，包括目标Q值计算中的熵项、演员损失中的熵正则化，以及双Q网络和可选的alpha自动调整机制。

学习算法

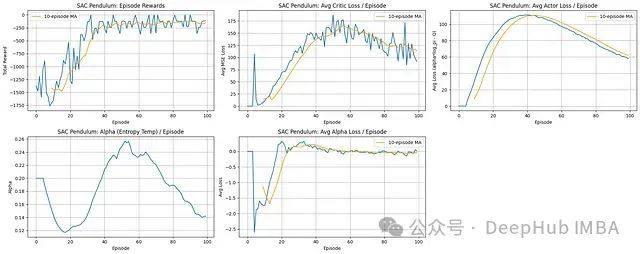
奖励曲线：SAC展示出优异的学习效率，累积奖励从初始约-1500迅速提升，并在大约40-50回合后稳定在约-200水平。收敛后的性能表现相对稳定，波动较小。

评论家学习：平均评论家损失在初期显著上升，随后在一定波动范围内趋于稳定，类似于DDPG的模式，反映了随着演员策略改进，评论家需要不断适应更高价值的状态-动作评估。

演员学习：演员损失曲线呈现先增后减的趋势，初期快速上升(表明策略成功更新朝向更高Q值方向)，在约40回合达到峰值，之后逐渐下降，这可能反映了策略稳定性提高和熵正则化效应的平衡。

熵温度调节：熵温度参数(Alpha)展示了动态调整过程，初期减小，在主要学习阶段(20-55回合)显著增加，随后再次降低，这与策略从初始探索逐渐转向利用阶段的预期行为一致。Alpha损失在零附近的波动确认了自动调整机制的有效运行，成功维持了目标熵水平。

SAC算法成功解决了钟摆控制任务，展现出较快的收敛速度和稳定的高奖励水平。熵温度参数(alpha)的自动调整机制在训练全过程中有效平衡了探索与利用的关系，促进了高效且稳健的学习过程。

12、TRPO (约束策略更新)

信任区域策略优化(TRPO)是一种创新的策略梯度算法，其核心目标是实现单调策略改进，通过约束机制确保(以高概率)每次策略更新不会导致性能下降。

该算法通过限制单次更新中策略变化幅度来实现学习稳定性，具体使用新旧策略间的KL散度作为变化度量标准。

TRPO属于在策略演员-评论家类算法(尽管评论家主要用于优势估计，不在核心TRPO约束更新机制内)。

算法的主要技术挑战在于如何高效求解其所涉及的约束优化问题。

学习算法

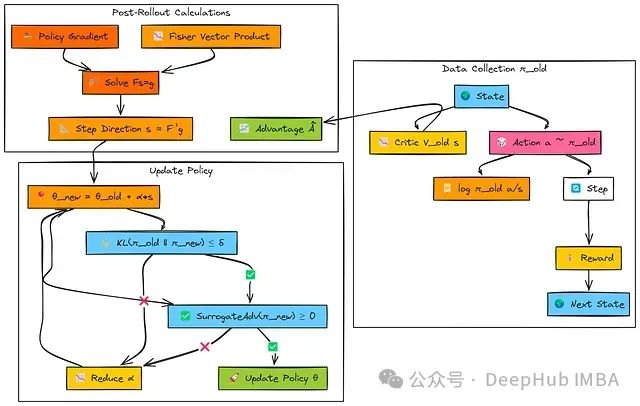
与其他在策略方法类似，TRPO使用当前策略(πold)收集经验批次并计算优势值(A)。随后计算标准策略梯度向量('g')。

TRPO的核心创新在于其更新步骤的计算方法。它不是简单地沿策略梯度'g'方向更新，而是求解一个约束优化问题：在保持新旧策略间KL散度低于阈值(δ)的前提下，最大化策略性能改进。

这一优化问题通过寻找满足Fs≈g的步骤方向's'来近似求解，其中F是Fisher信息矩阵(用于近似KL约束的曲率)。

TRPO采用共轭梯度(CG)算法高效计算's'，无需显式构建或求逆Fisher矩阵F。CG算法只需计算Fisher-向量积(FVP)。

确定更新方向后，通过回溯线搜索确定最大可行步长(α)，使得更新满足实际KL约束和替代目标改进条件。

学习算法

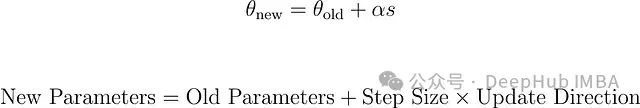
TRPO的关键技术要素包括：

信任区域约束：将策略更新限制在性能改进近似有效的区域内，确保学习过程的稳定性。

KL散度约束：使用平均Kullback-Leibler散度DKL(πold∣∣πnew)≤δ _DKL_ (_πold_ ∣∣ _πnew_ )≤ _δ_作为策略变化的度量标准。

Fisher信息矩阵(FIM)：表征策略分布空间的局部曲率特性。TRPO通过涉及FIM的二次形式来近似KL约束。

Fisher-向量积(FVP)： 一种利用自动微分高效计算FIM与任意向量乘积的技术，避免了构建和存储完整FIM的计算开销。

共轭梯度(CG)算法：一种迭代求解线性系统Fs≈g的方法，用于高效计算更新方向。

线搜索机制：确保最终采用的更新步长满足KL约束，并根据替代目标函数改进性能。

TRPO需要定义演员(策略网络)和评论家(价值网络)，结构与A2C/PPO等算法类似。

实现的复杂部分主要在于FVP计算、CG算法和线搜索机制。以下是概念性实现概述(详细完整实现请参考12_trpo.ipynb或a3c_training.py)：

# 使用Hessian-向量积近似计算Fisher向量积

# 这用于共轭梯度方法，计算TRPO更新步骤中的搜索方向

deffisher_vector_product(actor, states, vector, cg_damping):

log_probs=actor.get_log_probs(states).detach()

kl= (log_probs.exp() * (log_probs-log_probs.detach())).sum()

grads=torch.autograd.grad(kl, actor.parameters(), create_graph=True)

flat_grads=torch.cat([g.view(-1) forgingrads])

gv=torch.dot(flat_grads, vector)

hv=torch.autograd.grad(gv, actor.parameters())

flat_hv=torch.cat([h.view(-1) forhinhv])

# 添加阻尼项以提高数值稳定性

returnflat_hv+cg_damping*vector

# 实现共轭梯度方法解Ax = b

# 这用于近似TRPO更新步骤中的自然梯度方向

defconjugate_gradient(fvp_func, b, cg_iters=10, tol=1e-10):

x=torch.zeros_like(b) # 初始化解向量

r=b.clone() # 残差

p=b.clone() # 搜索方向

rs_old=torch.dot(r, r)

for_inrange(cg_iters):

Ap=fvp_func(p)

alpha=rs_old/torch.dot(p, Ap)

x+=alpha*p

r-=alpha*Ap

rs_new=torch.dot(r, r)

ifrs_new<tol:

break

p=r+ (rs_new/rs_old) *p

rs_old=rs_new

returnx

# 执行回溯线搜索以找到可接受的步长

# 确保满足KL散度约束

# 且新策略改进了替代损失

defbacktracking_line_search(actor, states, actions, advantages, old_log_probs,

step_direction, initial_step_size, max_kl, decay=0.8, max_iters=10):

theta_old= {name: param.clone() forname, paraminactor.named_parameters()} # 存储旧参数

foriinrange(max_iters):

step_size=initial_step_size* (decay**i) # 渐进减小步长

# 将步骤应用于演员参数

forparam, stepinzip(actor.parameters(), step_size*step_direction):

param.data.add_(step)

# 计算KL散度和替代损失

kl=actor.kl_divergence(states, old_log_probs)

surrogate=actor.surrogate_loss(states, actions, advantages, old_log_probs)

# 检查KL是否在约束内且替代损失是否有改善

ifkl<=max_klandsurrogate>=0:

returnstep_size*step_direction, True

# 如果步骤不成功，恢复旧参数

forname, paraminactor.named_parameters():

param.data.copy_(theta_old[name])

returnNone, False # 如果找不到有效步骤，返回失败

# 使用TRPO算法更新演员(策略)和评论家(价值函数)

defupdate_trpo(actor, critic, actor_optimizer, critic_optimizer,

states, actions, advantages, returns_to_go, log_probs_old,

max_kl=0.01, cg_iters=10, cg_damping=0.1, line_search_decay=0.8,

value_loss_coeff=0.5, entropy_coeff=0.01):

# 计算策略梯度

policy_loss=actor.surrogate_loss(states, actions, advantages, log_probs_old)

grads=torch.autograd.grad(policy_loss, actor.parameters())

g=torch.cat([grad.view(-1) forgradingrads])

# 使用共轭梯度计算自然梯度方向

fvp_func=lambdav: fisher_vector_product(actor, states, v, cg_damping)

step_direction=conjugate_gradient(fvp_func, g, cg_iters)

# 基于KL约束计算步长

sAs=torch.dot(step_direction, fvp_func(step_direction))

step_size=torch.sqrt(2*max_kl/ (sAs+1e-8))

# 执行回溯线搜索以确保满足KL约束

step, success=backtracking_line_search(actor, states, actions, advantages, log_probs_old,

step_direction, step_size, max_kl, line_search_decay)

# 如果成功，应用步骤

ifsuccess:

withtorch.no_grad():

forparam, step_valinzip(actor.parameters(), step):

param.data.add_(step_val)

# 计算并更新价值函数，使用MSE损失

value_loss=nn.MSELoss()(critic(states), returns_to_go)

critic_optimizer.zero_grad()

value_loss.backward()

critic_optimizer.step()

returnpolicy_loss.item(), value_loss.item() # 返回损失值，用于监控

TRPO通过利用Fisher信息矩阵(FIM)提供的二阶优化信息显式约束策略更新幅度，采用共轭梯度和Fisher-向量积技术高效实现计算，并通过线搜索确保每次更新的有效性。

学习算法

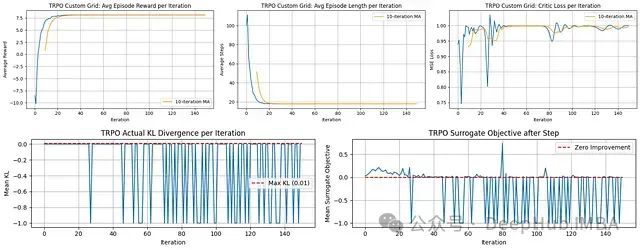
学习效率与性能：TRPO展示出极高的样本效率；平均奖励在仅约20-30次迭代内迅速攀升至接近最优水平，并保持稳定。平均回合长度同样呈现快速下降趋势，迅速稳定在较低水平。

评论家学习稳定性：评论家损失在初期波动后相对迅速地趋于稳定，表明价值函数学习过程高效且一致。

策略更新约束(KL散度)："实际KL散度"图显示每次迭代的策略变化量。TRPO设计目标是将这一变化量维持在较小范围内(低于红线所示Max KL阈值，通常约0.01)以确保更新稳定性。图中显示的值呈现异常(部分为负值，理论上KL散度不应为负)，但算法的设计意图是实现稳定、约束的更新。

优化目标进展："替代目标"图显示TRPO在采取更新步骤前计算的预期性能改进。曲线在零附近的波动表明逐步改进保证并非总是完美满足，但整体算法表现出色。

TRPO算法在网格任务上展示出卓越的样本效率，迅速收敛至高性能且稳定的策略。尽管内部优化指标(KL散度，替代目标)数据存在一定噪声或异常，但信任区域方法成功地引导学习过程快速达到有效解决方案。

13、DQN (深度Q学习)

Q-Learning算法在状态空间较小且结构清晰的环境中表现出色。然而，当面临非常大或连续的状态空间（例如处理游戏像素数据或机器人传感器输入）时，传统Q-Learning方法的有效性会显著降低。

深度Q网络(DQN)通过引入深度神经网络替代传统的Q表格，有效解决了这一问题。该网络参数化为Q(s,a;θ)，能够对Q值进行高效近似。

DQN引入了两项关键技术创新，用于稳定神经网络环境下的Q学习过程：经验回放(Experience Replay)和目标网络(Target Network)。

学习算法

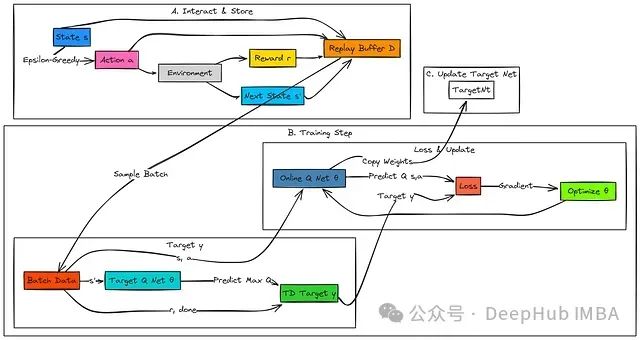
DQN的工作流程如下：

智能体基于主Q网络(Q_θ)采用epsilon-greedy策略与环境进行交互。每一个经验转换元组(s, a, r, s', done)被系统地存储在回放缓冲区(Replay Buffer)中。

在训练阶段，智能体从缓冲区中随机采样一个小批量(mini-batch)的历史经验。对于批次中的每个经验样本，系统计算目标Q值（即TD目标y），这一计算基于观察到的即时奖励r以及从后续状态s'可获得的最大Q值。后者通过一个参数更新频率较低的目标网络(Q_θ⁻)进行估计。

主Q网络负责预测在状态s下执行动作a的Q值。系统计算目标值y与预测Q值之间的误差（使用均方误差MSE或Huber损失函数），并通过梯度下降优化算法更新主Q网络的参数(θ)。

系统定期将主网络的权重参数复制到目标网络中：θ⁻ ← θ。

DQN的核心技术要素包括：

一个神经网络结构（如多层感知机MLP或卷积神经网络CNN），用于近似Q(s, a)函数。该网络通常接收状态s作为输入，输出所有可能离散动作的Q值。

一个用于存储历史交互数据(s, a, r, s', done)的经验缓冲区。通过采样随机小批量数据，有效打破了时序相关性，提高了学习过程的稳定性和效率。

Q网络的独立副本，其参数(θ⁻)更新频率较低（例如，每C步更新一次或通过慢速"软"更新机制）。这为学习过程提供了稳定的目标值：

学习算法

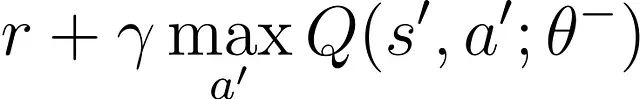
该方程为主Q网络训练提供了稳定的学习目标，有效防止了参数震荡。

首先，定义Q网络架构。对于简单的向量化状态表示（例如网格世界中的归一化坐标），多层感知机(MLP)结构通常已足够：

# DQN网络(MLP)

classDQN(nn.Module):

def__init__(self, n_observations: int, n_actions: int):

super(DQN, self).__init__()

self.layer1=nn.Linear(n_observations, 128)

self.layer2=nn.Linear(128, 128)

self.layer3=nn.Linear(128, n_actions) # 输出每个动作的Q值

defforward(self, x: torch.Tensor) ->torch.Tensor:

""" 前向传递获取Q值。"""

# 确保输入是正确设备上的浮点张量

ifnotisinstance(x, torch.Tensor):

x=torch.tensor(x, dtype=torch.float32, device=x.device)

elifx.dtype!=torch.float32:

x=x.to(dtype=torch.float32)

x=F.relu(self.layer1(x))

x=F.relu(self.layer2(x))

returnself.layer3(x) # 原始Q值

该网络结构学习从环境状态到动作价值的映射关系。

接下来，实现经验回放机制以存储交互经验：

# 用于存储转换的结构

Transition=namedtuple('Transition',

('state', 'action', 'next_state', 'reward', 'done'))

# 经验回放缓冲区

classReplayMemory:

def__init__(self, capacity: int):

self.memory=deque([], maxlen=capacity)

defpush(self, *args: Any) ->None:

""" 保存一个转换元组(s, a, s', r, done)。"""

# 确保张量存储在CPU上，避免GPU内存问题

processed_args= []

forarginargs:

ifisinstance(arg, torch.Tensor):

processed_args.append(arg.cpu())

elifisinstance(arg, bool): # 将done标志作为张量存储以保持一致性

processed_args.append(torch.tensor([arg], dtype=torch.bool))

else:

processed_args.append(arg)

self.memory.append(Transition(*processed_args))

•

• defsample(self, batch_size: int) ->Optional[List[Transition]]:

• """ 采样一个随机转换批次。"""

• iflen(self.memory) <batch_size:

• returnNone

• returnrandom.sample(self.memory, batch_size)

•

def__len__(self) ->int:

returnlen(self.memory)

此缓冲区设计允许从历史经验中采样不相关的批次数据进行训练更新。动作选择基于主Q网络的输出，采用epsilon-greedy策略：

# 动作选择(使用DQN的Epsilon-Greedy)

defselect_action_dqn(state: torch.Tensor,

policy_net: nn.Module,

epsilon: float,

n_actions: int,

device: torch.device) ->torch.Tensor:

""" 使用策略Q网络以epsilon-greedy方式选择动作。"""

ifrandom.random() <epsilon:

# 探索：选择一个随机动作

action=torch.tensor([[random.randrange(n_actions)]], device=device, dtype=torch.long)

else:

# 利用：根据Q网络选择最佳动作

withtorch.no_grad():

# 如果需要，添加批次维度，确保张量在正确设备上

state=state.unsqueeze(0) ifstate.dim() ==1elsestate

state=state.to(device)

# 获取Q值并选择具有最大Q的动作

action=policy_net(state).max(1)[1].view(1, 1)

returnaction

优化过程使用目标网络计算TD目标，并更新主策略网络参数：

# DQN优化步骤概述

defoptimize_model_dqn(memory: ReplayMemory,

policy_net: DQN,

target_net: DQN,

optimizer: optim.Optimizer,

batch_size: int,

gamma: float,

device: torch.device):

""" 对DQN策略网络执行一步优化。"""

# 1. 从内存中采样批次

# 2. 准备批次张量(states, actions, rewards, next_states, dones)在'device'上

# 3. 使用policy_net计算所采取动作的Q(s_t, a_t)

state_action_values=policy_net(state_batch).gather(1, action_batch)

# 4. 使用target_net计算V(s_{t+1}) = max_{a'} Q(s_{t+1}, a'; θ⁻)

withtorch.no_grad(): next_state_values=target_net(non_final_next_states).max(1)[0]

# 5. 计算TD目标y = reward + gamma * V(s_{t+1}) (处理终止状态)

expected_state_action_values= (next_state_values*gamma) +reward_batch

# 6. 计算Q(s_t, a_t)和TD目标y之间的损失(例如，Huber损失)

loss=F.smooth_l1_loss(state_action_values, expected_state_action_values.unsqueeze(1))

# 7. 优化policy_net

optimizer.zero_grad()

loss.backward()

torch.nn.utils.clip_grad_value_(policy_net.parameters(), 100) # 可选梯度裁剪

optimizer.step()

# 完整实现见13_dqn.ipynb

这一核心训练循环，结合目标网络的定期更新机制，使DQN能够在使用复杂函数近似器（如神经网络）的情况下实现有效学习。

学习算法

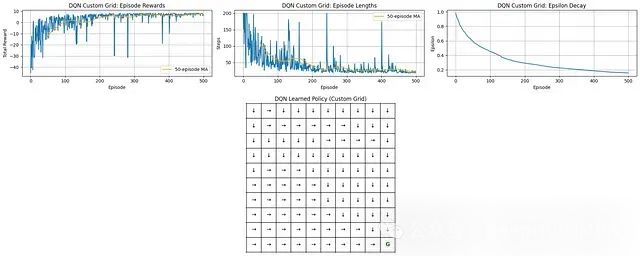
DQN实验结果分析：

学习进展：DQN展示了明显的学习效果。平均奖励值从初始的负值显著增长，在大约200-250回合后趋于稳定，达到持续性的正向奖励水平。

训练效率：回合长度随训练进程显著减少，与奖励增长趋势相一致，表明智能体逐步掌握了更高效地到达目标的能力。

探索机制：epsilon衰减曲线显示了探索行为的逐步减少过程，使智能体能够在后期训练阶段更有效地利用已习得的知识。

策略学习效果：最终学习得到的策略网格展示了一个结构合理的决策方案，动作选择通常引导智能体朝向目标状态'G'（位于网格右下角）。

DQN在自定义网格环境中成功学习了高效的导航策略，能够找到通向目标的最优路径。随着探索概率的逐步降低，性能指标（包括累积奖励和回合长度）显著改善并趋于稳定。

14、MADDPG (多智能体深度确定性策略梯度)

在多智能体学习环境中，当多个智能体同时进行学习时，会出现一个独特的技术挑战：环境非平稳性(Non-stationarity)。

从任何单个智能体的视角来看，随着其他智能体不断更新各自的策略，环境本身也在持续变化。多智能体深度确定性策略梯度(MADDPG)算法通过集中式训练、分散式执行(Centralized Training with Decentralized Execution)架构扩展了DDPG算法，有效解决了这一问题。

每个智能体基于其局部观察学习独立的Actor网络，但训练过程中每个智能体都拥有一个集中式Critic网络，该网络接收来自所有智能体的信息（包括观察和动作）。

这种训练阶段的信息共享机制有助于稳定整个学习过程。

学习算法

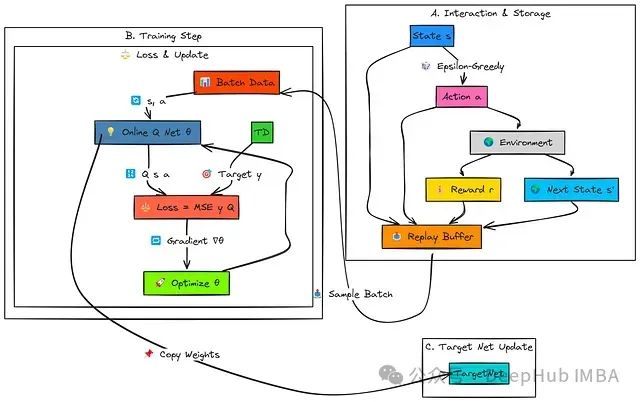
MADDPG工作流程：

每个智能体(1, 2, ...N)仅使用自身局部观察(o1, o2)和对应的Actor网络(μ_θ1, μ_θ2)在环境中生成动作(a1, a2)，并添加噪声以促进探索。系统将联合经验（包含所有观察、动作、奖励、后续观察）存储在共享回放缓冲区中。

Critic更新(智能体i)：智能体i的Critic网络(Q_ϕi)基于目标值进行参数更新。该目标值计算依赖于：智能体i的即时奖励(r_i)；目标集中式Critic(Q_ϕi′)的输出，该Critic接收以下输入：联合后续观察状态以及所有目标Actor网络(μ_θj′(o_j′))预测的后续动作

智能体i的Actor网络(μ_θi)参数更新目标是生成能够最大化其主集中式Critic(Q_ϕi)估计的Q值的动作，同时考虑所有Actor网络当前预测的动作分布。

所有目标网络通过从对应主网络进行缓慢的软更新来更新参数。

MADDPG的核心技术概念包括：

分散式Actor架构：每个智能体i拥有独立的策略网络μ_i(o_i)，该网络仅使用智能体局部观察o_i来选择动作a_i。

集中式Critic架构：每个智能体i配备对应的Critic网络Q_i(x, a_1, ..., a_N)，该网络以联合状态/观察x和所有智能体的动作(a_1, ..., a_N)作为输入，用于估计智能体i的价值函数。

离策略学习：算法使用存储联合交互数据的回放缓冲区，支持从历史经验中进行高效学习。

每个智能体的Actor网络设计通常类似于DDPG中的actor结构，输出确定性动作（如需处理离散动作空间，则可调整为输出动作概率分布）：

# Actor网络(类似于DDPG的，每个智能体一个)

classActorNetworkMADDPG(nn.Module):

def__init__(self, obs_dim: int, action_dim: int, max_action: float):

super(ActorNetworkMADDPG, self).__init__()

self.layer1=nn.Linear(obs_dim, 128)

self.layer2=nn.Linear(128, 128)

self.layer3=nn.Linear(128, action_dim)

self.max_action=max_action

defforward(self, obs: torch.Tensor) ->torch.Tensor:

x=F.relu(self.layer1(obs))

x=F.relu(self.layer2(x))

action=self.max_action*torch.tanh(self.layer3(x)) # 缩放的连续动作

returnaction

MADDPG与DDPG的关键区别在于集中式Critic设计，该Critic将全局信息作为输入：

# 集中式Critic网络(每个智能体一个)

classCentralizedCriticMADDPG(nn.Module):

def__init__(self, joint_obs_dim: int, joint_action_dim: int):

super(CentralizedCriticMADDPG, self).__init__()

# 输入大小 = 所有观察的组合维度 + 所有动作

self.layer1=nn.Linear(joint_obs_dim+joint_action_dim, 256)

self.layer2=nn.Linear(256, 256)

self.layer3=nn.Linear(256, 1) # 输出该智能体的单一Q值

defforward(self, joint_obs: torch.Tensor, joint_actions: torch.Tensor) ->torch.Tensor:

# 连接所有观察和所有动作

x=torch.cat([joint_obs, joint_actions], dim=1)

x=F.relu(self.layer1(x))

x=F.relu(self.layer2(x))

q_value=self.layer3(x)

returnq_value

该Critic网络设计用于学习特定智能体的期望回报，同时考虑环境中所有智能体的观察和行为。

回放缓冲区需要存储完整的联合经验数据(o_list, a_list, r_list, o_next_list, done_list)：

# --- MADDPG更新逻辑概述(对于智能体i) ---

# 假设已处理优化器、目标网络、批次采样

# 1. 从缓冲区中采样联合转换批次：

batch_obs, batch_actions, batch_rewards, batch_next_obs, batch_dones

# --- Critic_i更新 ---

with torch.no_grad():

target_next_actions = [target_actor_j(batch_next_obs_j) for j in range(num_agents)]

target_next_actions_cat = torch.cat(target_next_actions, dim=1)

joint_next_obs_cat = batch_next_obs.view(batch_size, -1)

q_target_next = target_critic_i(joint_next_obs_cat, target_next_actions_cat)

td_target_i = batch_rewards_i + gamma * (1 - batch_dones_i) * q_target_next

joint_obs_cat = batch_obs.view(batch_size, -1)

joint_actions_cat = batch_actions.view(batch_size, -1)

q_current_i = critic_i(joint_obs_cat, joint_actions_cat)

critic_loss_i = F.mse_loss(q_current_i, td_target_i.detach())

# 优化critic_i

# --- Actor_i更新 ---

# 冻结critic梯度

current_actions = [actor_j(batch_obs_j) for j in range(num_agents)]

current_actions[i] = actor_i(batch_obs_i)

current_actions_cat = torch.cat(current_actions, dim=1)

actor_loss_i = -critic_i(joint_obs_cat, current_actions_cat).mean()

# 优化actor_i

# 解冻critic梯度

# --- 软更新目标网络 ---

soft_update(target_critic_i, critic_i, tau)

soft_update(target_actor_i, actor_i, tau)

更新算法涉及上述组件的协同工作。通过在训练阶段使用集中式Critic架构，MADDPG为每个Actor提供了一个能够考虑其他智能体行为的稳定学习信号，有效缓解了非平稳性问题，同时保持了分散式执行的灵活性。

学习算法

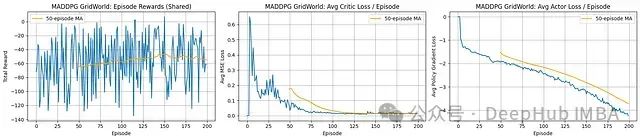
MADDPG实验结果分析：

奖励表现(共享)：每回合总共享奖励呈现显著波动，其移动平均线仅显示微弱的上升趋势，最终在一个相对较低的水平（约-50）趋于平稳。这表明智能体在学习过程中取得一定进展，但在200回合的训练周期内未能收敛至高效的合作策略。

Critic网络表现：平均Critic损失值快速下降并稳定在较低水平，表明Critic网络在预测当前智能体策略组合下的价值函数方面逐渐变得准确。

Actor网络表现：平均Actor损失（策略梯度）持续减小（朝负方向增大），表明Actor网络从对应Critic接收到一致的优化信号，策略更新方向符合预期。

MADDPG算法展示出明确的学习迹象，Critic和Actor损失均呈现一致的优化趋势。

然而，实际共享奖励的改善幅度有限且波动较大，未能展示强烈的收敛特征。

这种表现差异可能反映了多智能体协调学习的固有挑战、环境非平稳性的影响，或者表明需要更长的训练周期才能形成有效的协作策略。

15、QMIX (协作型价值分解方法)

QMIX(Q值混合)算法专为具有共享团队奖励的协作型多智能体强化学习任务设计。与MADDPG类似，它采用集中训练、分散执行的架构范式。

然而，QMIX的核心差异在于：它不是为每个智能体学习独立的集中式Critic，而是学习基于局部观察的个体智能体Q函数(Q_i)，并通过一个特殊设计的混合网络(Mixing Network)将它们组合，以估计联合行动价值函数(Q_tot)。

算法的关键技术洞见是：对于许多协作任务，如果一个智能体的行为增加了其局部效用(Q_i)，那么这一行为也应该增加（或至少不减少）整个团队的整体效用(Q_tot)。QMIX通过在混合网络内部结构中强制执行单调性约束(Monotonicity Constraint)来实现这一特性。

这一设计确保了基于个体Q_i值的分散贪婪动作选择与基于Q_tot选择的贪婪联合动作保持一致。

混合网络本身通过超网络(Hypernetworks)技术接收全局状态信息，使个体效用组合方式能够根据整体环境上下文动态调整。

学习算法

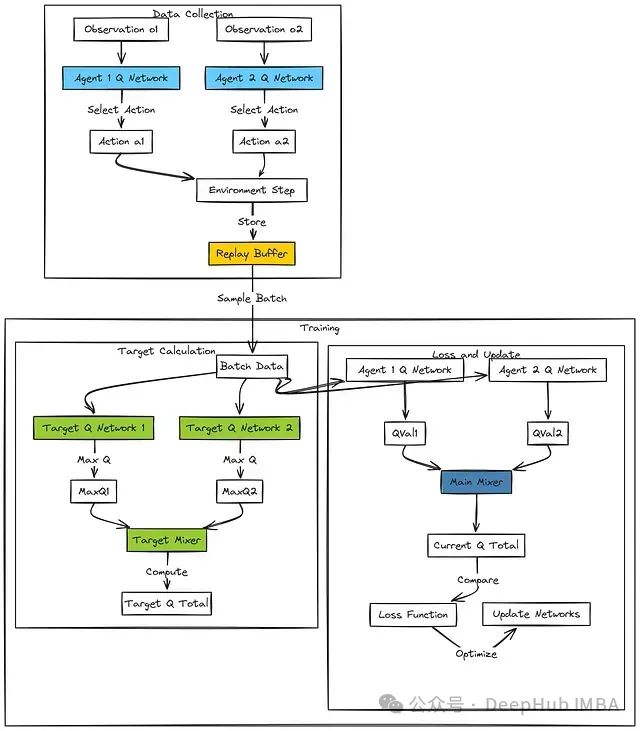
QMIX工作流程：

在执行阶段，每个智能体i基于其局部观察o_i和对应的网络Q_i(θ_i)选择动作a_i（通常采用epsilon-greedy策略）。系统存储包含全局状态x在内的完整联合交互经验。

目标Q_tot'计算过程：

对于每个智能体i，目标网络Q_i'(θ_i')用于确定从后续观察o_i'出发的最优动作对应的Q值。

这些个体最大Q值被输入到目标混合网络``f_mix'(ϕ_mix')中，该网络同时接收后续全局状态x'作为输入，综合生成目标联合价值Q_tot'。

系统计算标准TD目标y：y = r + γQ_tot'。

当前Q_tot计算与损失计算：

对于每个智能体i，主网络Q_i(θ_i)计算在当前批次数据中实际执行的动作a_i对应的Q值。

这些Q值与当前全局状态x一起输入到主混合网络``f_mix(ϕ_mix)中，生成当前联合价值估计Q_tot。

系统计算y与Q_tot之间的均方误差损失。

参数优化过程：

一个统一的优化器根据计算得到的损失函数值同时更新所有智能体网络(θ_i)和混合网络(ϕ_mix)的参数。各目标网络通过软更新机制定期更新参数。

首先，定义个体智能体网络结构。这是一个标准的Q网络设计，接收局部观察数据并输出每个可能动作的Q值：

# 智能体网络(类似于DQN的Q网络)

classAgentQNetwork(nn.Module):

def__init__(self, obs_dim: int, action_dim: int):

super(AgentQNetwork, self).__init__()

# 可以是MLP或RNN(DRQN)，取决于可观察性需求

self.fc1=nn.Linear(obs_dim, 64)

self.fc2=nn.Linear(64, 64)

self.fc3=nn.Linear(64, action_dim) # 每个动作的Q值

defforward(self, obs: torch.Tensor) ->torch.Tensor:

x=F.relu(self.fc1(obs))

x=F.relu(self.fc2(x))

q_values=self.fc3(x)

returnq_values

混合网络设计是QMIX的创新核心，它利用超网络技术实现单调性约束：

# 简化的QMIX混合网络

classQMixer(nn.Module):

def__init__(self, num_agents: int, global_state_dim: int, mixing_embed_dim: int=32):

super(QMixer, self).__init__()

self.num_agents=num_agents

self.state_dim=global_state_dim

self.embed_dim=mixing_embed_dim

# W1的超网络(生成正权重)

self.hyper_w1=nn.Sequential(

nn.Linear(self.state_dim, 64), nn.ReLU(),

nn.Linear(64, self.num_agents*self.embed_dim)

)

# b1的超网络

self.hyper_b1=nn.Linear(self.state_dim, self.embed_dim)

# W2的超网络(生成正权重)

self.hyper_w2=nn.Sequential(

nn.Linear(self.state_dim, 64), nn.ReLU(),

nn.Linear(64, self.embed_dim) # 输出大小embed_dim -> 重塑为(embed_dim, 1)

)

# b2的超网络(标量偏置)

self.hyper_b2=nn.Sequential(

nn.Linear(self.state_dim, 32), nn.ReLU(), nn.Linear(32, 1)

)

defforward(self, agent_qs: torch.Tensor, global_state: torch.Tensor) ->torch.Tensor:

# agent_qs形状：(batch_size, num_agents)

# global_state形状：(batch_size, global_state_dim)

batch_size=agent_qs.size(0)

agent_qs_reshaped=agent_qs.view(batch_size, 1, self.num_agents)

# 从全局状态生成权重/偏置

w1=torch.abs(self.hyper_w1(global_state)).view(batch_size, self.num_agents, self.embed_dim)

b1=self.hyper_b1(global_state).view(batch_size, 1, self.embed_dim)

w2=torch.abs(self.hyper_w2(global_state)).view(batch_size, self.embed_dim, 1)

b2=self.hyper_b2(global_state).view(batch_size, 1, 1)

# 混合层(确保第一层后有非线性如ELU/ReLU)

hidden=F.elu(torch.bmm(agent_qs_reshaped, w1) +b1) # (batch, 1, embed_dim)

q_tot=torch.bmm(hidden, w2) +b2# (batch, 1, 1)

returnq_tot.view(batch_size, 1) # 返回形状(batch, 1)

更新逻辑包括获取相关动作的Q_i值，将它们传入混合器，使用目标网络计算TD目标值，并通过混合网络和所有智能体网络反向传播损失梯度。

QMIX提供了一种结构化方法来学习协作策略，通过分解团队价值函数，同时确保个体行为贡献通过单调性约束与全局目标保持一致性。

学习算法

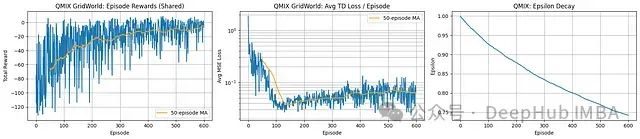
QMIX实验结果分析：

奖励表现(共享)：智能体展示了显著的学习进步。共享奖励曲线呈现明显的上升趋势，特别是在移动平均线中表现突出，从初始的显著负值增长至最终约-10至-20的水平。尽管性能有了实质性改善，但奖励仍然存在波动且未能稳定达到正值区间。

TD损失：平均TD损失（注意采用对数刻度）在前约150回合内急剧下降，幅度接近两个数量级，表明Q网络和混合器架构迅速学会了对联合动作价值进行有效近似。随后损失值在一个较低水平趋于稳定，表明系统成功学习到了相对于当前策略的准确值函数表示。

探索行为：Epsilon参数在整个训练过程中保持稳定但缓慢的衰减趋势。这种设计确保了持续的环境探索能力，可能导致奖励指标的持续性波动，但同时允许智能体有效逃离局部最优解。

QMIX算法成功促进了协作学习过程，导致共享奖励指标的显著改善。值函数学习（通过TD损失反映）表现出高效性并迅速达到稳定状态。尽管在训练后期奖励趋于平稳但仍有波动，总体趋势清晰展示了多智能体协作策略学习的成功进展。

16、HAC：层次化结构解决长时域任务

在长序列动作任务或奖励稀疏的环境中，传统扁平结构的强化学习智能体通常面临显著的性能挑战。

层次化强化学习(Hierarchical Reinforcement Learning, HRL)通过在多个抽象层次上构建策略体系来解决这一问题。该方法使高层策略能够为低层设定子目标，从而将复杂任务分解为更易处理的子任务序列。层次化演员-评论家(Hierarchical Actor-Critic, HAC)算法正是基于这一原理，结合了目标条件策略和后见之明经验回放技术。

学习算法

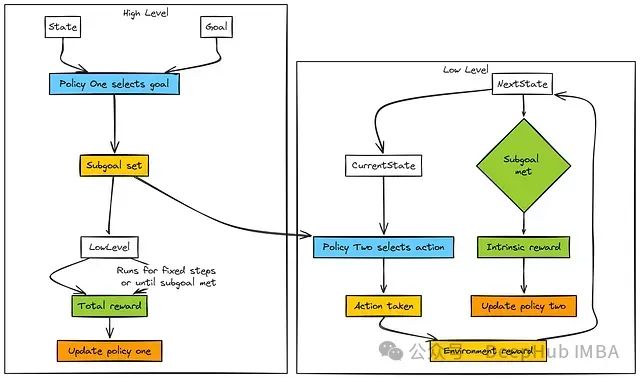
HAC (层次化演员-评论家)采用多层次结构：

高层(第1层)：接收当前状态 s 和最终目标 G 作为输入，其策略 (π_1) 为低层生成子目标 g₀。

低层(第0层)：接收当前状态 s 和来自高层的子目标 g₀，其策略 (π_0) 选择原始动作 a，旨在在固定时间范围 H 内实现子目标。低层根据子目标完成情况获得内在奖励，用于更新其策略参数。

高层更新机制：高层获取低层执行过程中累积的环境奖励总和，并基于状态转换(从设置子目标的初始状态到低层执行完毕的最终状态)来优化其策略。

两个层级均可利用评论家网络 (V_0, V_1) 来估计状态或状态-目标组合的价值或优势函数。后见之明经验回放技术(使用实际达到的状态重新标记转换样本)对于提高学习效率至关重要，尤其是对低层策略的训练。

在实现方面，目标条件网络是HAC算法的核心组件。对于离散网格世界环境，我们可以基于DQN的Q网络架构进行调整，输入维度需扩展为state_dim + goal_dim以同时接收状态和目标信息。

# 目标条件Q网络 (可用于HAC中的Actor/Critic代理)

# 假设状态和目标作为输入连接在一起

classGoalConditionedQNetwork(nn.Module):

def__init__(self, input_dim: int, action_dim: int):

super(GoalConditionedQNetwork, self).__init__()

self.fc1=nn.Linear(input_dim, 128)

self.fc2=nn.Linear(128, 128)

# 输出取决于层次：

# L0: 原始动作的Q值

# L1: 选择离散子目标的Q值

self.fc3=nn.Linear(128, action_dim)

defforward(self, state_goal_concat: torch.Tensor) ->torch.Tensor:

x=F.relu(self.fc1(state_goal_concat))

x=F.relu(self.fc2(x))

q_values=self.fc3(x)

returnq_values

# --- 网络维度 ---

# state_dim = env.state_dim

# goal_dim = env.goal_dim # 如果目标是状态，通常与state_dim相同

# primitive_action_dim = env.action_dim

# subgoal_action_dim = env.rows * env.cols # 如果子目标是离散网格单元

# low_level_net = GoalConditionedQNetwork(state_dim + goal_dim, primitive_action_dim)

# high_level_net = GoalConditionedQNetwork(state_dim + goal_dim, subgoal_action_dim)

此网络架构同时处理当前状态和目标作为输入，输出特定层次对应的动作Q值(L0层输出原始动作的Q值，L1层输出子目标选择的Q值)。

后见之明回放缓冲区是另一个关键组件，用于存储转换样本并根据实际达到的状态进行目标重新标记：

# 简化的后见之明回放缓冲区概念

classHindsightReplayBuffer:

def__init__(self, capacity: int, hindsight_prob: float=0.8):

self.memory=deque([], maxlen=capacity)

self.hindsight_prob=hindsight_prob

defpush(self, state, action, reward, next_state, goal, done, level, achieved_goal):

# 存储完整的转换，包括预期目标和实际达到的目标

self.memory.append({

'state': state, 'action': action, 'reward': reward,

'next_state': next_state, 'goal': goal, 'done': done,

'level': level, 'achieved_goal': achieved_goal

})

defsample(self, batch_size: int, level: int):

# 1. 筛选缓冲区中正确'level'的转换

# 2. 从这些转换中采样一批

# 3. 对于批次中的每个转换:

# - 保留原始转换(state, action, reward, next_state, goal, done)

# - 以'hindsight_prob'的概率:

# - 创建一个*新的*后见之明转换:

# - 使用相同的state, action, next_state。

# - 用'achieved_goal'替换'goal'。

# - 根据next_state是否匹配*新的*后见之明目标重新计算'reward'

# (例如，如果匹配则为0，如果不匹配则为-1，用于L0内在奖励)。

# - 根据是否达到后见之明目标重新计算'done'。

# - 将此后见之明转换添加到正在准备的批次中。

# 4. 将最终批次(原始+后见之明)转换为张量。

HAC算法的核心理念是将这些组件以层次化方式整合：高层策略生成子目标，低层策略在指定时间窗口内尝试实现这些子目标，而两个层次都通过离策略学习方法(包括后见之明重标记)从经验中进行优化。

学习算法

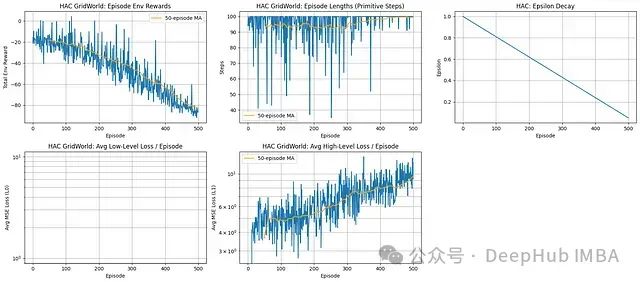
实验结果分析：

奖励表现：实验数据显示智能体表现出负向学习趋势，环境奖励在整个训练过程中持续下降。

执行效率：未观察到效率提升；回合长度持续维持在接近最大允许步数的水平。

层次化学习问题：高层损失函数呈现上升趋势，表明目标设定策略性能有所恶化。低层损失数据缺失或未显示，这进一步表明子目标实现层次也存在学习障碍。

探索策略：尽管实施了标准线性epsilon衰减探索机制，但未能有效解决基础学习问题。

基于以上分析，该HAC实现未能在网格世界任务环境中实现有效学习。关键性能指标显示，随时间推移，性能呈现下降趋势，表明在层次化学习框架实现中存在结构性问题。

17、MCTS：基于模拟的探索规划算法

蒙特卡洛树搜索(Monte Carlo Tree Search, MCTS)将强化学习的重点从学习覆盖整个状态空间的值函数或策略函数，转变为针对当前状态的在线规划方法。

给定特定状态，MCTS利用环境模型(或模拟器)生成大量可能的未来轨迹，构建搜索树以确定当前最有前景的动作选择。

学习算法

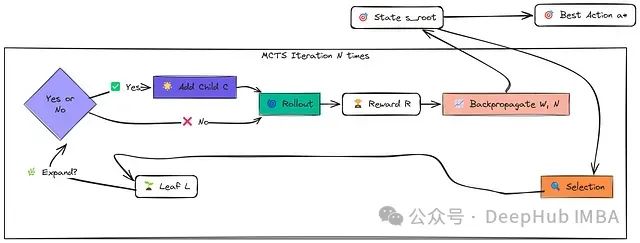
MCTS算法的每次迭代包含四个关键步骤，从当前状态对应的根节点开始：

选择(Selection)：根据选择策略(如UCB1)递归地选择子节点，从根节点遍历现有树结构。该策略平衡了探索(访问较少探索的节点)与利用(访问过去模拟中获得高平均奖励的节点)。此过程持续直到达到一个叶节点(尚未完全扩展的节点)。

扩展(Expansion)：若叶节点非终止节点，通过选择一个未尝试的动作并模拟执行，生成新状态，并将表示该新状态的节点添加到搜索树中。

模拟(Simulation/Rollout)：从新扩展节点(若无法扩展则为选择的叶节点)开始，使用简单、高效的"rollout策略"(通常为随机动作选择)进行模拟，直到回合结束或达到预设深度限制。记录此模拟过程获得的累积奖励。

反向传播(Backpropagation)：使用模拟获得的结果更新选择和扩展阶段访问过的所有节点的统计数据，包括访问计数和累积奖励值。

首先，我们需要定义树节点的数据结构：

classMCTSNode:

""" 表示蒙特卡洛树搜索中的节点。 """

def__init__(self, state: Tuple[int, int], parent: Optional['MCTSNode'] =None, action: Optional[int] =None):

self.state=state

self.parent=parent

self.action_that_led_here=action# 父节点采取的动作导致此节点

self.children: Dict[int, MCTSNode] = {} # 映射动作 -> 子节点

# 获取可能动作的函数(取决于环境)

self.untried_actions: List[int] =self._get_possible_actions(state)

self.visit_count: int=0

self.total_value: float=0.0# rollout奖励总和

def_get_possible_actions(self, state):

# 占位符：用实际环境调用替换

# 网格世界的示例(假设env可访问或已传递)：

ifenv.is_terminal(state): return []

returnlist(range(env.get_action_space_size())) # 或env.get_valid_actions(state)

defis_fully_expanded(self) ->bool:

returnnotself.untried_actions

defis_terminal(self) ->bool:

# 占位符：用实际环境调用替换

returnenv.is_terminal(self.state)

defget_average_value(self) ->float:

returnself.total_value/self.visit_countifself.visit_count>0else0.0

defselect_best_child_uct(self, exploration_constant: float) ->'MCTSNode':

""" 选择具有最高UCT评分的子节点。"""

best_score=-float('inf')

best_child=None

foraction, childinself.children.items():

ifchild.visit_count==0:

score=float('inf') # 优先选择未访问节点

else:

exploit=child.get_average_value()

explore=exploration_constant*math.sqrt(math.log(self.visit_count) /child.visit_count)

score=exploit+explore

ifscore>best_score:

best_score=score

best_child=child

ifbest_childisNone: # 只应在节点还没有子节点时发生

returnself# 理想情况下不应在没有子节点的节点上调用

returnbest_child

该节点类存储状态信息、父子节点关系链接以及关键的统计数据：访问计数(N)和累积价值(W)。

MCTS主搜索函数协调四个核心步骤(选择、扩展、模拟、反向传播)，从当前状态开始执行大量模拟，构建搜索树并利用积累的统计数据指导探索过程，最终确定最优即时动作。

学习算法

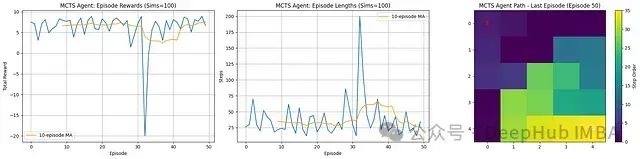
实验结果分析：

性能表现：MCTS算法持续实现正向总奖励，移动平均值稳定维持在+6至+7区间。这表明在给定的模拟预算(100次模拟)条件下，规划过程能有效找到高奖励路径。

执行效率：回合长度普遍较低且相对稳定，平均约为30-40步。数据未显示明显的下降趋势，这表明MCTS从早期阶段就能够发现高效路径，而非通过多回合学习逐步提升效率。

规划特性：作为规划算法，MCTS的性能主要取决于每个回合内的搜索质量。结果显示搜索过程持续有效，但不呈现传统强化学习算法中参数更新带来的典型"学习曲线"特征。

路径可视化：最后一个回合的智能体轨迹展示了从起点('S')到目标('G')的清晰、有向路径，直观验证了规划成功。

综合评估，MCTS算法有效利用其规划能力(基于100次模拟的预算)，在网格世界环境中稳定地发现通往目标的高质量、相对高效的路径，从训练初期就能实现稳定的正向奖励。

18、PlaNet：潜在空间规划网络

PlaNet(Deep Planning Network)代表一种先进的基于模型的强化学习方法，特别适用于处理高维观察数据(如图像)的学习任务。

其核心创新在于不直接在复杂的观察空间中学习世界模型(动力学模型)，而是在学习得到的紧凑潜在空间中构建模型并执行规划，大幅提高了计算效率。

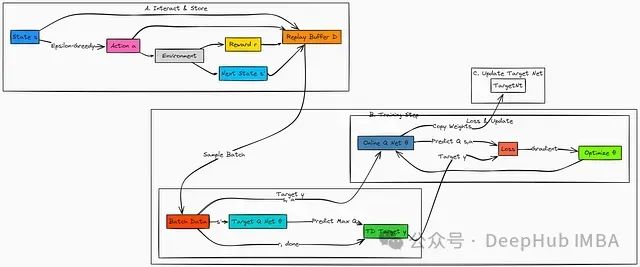
算法流程：智能体首先观察环境状态(o_t)，编码器将其(可能结合历史上下文)映射到潜在状态表示(s_t)。

规划器组件(通常采用交叉熵方法，CEM)利用当前潜在状态和习得的世界模型，在未来时域内搜索最优动作序列。

算法仅执行搜索得到的最优序列中的第一个动作(a_t*)，并将由此产生的观察(o_{t+1})、执行的动作(a_t*)、获得的奖励(r_t)及完成标志存储到回放缓冲区中。

同时，系统会从缓冲区中采样序列批次，用于训练和优化世界模型(包括编码器、转换预测器、奖励预测器等组件)。

实现一个完整的、支持图像处理和递归状态空间模型(RSSM)的PlaNet系统较为复杂。为简化说明，我们可以使用向量状态(如钟摆系统)的简化版本：

"潜在状态"可由环境的状态向量(或其简单MLP编码)近似表示

世界模型简化为预测下一状态向量和奖励的多层感知器(MLP)网络

# 简化的动力学模型(预测下一个状态向量和奖励)

classDynamicsModel(nn.Module):

def__init__(self, state_dim: int, action_dim: int, hidden_dim: int=200):

super(DynamicsModel, self).__init__()

self.fc1=nn.Linear(state_dim+action_dim, hidden_dim)

self.fc2=nn.Linear(hidden_dim, hidden_dim)

self.fc_next_state=nn.Linear(hidden_dim, state_dim)

self.fc_reward=nn.Linear(hidden_dim, 1)

defforward(self, state: torch.Tensor, action: torch.Tensor) ->Tuple[torch.Tensor, torch.Tensor]:

# 连接状态和动作

x=torch.cat([state, action], dim=-1)

x=F.relu(self.fc1(x))

x=F.relu(self.fc2(x))

pred_next_state=self.fc_next_state(x)

pred_reward=self.fc_reward(x)

returnpred_next_state, pred_reward

该网络学习基于当前状态和动作预测即时的状态转移和奖励。

规划器组件使用这个预测模型搜索最优动作序列。交叉熵方法(CEM)是PlaNet中常用的规划算法：

# CEM规划器概述

defcem_planner(model: DynamicsModel, initial_state: torch.Tensor, horizon: int,

num_candidates: int, num_elites: int, num_iterations: int,

gamma: float, action_low, action_high, action_dim, device) ->torch.Tensor:

# 初始化动作分布(例如，高斯mean=0, std=high)

action_mean=torch.zeros(horizon, action_dim, device=device)

action_std=torch.ones(horizon, action_dim, device=device) # 开始时方差高

for_inrange(num_iterations):

# 1. 采样候选动作序列(batch, horizon, action_dim)

action_dist=Normal(action_mean, action_std)

candidate_actions=action_dist.sample((num_candidates,))

candidate_actions=torch.clamp(candidate_actions, torch.tensor(action_low, device=device), torch.tensor(action_high, device=device))

# 2. 使用模型评估序列

total_rewards=torch.zeros(num_candidates, device=device)

current_states=initial_state.repeat(num_candidates, 1)

withtorch.no_grad():

fortinrange(horizon):

actions_t=candidate_actions[:, t, :]

next_states, rewards=model(current_states, actions_t)

total_rewards+= (gamma**t) *rewards.squeeze(-1) # 确保reward被挤压

current_states=next_states

# 3. 选择精英动作序列

_, elite_indices=torch.topk(total_rewards, num_elites)

elite_actions=candidate_actions[elite_indices]

# 4. 重新拟合动作分布

action_mean=elite_actions.mean(dim=0)

action_std=elite_actions.std(dim=0) +1e-6# 添加epsilon保持稳定性

# 返回最终平均序列的第一个动作

returnaction_mean[0]

CEM规划器通过迭代优化过程，使用学习的模型模拟多条轨迹，并将分布集中在高性能序列上，从而细化动作序列分布。

训练过程包括收集交互序列，将其存储在经验回放缓冲区中，并训练动力学模型以最小化预测误差(通常使用下一状态和奖励的均方误差损失)：

# --- 模型训练概述 ---

# (假设已定义model, optimizer, sequence_buffer)

for_inrange(num_train_steps):

1.从sequence_buffer中采样序列批次

2.对于序列中的每一步(或其子集):

-从批次获取state_t, action_t, reward_t, next_state_t

-预测next_state_pred, reward_pred=model(state_t, action_t)

-计算损失=MSE(next_state_pred, next_state_t) +MSE(reward_pred, reward_t)

3.平均批次/步骤的损失

4.optimizer.zero_grad()

5.loss.backward()

6.optimizer.step()

PlaNet算法展示了如何通过学习精确的世界模型，即使在压缩的潜在表示空间中，也能实现高效的规划，从而在复杂环境中实现高样本效率的学习。

学习算法

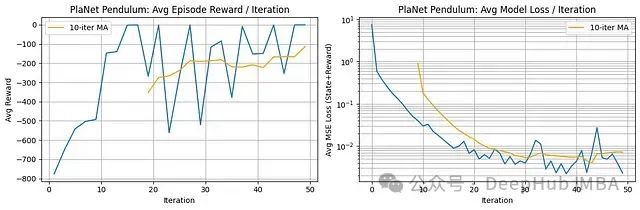
实验结果分析：

奖励表现：PlaNet展现出显著的学习进展。每回合平均奖励从极低的初始值(约-800)快速提升至较高水平(移动平均值达到约-100至-200)。然而，即使在初始快速改善后，迭代间的表现仍存在明显波动。

模型学习效果：平均模型损失(对数刻度)在初期阶段(前~25次迭代)大幅下降，降低了约两个数量级。随后损失在较低值处趋于稳定，表明PlaNet能够迅速学习钟摆系统动力学和奖励预测的准确模型。

基于模型的学习有效性：奖励的显著改善与模型损失的快速下降呈现强相关性。这凸显了PlaNet的核心优势：通过快速构建准确的世界模型，使其规划组件能够发现高奖励的动作策略。

综合评估，PlaNet在钟摆任务上展示了基于模型学习的显著效果。它能够迅速建立准确的世界动力学模型，从而使其规划机制能够实现显著的性能提升，尽管性能仍有一定波动性。

算法选择指南

针对不同任务场景的强化学习算法选择：

对于简单的离散动作任务，Q-Learning或SARSA算法是理想的起点。当任务要求更高的稳定性和样本效率时，尤其是在复杂环境中，近端策略优化(PPO)算法通常表现出较好的鲁棒性和学习效率。

对于机器人控制等连续动作空间问题，软演员-评论家(SAC)和深度确定性策略梯度(DDPG)算法是有力的选择，其中SAC通常在稳定性和探索效率方面表现更为出色。若环境模拟成本较低，基于模型的方法(如PlaNet)或基于规划的算法(如MCTS)可能会带来显著的性能优势。

尽管没有放之四海而皆准的算法选择，但PPO和SAC因其在多种现代强化学习任务中的良好表现而被广泛采用。建议从这些算法入手，并根据具体环境特性和任务目标进行适当调整。最优算法的选择最终取决于特定应用场景的具体需求和约束条件。

本文代码：

https://github.com/FareedKhan-dev/all-rl-algorithms

作者：Fareed Khan

打开APP阅读更多精彩内容