译码器的分类和应用

一、译码器的分类

译码器指的是具有译码功能的逻辑电路，译码是编码的逆过程，它能将二进制代码翻译成代表某一特定含义的信号（即电路的某种状态），以表示其原来的含义。译码器可以分为：变量译码和显示译码两类。

译码是编码的反过程，它是将代码的组合译成一个特定的输出信号。

分类：

（1）二进制译码器，又称为n-2n线译码器

将n种输入的组合译成2n种电路状态。也叫n---2n线译码器。

译码器的输入：一组二进制代码

译码器的输出：一组高低电平信号

（2）二－十进制译码器

直接输出二进制数，人们不太习惯，可采用二－十进制译码器来解决。

这种译码器有四个输入端，十个输出端。

（3）显示译码器

在数字测量仪表和各种数字系统中，都需要将数字量直观显示出来，一方面供人们直接读取测量和运算结果；另一方面用以监视数字系统的工作情况。

数字显示电路组成方块图如下所示。

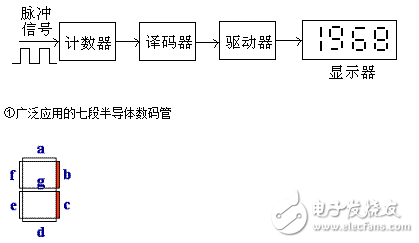
半导体数码管两种接法：

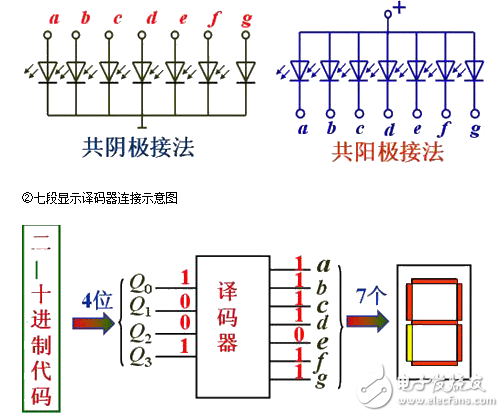
二、译码器的应用

三种基本译码器

在译码器基础中，解释了完全译码器（n-2n）的基本工作原理，即：当使能端有效时：

Yi = mi 或者

/Yi = ！mi （注：这里的！表示非号）

除了完全译码器之外，还有4-10线译码器，七段显示译码器，相对也比较简单，这里简单进行介绍：

- 4-10译码器

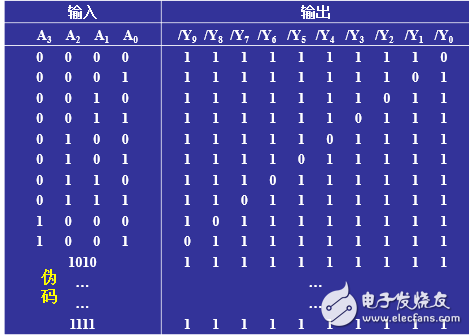
由真值表可以看出，当A3A2A1A0的取值为［0000~1001］时，输出有效，其它情况均为无效，其对应的逻辑器件图如下图所示：

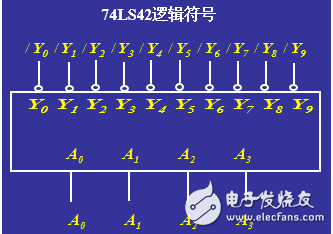
七段显示译码器

七段显示译码器一般用于液晶或LED显示屏，显示0~9数字（十进制）或0~F数字（十六进制）。所谓七段，表示的是0~9或0~F这些数字可用七根数码管显示，对应的图为：

对应的真值表如下图所示：

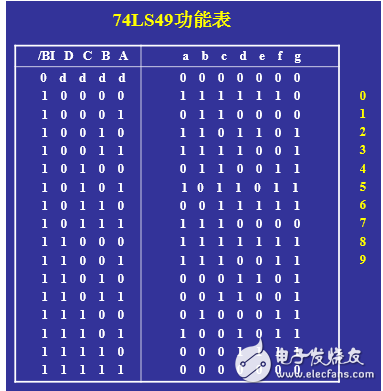
译码器的应用

译码器主要用于地址译码、指令译码以及逻辑表达式表示。下面重点解释如何内存寻址以及如何表达逻辑表达式。

内存寻址

在组合电路、时序电路在计算机课程中的地位一文中，说明了可执行程序的执行流程，其中的程序计数器（Program Counter，简称PC）中保存了CPU将要执行的指令，那如何在内存中定位到那条指令所在的内存地址呢？（重点理解：这是硬件实现，我们要用组合电路寻址）。

下图描述了早期8086的内存寻址方式。（计算机中用三类总线：数据总线、地址总线、控制总线进行数据传输，数据总线用于传输数据，地址总线用于传输地址，控制总线用于传输控制信号。三类总线用于在IO、内存、CPU以及外设之间进行数据传输；每一块内存中有rd、wr、adder、cs和data几个输入输出，其中的rd表示读内存，wr表示写内存，adder下文中解释，cs（chip select）表示片选，data用于内存和总线之间数据的传输）

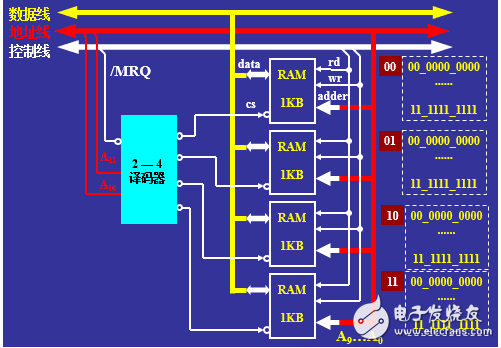
在8086机器中，内存只有4KB（受限于当时的生产工艺，4KB内存由4块1KB的内存块组成），用12位二进制串表示地址。对于每一块1KB的内存，其寻址范围为［00 0000 0000~11 1111 1111］，为了对4块内存都进行寻址，一般思路为：共享低10位（A9A8A7A6A5A4A3A2A1A0）的内存地址，高两位用A11A10来进行控制，使其满足：

- 当A11A10 = 00时选择第一块内存（从上向下看），此时A11A10A9A8A7A6A5A4A3A2A1A0表述的范围为［0000 0000 0000 ~ 0011 1111 1111］

- 当A11A10 = 01时选择第二块内存（从上向下看），此时A11A10A9A8A7A6A5A4A3A2A1A0表述的范围为［0100 0000 0000 ~ 0111 1111 1111］

- 当A10A10 = 01时选择第三块内存（从上向下看），此时A11A10A9A8A7A6A5A4A3A2A1A0表述的范围为［1000 0000 0000 ~ 1011 1111 1111］

- 当A11A10 = 11时选择第四块内存（从上向下看），此时A11A10A9A8A7A6A5A4A3A2A1A0表述的范围为［1100 0000 0000 ~ 1111 1111 1111］

显然，上面的地址真是我们需要表述的地址，剩下的就是如何用高两位A11A10来控制选择那一块1K的内存块。很自然的，2-4译码器正好能完成，因此，2-4译码器的输出分别接到每一块1k内存块上的片选信号，即可实现上述内存寻址功能。（adder用于合成A11A10和A9A8A7A6A5A4A3A2A1A0，使其构成一个12位地址）

译码器表达逻辑表达式

在译码器中，如果使能端有效，其对应的输入输出之间的关系为：

Yi = mi 或者

/Yi = ！mi （注：这里的！表示非号）

比较敏感的童鞋很容易发现，译码器和最小项存在关系。对于任何的逻辑表达式，都可以用最小项表示，如F（A，B，C）=m2+m3+m4+m5+m7。

根据/Yi = ！mi，可以进一步将F（A，B，C）表示成：

F（A，B，C） = ！（！m2 * ！m3 * ！m4 * ！m5* ！m7） （注：摩根定律）

F（A，B，C） = ！（/Y2*/Y3*/Y4*/Y5*/Y7）

此时，将3-8译码器的输出/Y2，/Y3，/Y4，/Y5和/Y7接入一个与非门，即可表示上面的逻辑表示式 F（A，B，C），其对应的电路图如下图所示：

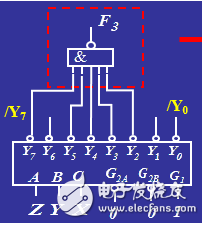
在上例的基础上，如何用74LS138译码器实现一个全减器呢？在设计之前，需要先明确减法器的功能，其真值如下图所示：

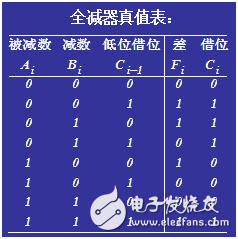
全减器中，Ci-1表示来自低位的借位，Ci表示向高位的借位，Fi表示本位的计算值。

根据真值表，很容易得到：

Fi = m1 + m2 + m4 + m7

Ci = m1 + m2 + m3 + m7

根据74LS138中的关系：/Yi = ！mi，得到：

Fi = ！/Y1 + ！/Y2 + ！/Y4 + ！/Y7 = ！（/Y1 * /Y2 * /Y4 * /Y7 ） （注：摩根定律）

Ci = ！/Y1 + ！/Y2 + ！/Y3 + ！/Y7 = ！（/Y1 * /Y2 * /Y3 * /Y7 ） （注：摩根定律）

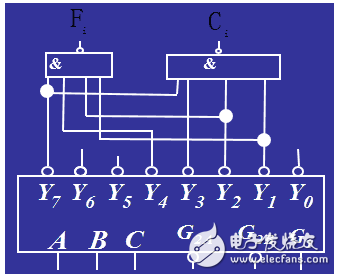
上述的Fi和Ci已经映射到74LS138的输出端口，将输出端口接入与非门，即可完成全减器，其对应的电路图如下图所示：