什么是码间串扰_码间串扰产生的原因是什么

　　什么是码间串扰

　　在一个抽样时刻，由于邻近码元的波形在该点的幅度值不为0，导致对当前码元抽样的干扰。也就是说，在抽样点得到的抽样值，不仅包含了当前码元的幅度值，还包含了临近码元的幅度值。

　　整体的波形是各个码元的波形相互叠加的结果，在没有码间干扰的情况下，不那么准确地说，就是不同码元的波形在时域上是没有重叠的，比方说在1s时刻到2s时刻之间是一个码元的波形，然后下一个码元的波形是从2s时刻之后开始，而码间干扰就是前一个码元的波形，延伸到了2s时刻之后。更准确地说法是，码间干扰是上一个码元的波形延伸到了第二个码元的抽样时刻，比方说2.5s时刻，从而对第二个码元的抽样判决造成了影响，前面的“没有重叠”这一条件就需要相应地改成是“在抽样时刻没有重叠”。

　　之所以我们只关注抽样时刻的情况，而不是严格地要求两个波形没有任何重叠，一方面是因为没有必要，在抽样时刻之外波形的重叠并不给抽样判决的结果带来影响，另一方面也是因为在实际情况下难以做到这一点。

　　

　　举例说明码间串扰

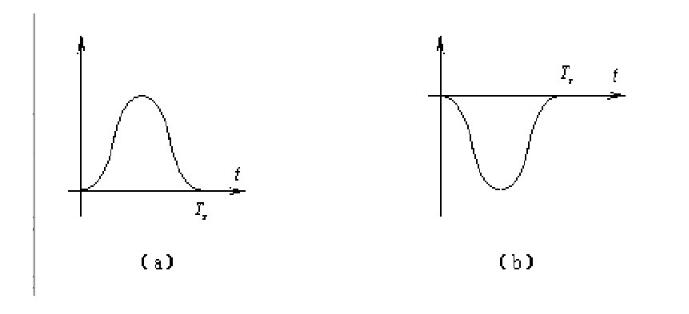
　　我们假定发端采用双极性码，当输入二进制码元序列中的“1”经过信道信号形成器后，输出一个正的升余弦波形，而当输入码时，“O”码时，则输出负的升余弦波形，分别如图（a）、（b）所示。

　　

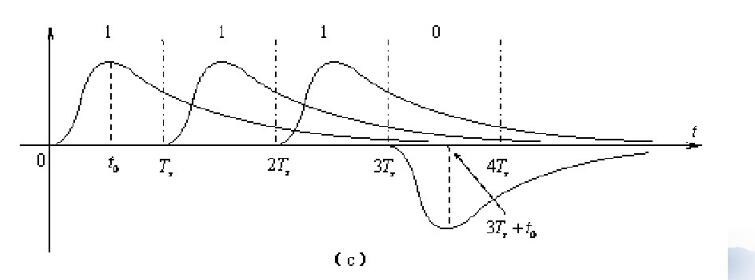
　　当输入的二进制码元序列为1110时，经过实际信道以后，信号将有延迟和失真，在不考虑噪声影响下，接收滤波器输出端得到的波形如图（c） 所示，第一个码元的最大值出现在tO时刻，而且波形拖得宽，这个时候对这个码元的抽样判决时刻应选择在t=t0时刻。依次类推，我们将在3T+t0时刻对第四个码元0进行判决。可从图中可以看到： 在t=3T+tO 时刻，第一码元、第二码元、第三码元等的值还没有消失，这样势必影响第四个码元的判决。即接收端接收到的前三个码元的波形串到第四个码元抽样判决的时刻，影响第四个码元的抽样判决。这种影响就叫做码间串扰。

　　

　　码间串扰产生的原因是什么

　　1、频带受限：这是在抽样判决之前，通过信道传输过来的信号需要经过一个滤波器，那么输入抽样判决器的信号，其频带宽度相比滤波之前的信号，频带受到了限制。

　　为什么频带受限会导致码间干扰呢？因为原始的波形在频域上本来是无限宽的——对于矩形脉冲信号而言，其傅里叶变换是抽样函数，布满了整个频域；经过滤波器之后，频域受限导致了波形在时域上的展宽，那么相邻的两个码元的波形，原本没有重叠的，现在由于“拖尾”的产生，上一个码元的波形就可能延伸到下一个码元的波形中去。

　　2、多径效应：这其实是考虑，同一码元波形的各个分量可能通过不同的路径传播，那么不同多径分量到达接收端的时间就不同，第一个多径分量到达的时刻和最后一个多径分量到达的时刻，这之间存在一个时间差，当这个时间差超过了一个码元的宽度之后，就意味着，上一个码元的一部分多径分量，在这个码元本应该传输完毕的时候，还没有到达接收点，而是混在了下一个码元的多径分量中到达的接收点，从而对下一个码元产生了干扰——叠加的时候不仅有自己的分量，还有别人的分量。

　　

　　消除码间串扰的基本思路

　　若想消除码间串扰，应使

　　

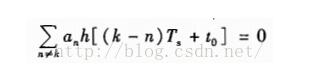
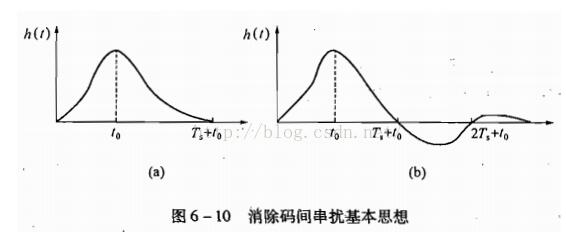
　　由于an是随机的，要想通过各项相互抵消使码间串扰为0是不行的，这就需要对h（t）的波形提出要求。如果相邻码元的前一个码元的波形到达后一个码元抽样判决时刻已经衰减到0，如图6-10（a）所示的波形，就能满足要求。但是，这样的波形不易实现，因为实际中的h（t）波形有很长的“拖尾”，也正是由于每个码元的“拖尾”造成了对相邻码元的串扰，但只要让它在Ts+t0、2Ts+t0等后面码元抽样判决时刻上正好为0，就能消除码间串扰，如图6-10（b）所示。这就是消除码间串扰的基本思想。

　　

　　码间串扰如何解决

　　1、选用抗干扰的码型。

　　2、优化电路。

　　3、注意EMI/EMC。