Amro通过一个简单的二元分类决策树解释信息熵和信息增益这两个概念

StackOverflow人气答主（top 0.12%）Amro通过一个简单的二元分类决策树例子，简明扼要地解释了信息熵和信息增益这两个概念。

为了解释熵这个概念，让我们想象一个分类男女名字的监督学习任务。给定一个名字列表，每个名字标记为m（男）或f（女），我们想要学习一个拟合数据的模型，该模型可以用来预测未见的新名字的性别。

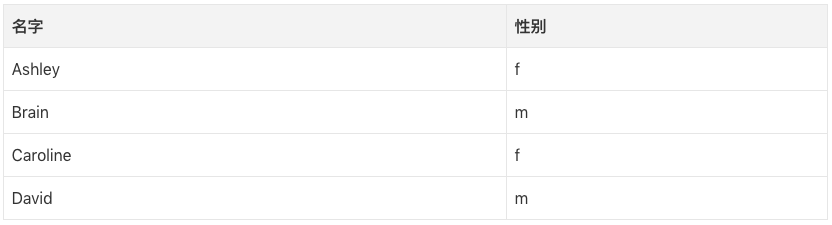
现在我们想要预测“Amro”的性别（Amro是我的名字）。

第一步，我们需要判定哪些数据特征和我们想要预测的目标分类相关。一些特征的例子包括：首/末字母、长度、元音数量、是否以元音结尾，等等。所以，提取特征之后，我们的数据是这样的：

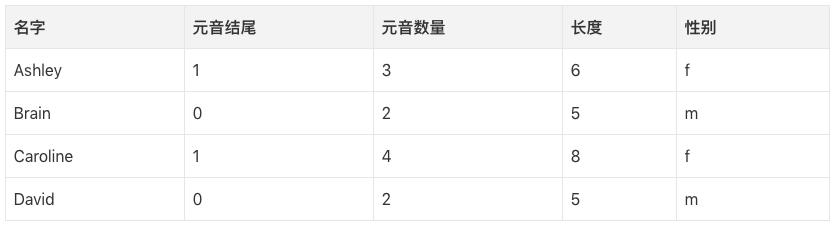
我们可以构建一棵决策树，一棵树的例子：

长度<7

|   元音数量<3: 男

|   元音数量>=3

|   |   元音结尾=1: 女

|   |   元音结尾=0: 男

长度>=7

|   长度=5: 男

基本上，每个节点代表在单一属性上进行的测试，我们根据测试的结果决定向左还是向右。我们持续沿着树走，直到我们到达包含分类预测的叶节点（m或f）。

因此，如果我们运行这棵决策树判定Amro，我们首次测试“长度<7？”答案为是，因此我们沿着分支往下，下一个测试是“元音数量<3？”答案同样为真。这将我们导向标签为m的叶节点，因此预测是男性（我碰巧是男性，因此这棵决策树的预测正确）。

决策树以自顶向下的方式创建，但问题在于如何选择分割每个节点的属性？答案是找到能将目标分类分割为尽可能纯粹的子节点的特征（即：只包含单一分类的纯粹节点优于同时包含男名和女名的混合节点）。

这一纯粹性的量度称为信息。它表示，给定到达节点的样本，指定一个新实例（名字）应该被分类为男性或女性的期望的信息量。我们根据节点处的男名分类和女名分类的数量计算它。

另一方面，熵是不纯粹性的量度（与信息相反）。对二元分类而言，熵的定义为：

Entropy = - p(a)*log(p(a)) - p(b)*log(p(b))

这一二元熵函数的图像如下图所示。当概率为p=1/2时，该函数达到其最大值，这意味着p(X=a)=0.5或类似的p(X=b)=0.5，即50%对50%的概率为a或b（不确定性最大）。当概率为p=1或p=0时（完全确定），熵函数达到其最小值零（p(X=a)=1或p(X=a)=0，后者意味着p(X=b)=1）。

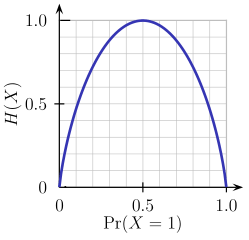
当然，熵的定义可以推广到有N个离散值（超过2）的随机变量X：

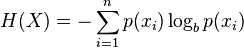
（公式中的log通常为以2为底的对数）

回到我们的名字分类任务中，让我们看一个例子。想象一下，在构建决策树的过程中的某一点，我们考虑如下分割：

以元音结尾

[9m,5f]

/          \

=1          =0

-------     -------

[3m,4f]     [6m,1f]

如你所见，在分割前，我们有9个男名、5个女名，即P(m)=9/14，P(f)=5/14。根据熵的定义，分割前的熵为：

Entropy_before = - (5/14)*log2(5/14) - (9/14)*log2(9/14) = 0.9403

接下来我们将其与分割后的熵比较。在以元音结尾为真=1的左分支中，我们有：

Entropy_left = - (3/7)*log2(3/7) - (4/7)*log2(4/7) = 0.9852

而在以元音结尾为假=0的右分支中，我们有：

Entropy_right = - (6/7)*log2(6/7) - (1/7)*log2(1/7) = 0.5917

我们以每个分支上的实例数量作为权重因子（7个实例向左，7个实例向右），得出分割后的最终权重：

Entropy_after = 7/14*Entropy_left + 7/14*Entropy_right = 0.7885

现在比较分割前后的权重，我们得到信息增益的这一量度，也就是说，基于特定特征进行分割后，我们获得了多少信息：

Information_Gain = Entropy_before - Entropy_after = 0.1518

你可以如此解释以上运算：通过以“元音结尾”特征进行分割，我们得以降低子树预测输出的不确定性，降幅为一个较小的数值0.1518（单位为比特，比特为信息单位）。

在树的每一个节点，为每个特征进行这一运算，以贪婪的方式选择可以取得最大信息增益的特征进行分割（从而偏好产生较低不确定性/熵的纯分割）。从根节点向下递归应用此过程，停止于包含的节点均属同一分类的叶节点（不用再进一步分割了）。

注意，我省略了超出本文范围的一些细节，包含如何处理数值特征、缺失特征、过拟合、剪枝树，等等。