一文读懂LC滤波器简单设计方法及原理介绍

　　LC滤波器概述

　　LC滤波器也称为无源滤波器，是传统的谐波补偿装置。LC滤波器之所以称为无源滤波器，顾名思义，就是该装置不需要额外提供电源。LC滤波器一般是由滤波电容器、电抗器和电阻器适当组合而成，与谐波源并联，除起滤波作用外，还兼顾无功补偿的需要。

　　LC滤波器是利用电感、电容和电阻的组合设计构成的滤波电路，可滤除某一次或多次谐波，最普通易于采用的无源滤波器结构是将电感与电容串联，可对主要次谐波（3、5、7）构成低阻抗旁路；单调谐滤波器、双调谐滤波器、高通滤波器都属于无源滤波器。

　　LC滤波器的分类

　　调谐滤波器

　　调谐滤波器包括单调谐滤波器和双调谐滤波器，可以滤除某一次（单调谐）或两次（双调谐）谐波，该谐波的频率称为调谐滤波器的谐振频率。

　　高通滤波器

　　高通滤波器也称为减幅滤波器，主要包括一阶高通滤波器、二阶高通滤波器、三阶高通滤波器和c型滤波器，用来大幅衰减低于某一频率的谐波，该频率称为高通滤波器的截止频率。

　　影像参数滤波器

　　以影像参数理论为基础设计实现的滤波器。这种滤波器是由若干个基本节（或半节）按联接处影像阻抗相等的原则级联组成的。基本节按电路结构分有定k型和m导出型。以LC低通滤波器为例，定k型低通基本节的阻带衰减随频率增加而单调增大；m导出型低通基本节则在阻带中某频率处有衰减峰，衰减峰的位置由m导出节中的m值控制。各低通基本节级联后构成的低通滤波器，固有衰减等于各基本节的固有衰减之和，当滤波器两端终接的电源内阻抗和负载阻抗分别等于其两端的影像阻抗时，该滤波器的工作衰减和相移就分别等于其固有衰减和相移。图1（a）所示的滤波器是由一个定k节和两个m导出节级联组成，Zπ和Zπm为影像阻抗。图1（b）为其衰减频率特性。阻带内两个衰减峰/f∞1和f∞2的位置分别由两个m导出节的m值决定。

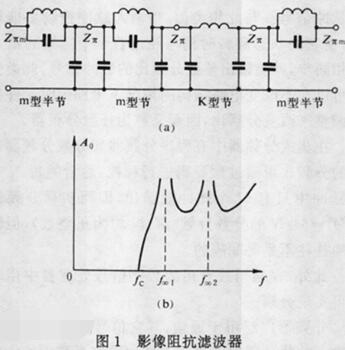
图一

　　同理，高通、带通和带阻滤波器也可用相应的基本节组成。

　　滤波器的影像阻抗不可能与纯电阻性的电源内阻以及负载阻抗在整个频带都相等（在阻带内相差更大），固有衰减与工作衰减在通带内有较大的差异。为了确保技术指标的实现，通常是在设计中预留足够的固有衰减裕度和增大通带宽度来弥补。

　　工作参数滤波器

　　这种滤波器不是由基本节级联组成和，而是用可以由R、L、C以及互感元件物理实现的网络函数去精确逼近滤波器的技术指标，然后由求得的网络函数实现相应的滤波器电路。根据不同的逼近准则，可以得出不同的网络函数，从而实现不同类型的滤波器。图2（a）是用最平幅度逼近（勃脱华兹逼近）实现的低通滤波器的特性；通带在零频附近最为平坦，趋向阻带时衰减单调增大。图2（c）是用等波纹逼近（切比雪夫逼近）实现的低通滤波器的特性；在通带内衰减在零和上限值之间做等幅起伏，在阻带内衰减单调增大。图2（e）是用椭圆函数逼近实现低通滤波器的特性，衰减在通带和阻带内都呈现等伏变化。图2（g）是用实现的低通滤波器的特性；在通带内衰减做等幅起伏，在阻带内衰减按指标要求的起落而做相应的起伏。图2（b）、（d）、（f）、（h）分别是这些低通滤波器相应的电路。

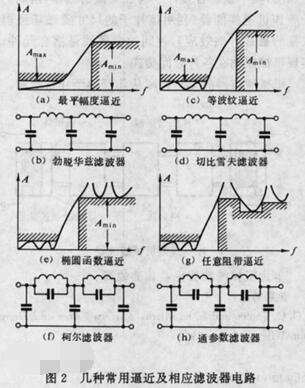
图2

　　高通、带通、带阻滤波器通常利用频率变换的方法由低通导出。

　　工作参数滤波器是由综合法精确地按技术指标要求设计出来的，能得出性能优良和经济的滤波器电路。

　　LC滤波器简单设计法

　　滤波器按照通带特性分类有：低通滤波器（LPF）、高通滤波器（HPF）、带通滤波器（BPF）、带阻滤波器（BRF）、全通滤波器（APF）。关于全通滤波器说明一下，从频率的选择上没有什么特别的作用，因为它基本不具备选频特性，那么这个滤波器有什么用呢？当信号通过这个滤波器时，不会损失任何频率成分，但是信号所包含的各频成分的延时会随频率不同而不同，那么这个滤波器的作用就是改变信号延时，常用在对系统延时进行补偿的场合，也成为移相器。

　　大家都知道理想的滤波器矩形窗是很难实现的，设计时使用某个函数逼近窗函数来进行设计，这样的滤波器设计方法称为函数型滤波器，根据函数对滤波器进行分类：

　　巴特沃斯型滤波器，在通带内响应最为平坦。

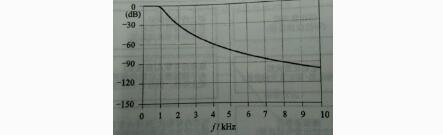
　　图1巴特沃斯型滤波器

　　切比雪夫型滤波器（等波纹滤波器），截止频率特别好，群延时特性不太好，通带内有等波纹起伏。

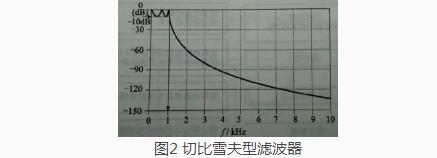
　　图2切比雪夫型滤波器

　　逆切比雪夫型滤波器（巴特沃斯-切比雪夫滤波器），阻带内有零点（陷波点），椭圆滤波器有更好的截止特性，因此并不经常使用。

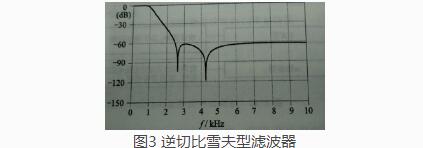
　　椭圆滤波器（联立切比雪夫滤波器），通带内有起伏，阻带内有零点（陷波点），截止频率比其他滤波器都好，但是对器件要求很高。

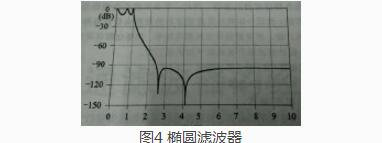
　　贝塞尔型滤波器（延时最平伏滤波器），通带内延时特性最为平坦，截止特性特别差。

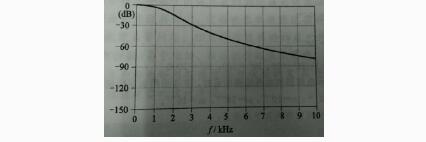
　　图5贝塞尔滤波器

　　一般没有特别要求可以选择巴特沃斯滤波器，衰减特性和相位特性都比较好。对衰减特性有要求的情况，可以选择切比雪夫滤波器，但是其相位特性不是很好，对非正弦信号会产生失真。对相位特性由要求的情侣，可以选择贝塞尔滤波器，输出信号一般不会失真。一般滤波器通带内有起伏，则衰减特性会比较好。

　　低通滤波器设计（LPF）

　　以上基于函数的滤波器设计都是现代模拟滤波器设计的典型方法，比较古典的基于映像参数的设计方法，在设计方法上比较简单，但是相较则截止频率不准确、性能较差。

　　定K型滤波器，以变量f作为截止频率，计算时只需要将f换成实际截止频率即可。

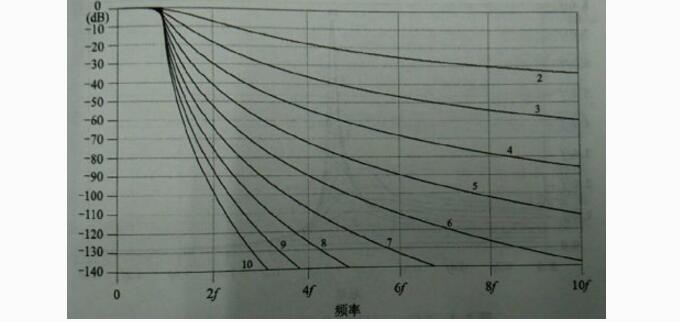
　　图62~10阶定K型LPF滤波器衰减特性

　　依据归一化LPF设计定K型滤波器

　　计算步骤：归一化低通滤波器——》截止频率变换——》特征阻抗变换

　　M=（待设计滤波器的截止频率）/（基准滤波器的截止频率）

　　K=（待设计滤波器的特征阻抗）/（基准滤波器的特征阻抗）

　　电感值计算：L‘=（L*K）/M

　　电容值计算：C’=C/（K*M）

　　例如：2阶定K型归一化LPF电路，截止频率为1/（2*pi）（pi代表数学圆周率），特征阻抗为1欧姆。

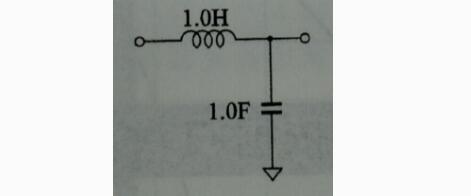
　　图7归一化2阶定K型LPF

　　设计截止频率为1KHz，特征阻抗为50欧姆的LPF定K型滤波器。

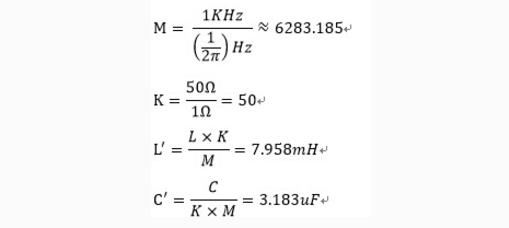
　　由此可以得到所设计的滤波器：

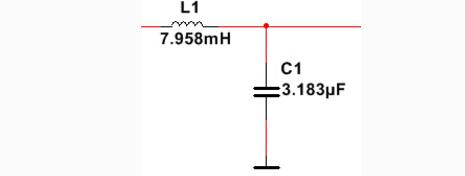
　　图8截止频率为1KHz，特征阻抗为50欧姆的定K型LPF

　　使用multisim对设计的滤波器进行仿真：

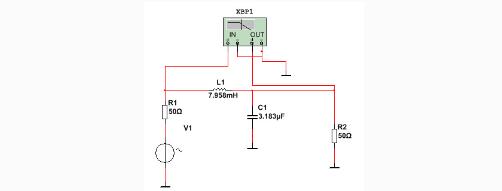
　　图9仿真电路

　　可以得到仿真幅频特性曲线：

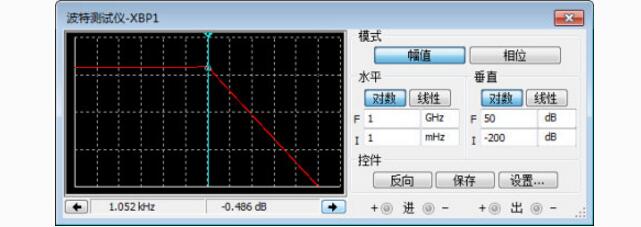
　　图10仿真幅频特性曲线结果

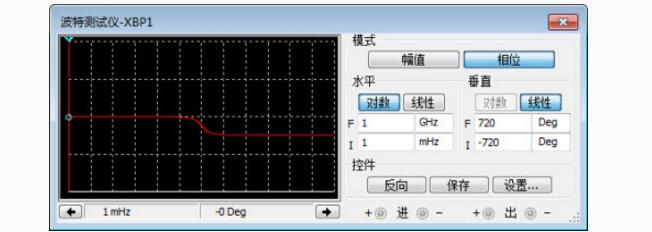
　　图11仿真相频特性曲线结果

　　用软件仿真结果还是可以的，对于实际电路就需要进行实际的测试了。

　　以上过程给大家一个计算方法，对于其他滤波器都可以使用相同的方法，一下提供给大家一些归一化的电路参数，大家在进行计算后先使用仿真软件进行一下仿真，结果有所偏差可以适当更换元件值，最后再实际电路上使用还需要进行实际调整。

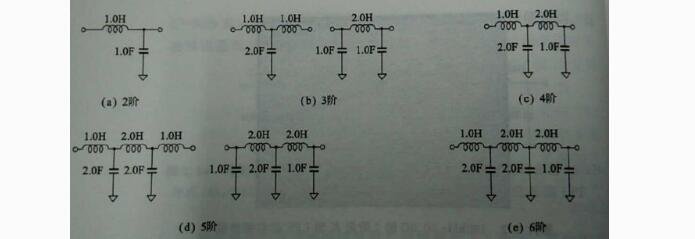
　　图12定K型LPF归一化电路参数（截止频率都为1/（2*pi），特征阻抗都为1欧姆）

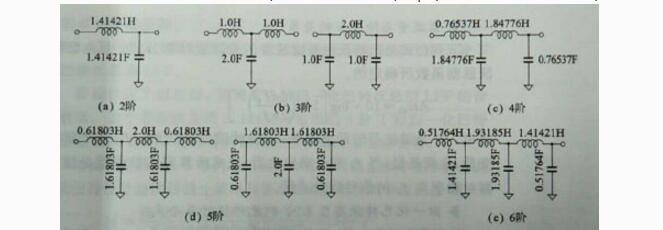
　　图13巴特沃斯LPF滤波器归一化电路参数（截止频率都为1/（2*pi），特征阻抗都为1欧姆）

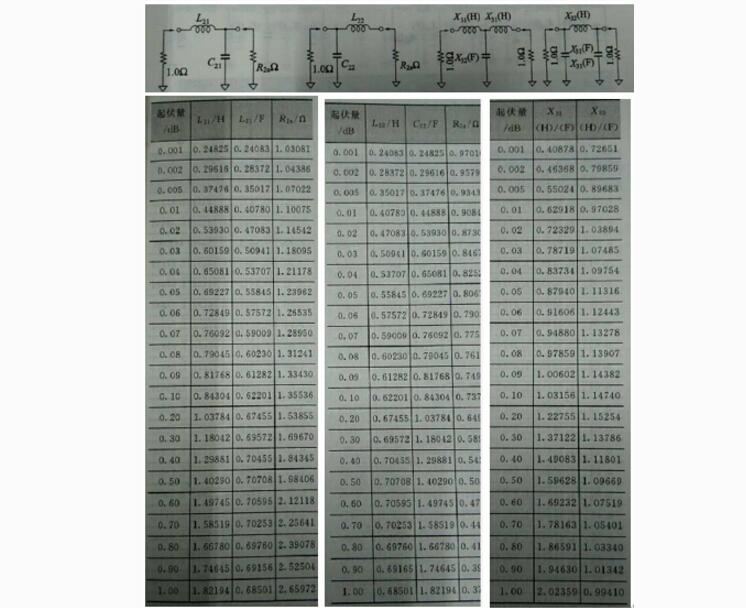
　　图14切比雪夫LPF归一化电路参数（截止频率都为1/（2*pi），特征阻抗都为1欧姆）

　　由于切比雪夫滤波器在通带内有起伏，因此多了一个起伏参数，在进行参数选择的时候需要注意与起伏量对应。

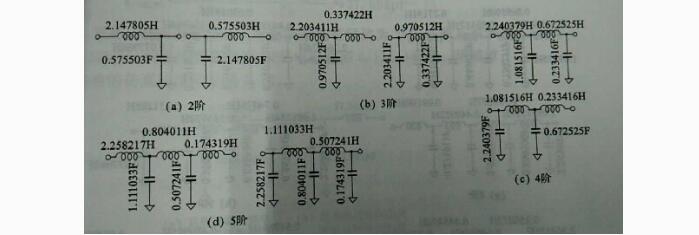
　　图15贝塞尔LPF归一化电路参数（截止频率都为1/（2*pi），特征阻抗都为1欧姆）

　　高通滤波器设计（HPF）

　　高通滤波器设计是以低通滤波器为基础进行的，从归一化LPF求取归一化HPF，此后则是按照上述步骤求解即可。从归一化LPF到归一化HPF的计算方法为：1、将电路中电容换成电感，电感换成电容；2、将原来的元件值取倒数，注意单位。以上两步即可得到归一化的HPF电路，如图16所示。

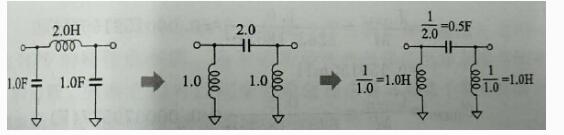
　　图16由归一化LPF转换为归一化HPF过程

　　之后的计算同上面进行LPF计算一样，求取M和K，然后计算L和C的值。

　　带通滤波器设计（BPF）

　　带通滤波器的设计也是通过低通滤波器设计过来的，具体设计步奏叫高通滤波器稍微多一点。

　　计算方法：

　　1、根据BPF的带宽和特征阻抗得到LPF的截止频率和特征阻抗，LPF的截止频率等于BPF的带宽

　　2、由之前讲到的LPF的设计方法，计算出满足条件的LPF滤波器电路

　　3、进行元件变换，需要使用到带通滤波器的中心频率，变换方法如下图所示：

　　图17电容元件的电路变换

　　元件值计算方法：

　　图18电感元件的电路变换

　　元件值计算方法：

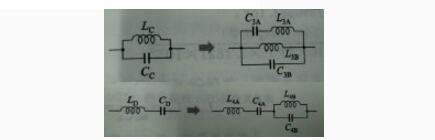
　　图19串并联电路的变换

　　略微复杂的电路，如图19所示，实际变换原理是一样的，都是将电容变换成电容与电感的并联，电感元件变成电感与电容的串联。

　　以上变换过程就是BPF设计的特别地方，方法也是比较简单的。

　　LC滤波器的原理图

　　LC滤波器之所以称为无源滤波器，顾名思义，就是该装置不需要额外提供电源。LC滤波器一般是由滤波电容器、电抗器和电阻器适当组合而成，与谐波源并联，除起滤波作用外，还兼顾无功补偿的需要。

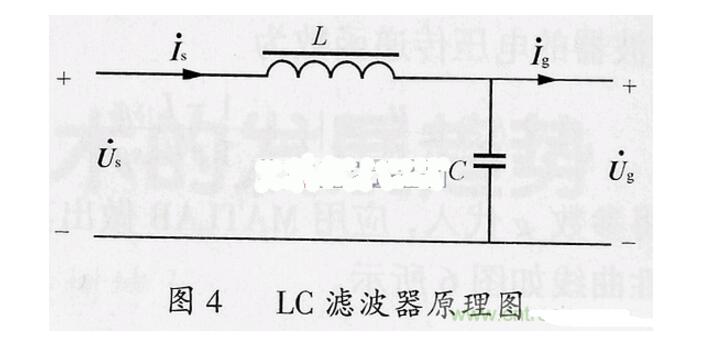
　　LC滤波器按照功能分为LC低通滤波器、LC带通滤波器、高通滤波器、LC全通滤波器、LC带阻滤波器；

　　按调谐又分为单调谐滤波器、双调谐滤波器及三调谐滤波器等几种。

　　LC滤波器设计流程主要考虑其谐振频率及电容器耐压，电抗器耐流。

　　在电子线路中，电感线圈对交流有限流作用，由电感的感抗公式XL=2πfL可知，电感L越大，频率f越高，感抗就越大。因此电感线圈有通低频，阻高频的作用，这就是电感的滤波原理

　　LC滤波电路一

　　电感在电路最常见的作用就是与电容一起，组成LC滤波电路。我们已经知道，电容具有“阻直流，通交流”的本领，而电感则有“通直流，阻交流，通低频，阻高频”的功能。如果把伴有许多干扰信号的直流电通过LC滤波电路（如图），那么，交流干扰信号大部分将被电感阻止吸收变成磁感和热能，剩下的大部分被电容旁路到地，这就可以抑制干扰信号的作用，在输出端就获得比较纯净的直流电流。

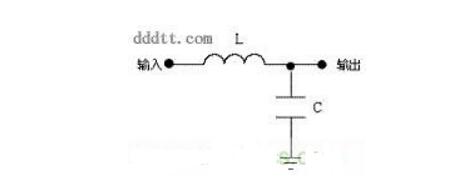
　　在线路板电源部分的电感一般是由线径非常粗的漆包线环绕在涂有各种颜色的圆形磁芯上。而且附近一般有几个高大的滤波铝电解电容，这二者组成的就是上述的LC滤波电路。另外，线路板还大量采用“蛇行线＋贴片钽电容”来组成LC电路，因为蛇行线在电路板上来回折行，也可以看作一个小电感。

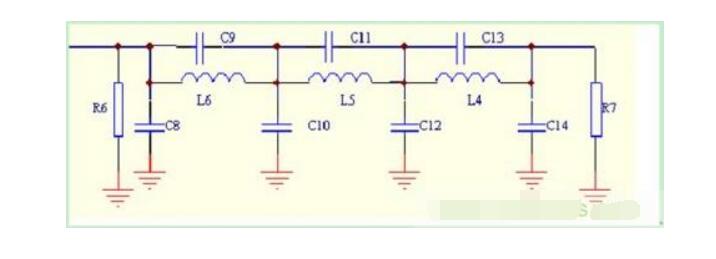
　　滤波电路的原理实际是L、c元件基本特性的组合利用。因为电容器的容抗xc=2nfc又1会随信号频率升高而变小，而电感器的感抗xl=2f会随信号频率升高而增大，如果把电容、电感进行串联、并联或混联应用，它们组合的阻抗也会随信号频率不同而发生很人变化口这表明，不同滤波电路会对某种频率信号呈现很小或很大的电抗，以致能让该频率信号顺利通过或阻碍它通过，从而起到选取某种频率信号和滤除某种频率信号的作用。

　　LC滤波电路二

　　通过电容滤被或电感滤波的分析，直流输出或多或少仍有波动。在要求较高的场合，为了得到更加平滑的直流，可以采用复式滤波器。

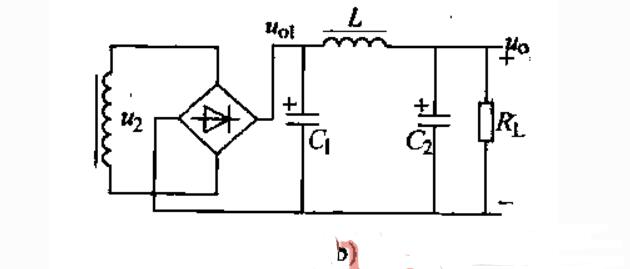
　　（1）LC滤波器我们知道t电容滤波器适用负载较大的情况，而电感滤波器适用负载较小的情况，如果把这两种电路组合起来，就构成了如图a所示的滤波器，它对于一般负载都可以适用。在LC滤波器中．脉动电压将经过双重滤波作用，使交流分量大部分被电感L阻止，即使有小部分通过了L，还要经过电容C的滤波作用使交流旁路，因此，在负载上的交流分量很小，从而达到了滤除交流的目的。

　　（2）LC-丌型滤波电路如图b所示。IJC-丌型滤渡器是由C型滤波器和LC滤波器组合而成，滤波过程t交流电整流后先经C型滤波器滤波，然后再经LC滤波器滤波．所以丌型滤波器性能比LC和C型滤波器都要优越，在Rr.上获得的电压将更平滑。

　　由于LC-7C型滤渡器前面接有电容，所以这种滤波器的外特性和电容滤波器相似。