

究竟可以怎样更简单地去理解Miller补偿呢?
描述
在一个万物生发阳光灿烂的日子里,我正规划着将要设计的电路模块。这次需要做的是一个高精度高负载调整率带片外大电容的LDO,来为整颗芯片的低压部分供电。LDO的IP是刚刚从同事那里Kiang来的,采用了Miller补偿的结构,虽然这是一个很靠谱的同事,虽然看上去其中有一些做的比较巧妙的地方,但内心不免是有些疑惑的:面对这么大的输出电容,Miller补偿真的可以吗?这颗疑问的种子其实早在一个月前就已生根发芽。完整的故事开头是这样的,曾经做过一个由DAC控制的Buffer,正负高压间ClassAB输出并带有一个10uF大电容,一般情况下空载,输出电平调整或者开关机时需要比较大的SR,那么当输出电流回归到限流值以内后可以认为开启了Settling的过程(输出不再限流表明gm退出了饱和状态),此时负载电流仍会有一个由较大值变为空载的过程,需要Buffer稳定。考虑到输出有10uF电容,大部分情况下空载,那么粗算下来输出极点频率位置会低到约0.03Hz,并且还有负载电流变化的过程,因而觉得采用Miller补偿可能会比较困难,同时考虑到高压电容的开销会很大,所以当时决定采用最土鳖的补偿办法(在敲下这段文字的当下,忽然想到其实可以采用分压和源级跟随器组合的方式把Miller电容的两端都放在低电压域,不禁感觉到一口老血要吐出来了,当年竟如此业余)。
不久前正好有人问起这个电路为什么不采用Miller补偿呢?这个电路的应用跟LDO有什么区别呢?虽然巴拉巴拉把上述考虑又搬出来讲了一番,但其实我内心疑问的小情绪已然波动起来:是啊,为什么不能采用Miller补偿呢?很多时候一提到带片外大电容的LDO,作为一个没有正儿八经做过的人,脑海里的第一印象总是先浮现出那些“ESR固定零点”、“零极点追踪”等等名词,甚至还没有经过仔细的推敲就“凭感觉”否定了Miller补偿的可能性。事实上,最近找来一些论文看过之后才发现,原来在LDO领域有大量的基于Miller补偿的设计方法和案例,还是怪自己书读的太少了啊!不过机缘巧合的是,上述问题因为前些日子的一个错误仿真而得以被仔细捋了一遍,用了尽可能简单且直观的方式把Miller效应及补偿又翻出来好好理解了一下,现在我把其中仿真错误的教训以及由此而发散的一些思考分享出来,当然有可能理解正确也有可能给出错误的解释,之所以还要厚着脸皮写出来,权当是希望可以给大家抛砖引玉,作出一点点唯小的贡献!
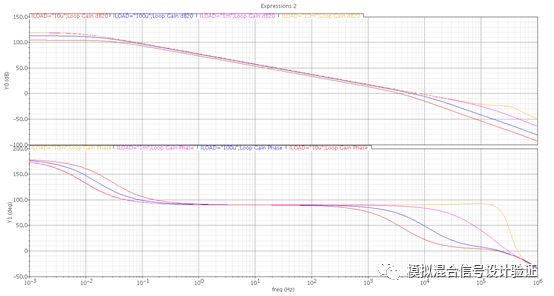
图1
好了,前戏到此结束,正片开始:拿到同事IP之后,道理我都懂,于是人狠话不多,直接上了手!但是跑完stb仿真之后如图1所示,当一根略显完美的单位增益带宽内单极点的增益曲线躺在你面前时,其实我整个人内心是不安的,原本在极低频的输出极点真的能一下子被推到单位增益带宽以外吗,即便是在几乎空载的情况下?恍惚间觉得是不是环路的断点设置错了?一直以来都是把环路断点设置在FB的高阻点,可偏偏这次不自信了,于是把断点改到了输出,得到了如图2的仿真结果。在这样的断点条件下仿真发现主极点位置能和输出极点吻合,但是却看到多了一个较近的零点和次极点。于是又一次陷入到了深深的疑惑中:次极点难道是因为负载电容太大而使Miller补偿失效了的反馈节点处的极点?那么这个零点又是个什么鬼?因为这个Miller补偿采用的是接到第一级运放折叠点cascode管源极的Ahuja接法,如图3所示,第一反应是不是这种接法有什么隐藏的Bug,比如折叠点下方电流源管漏端输出阻抗下降等。
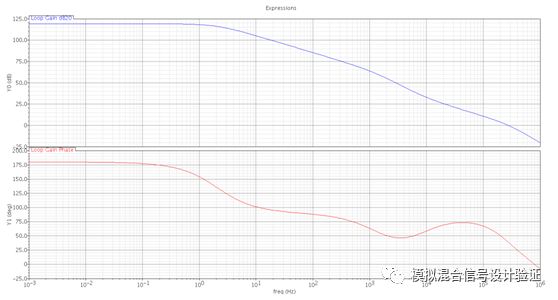
图2
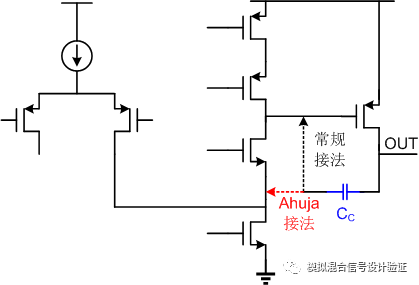
图3
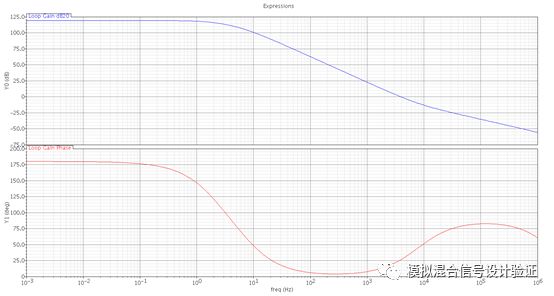
图4
于是尝试着将Ahuja接法换成常规接法,仿真stb后发现在低频有两个挨得很近的极点,如图4所示,一个频率跟输出极点吻合,另一个看起来像是Miller效应产生的极点,一度以为Ahuja接法由于某种原因让Miller补偿失效了。求助了IC群里的一些朋友,大家给出的答案也并没能尽释其中的疑惑。于是我把上述仿真到的现象跟同事一起探讨了下,刚开始他在看到波形的时候也是十分懵逼的,或者说被我先入为主的判断带沟里了。过了两天,同事发现了一个突破点,就是他用AC做闭环仿真,带宽位置是可以跟Miller补偿带宽对得上的。于是,经过与模拟设计人民的老朋友——Paper、书籍还有另一半大脑的一番深入交流之后找到了问题之所在:1.环路断点确实设错了; 2. Miller补偿在这种负载电容下还没有失效; 3. 输出极点被Miller补偿推远了。
这个结论其实非常简单,也许你会说不就是犯了个低级错误所以弄错了嘛。但是这些天仔细回顾了问题发展的整个过程,我觉得之所以会犯这样的错误,实际上还是学艺不精,并没有真正吃透Miller效应和Miller补偿的原理所致!我们常常都善于去记住一些简单的结论却没有多问一声“为什么”进而再去dig more。回到结论中的三个点,对于第一个问题,我们可能都有这样的经验,环路断的位置不对经常会出现一些异常的结果,但又不是很明确到底断在哪里是对的哪里是错的,为什么是错的,所以为保险起见常常会挑选一个高阻点,比如电阻分压反馈FB到运放输入端的栅极,抑或是同样为高阻的第一级运放输出到第二级运放输入的栅极,如图5所示。
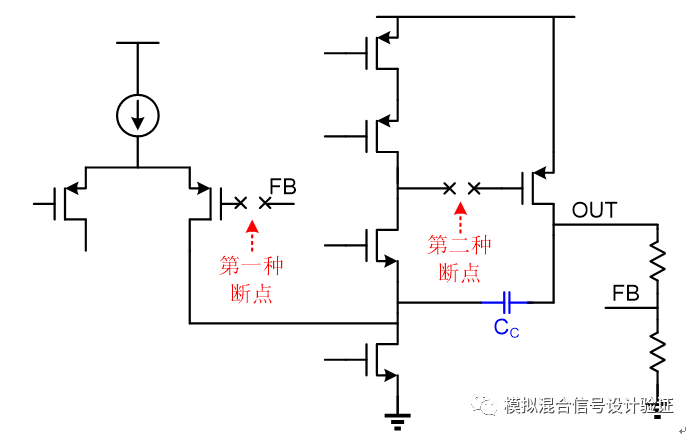
图5
对本例而言,按第一种方式断开环路是正确的,而按后者方式断开环路是错误的。那么环路究竟该如何断开才是合理的呢?从理论上而言,不管系统内部断开后某个通路归于前向通路还是反馈通路,虽然计算的环路曲线会不同,但最终计算的闭环曲线应该是能够殊途同归的。然而实际中,由于很多电路既有反馈又有前馈,同时还要考虑断点左右的负载和驱动效应,容易导致仿真器"认错",所以应该尽量保证内部嵌套的“Local loop”的完整性,断点也应尽量设置在一条接近纯数值比例的路径,比如电阻反馈到输入端的通路,使得可以比较清晰简单的来分析计算环路增益,避免仿真器迭代出一个“看起来不对”的结果。论文“ATransient-Enhanced Low-Quiescent Current Low-Dropout Regulator With BufferImpedance Attenuation”中的Fig.5很好的显示了这一特点(不过论文中Fig.5有一点小问题,重画如下图6所示)。
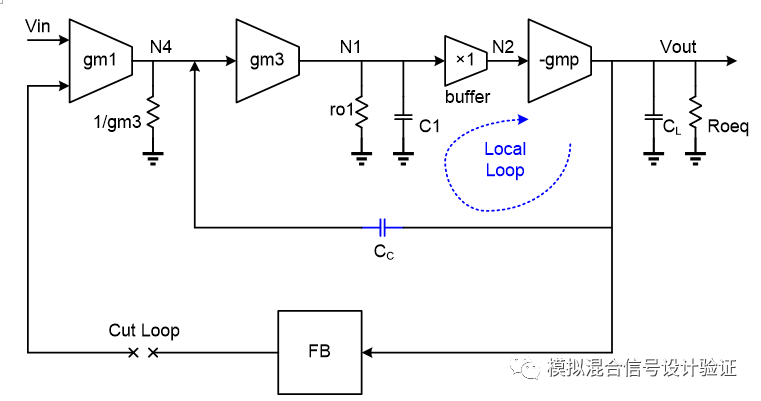
图6
所以,针对带有Miller补偿的环路,在如何设置断点这方面,我认为最为重要的原则就是保持Miller反馈小环路的完整性,并且尽可能把断点设置在常系数的路径,以免仿真器将来在报道上出现偏差!对于本例而言,上述两种断点方案之所以后者也不行是由于这种方式把带有Miller反馈的小环路给断开了(跨接电容的第二级运放栅极输入被断开了)。
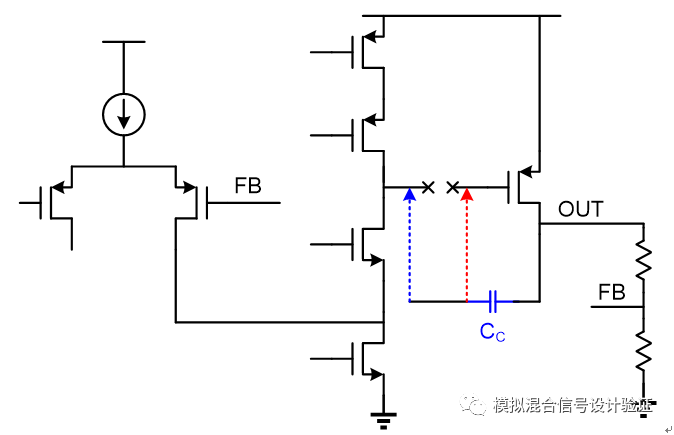
图7
假设同样是把环路断点设置在第一级运放的输出端,如图7所示仅仅只是把Miller电容的反馈端分别接到断点的左右两侧就可以得到完全不同的仿真结果,这就是因为接回到断点右侧时保持了Miller小环路的完整性。上文提到了两种不同接法的Miller补偿仿真得到了两个巨大差异的结果,也是因为环路断点被错误的设置在了LDO输出端(尝试过断点设置在第一级运放输出端也是同样的结果,除非Miller反馈接回点在环路断点的右侧从而保持小环路完整)。由于断点破坏了Miller补偿所在小环路,所以两种不同接法的Miller补偿电路仿真得到的主极点都变成了输出极点,而次极点在电路中的位置处于电容反馈端,Ahuja的接法电容反馈端接的是低阻点,因此相比于另一种接法所看到的次极点要远得多。之所以要保证Local Loop的完整性是由于其输入输出阻抗由于反馈的作用发生了改变,这个小环路是作为一个整体接入到前向通路中的,如果将其断开将无法获得这一特性,因而影响了整条路径的计算结果,在看完整篇文章的分析后会使你有一个更清晰的认识。
对于前文所提出的第二和第三个结论,实际上可以归结为同一个问题,也就是Miller极点跟输出极点的关系,简单来说是不是当Miller极点与输出极点相近时就认为Miller补偿失效了?我们都知道,采用Miller补偿时不仅仅会产生一个Miller极点,同时还会让主次极点分离。Miller效应会使得在电容所跨接的运放输入端看到了一个被放大了AM倍的等效电容(AM是跨接在电容两端运放的开环增益),但是仅仅只做这样一个理解实在是太过于简单粗陋了。另一方面,当输出负载电容增大时,会使得Miller电容两端所跨接的运放增益在相同频率下变得更小,导致这个增益会在更低的频率点下降到1。至于输出负载电容大到多少,或者说上述增益下降到多少会另Miller补偿失效,许多课程和书上并没有给出一个很好的判断标准,常常以“输出电容非常大”就一带而过了。至于说两个极点的分离机制,Razavi和Sansen的书都只扔出了公式,没有给出从电路原理的角度去分析这个问题的简单方法。总之,当初在遇到问题的过程中,既没有清晰地理解透彻Miller效应,也没有梳理清楚Miller补偿的机制,从而造成了许多困惑和不解。
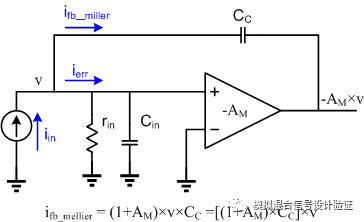
图8
如图8所示,Miller效应及其电容等效的原理最经典的解释就是当输入有一个电压变化时,由于放大器的作用在输出产生了一个-AM倍的电压变化,于是在电容两端看到了-(1+AM)倍的压差变化,从而使得这个电容“看上去”大了(1+AM)倍,那么就相当于在输入端等效地接了一个(1+AM)倍的电容。我们常常只关注到这个等效电容,却忽略了流过Miller电容的电流才是问题的关键!从图8中不难看出,Miller效应实质上是一种Shunt—Shunt的电压检测—电流反馈,我认为理解Miller效应最好的方式应该回归到反馈的本质,去观察各个节点电流的特性,可以获得更丰富的内容。将一个纯粹的电容与一个具有Miller效应的电容相比,之所以说等效的Miller电容要大AM倍,是由于在给定一个相同的输入变化下,Miller电容“吃掉”的电流要大AM倍,而这个倍增的系数AM则完全由跨接在Miller电容两端的放大器开环增益所决定。
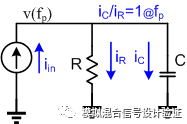
图9
那么再来看一下极点是如何定义的,如图9所示,如果从电流的角度来说,极点频率的本质实际上是指在某个节点中,让流过电容的传导电流模值与流过电阻的电流模值相等的频率点。换句话说,就是随着频率的增加,流过电容的传导电流增加,当频率增加到某一个值时,流过电容的容性特征电流(电压电流有特定的相位差)等于流过电阻的阻性电流(电压电流同相),那么这个频率就是所谓的极点频率。从电流的角度来理解一下Miller极点这个概念即为什么Miller效应可以让极点频率低AM倍。在相同的输入信号变化幅度跟观察频率下,流过Miller电容的电流会是一个纯粹的电容的AM倍,那么要达到与电阻相同的电流时,Miller电容所需要的频率自然会比一个纯粹的电容小AM倍。这样去理解Miller极点的好处是,可以很直观的来对比各种不同接法的Miller补偿间的极点位置和优缺点,比如对比Ahuja接法和电容反馈接到第一级运放输出端的传统接法。因为极点频率取决于信号电流、电阻电流跟电容电流三者间模值的关系,假定信号电流的模值是固定的,那么无论是何种接法的Miller补偿,在给定的频率下,只要流过电容的反馈电流在两种接法下保持一致或者流过电阻的误差电流保持一致,那么两者的极点频率就是相等的。Ahuja接法是在第一级运放折叠点即cascode管的源极产生误差电流,这个误差电流流过cascode管后到达第一级运放的输出,这个过程中电流增益“几乎”为1,因为从第一级输出到Miller电容另一个极板(即所接运放输出端)间的跨阻增益在两种接法下都是相同的,那么流过Miller电容的电流与电容反馈端产生的误差电流之比也“几乎”一样。如图10所示,因为反馈作用的存在,会使得误差电流跟反馈电流在两种不同的Miller补偿接法下分别相等,误差电流即流过该节点电阻的电流,那么说明两者的极点频率是一样的。
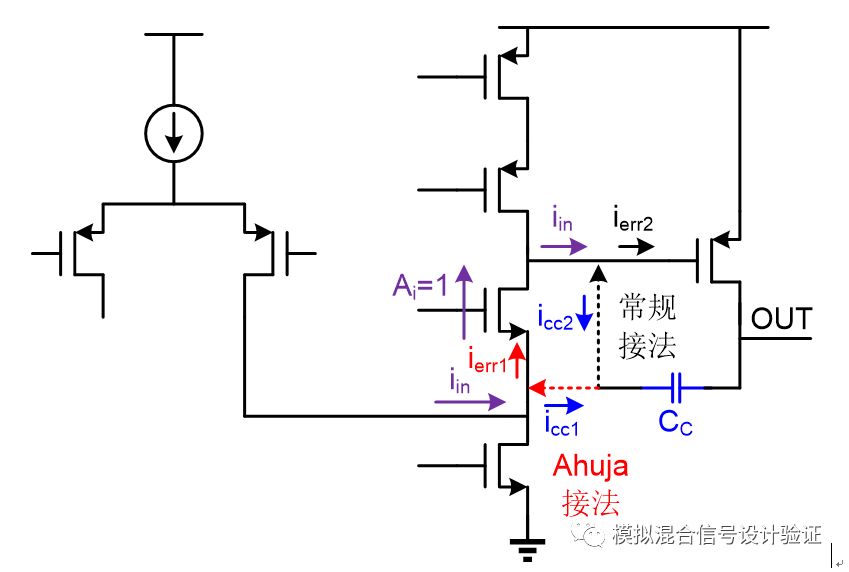
图10
我们可以进一步做一个推论:即在保持后面跨阻不变的条件下,只要Miller电容的反馈端接到通路上等电流增益的地方,这些不同的接法所得到的Miller极点频率是一样的,只是Miller极点在电路上的位置不一样(但都是在电容反馈端)。比如说在第一级运放的折叠点到第一级输出之间插入更多的cascode管,如图11所示,无论Miller电容的反馈端接到这两点间所插入的任何一个cascode管的源极,所得到的Miller极点频率是一样的(虽然第一级运放的输出电阻会增大从而使Miller极点频率相比插入cascode管前要低,但是对比电容反馈端在不同的接法下是一致的)。当然,你也可以从另一个角度来理解Ahuja接法跟传统接法两者的等效关系,比如图在10中,虽然Ahuja接法电容两端看到的运放开环增益大了gm_cas×ro1倍,但是在cascode管源极看到输出的电阻对比在第一级运放输出端看到的输出电阻要小ro1/(1/gm_cas)=gm_cas×ro1倍,所以两者抵消使得极点频率一致(gm_cas代表cascode管的跨导,ro1代表第一级运放输出端看到的输出电阻)。这样的理解实际上是不那么清晰准确的,因为达到极点频率始终取决的是相对关系而不是绝对量,隐含的条件是两种接法在同样的频率使得电容电流等于电阻电流,在输入同样的信号电流下,他们在电流求和节点处产生的电压由于输出阻抗的不同而不同。
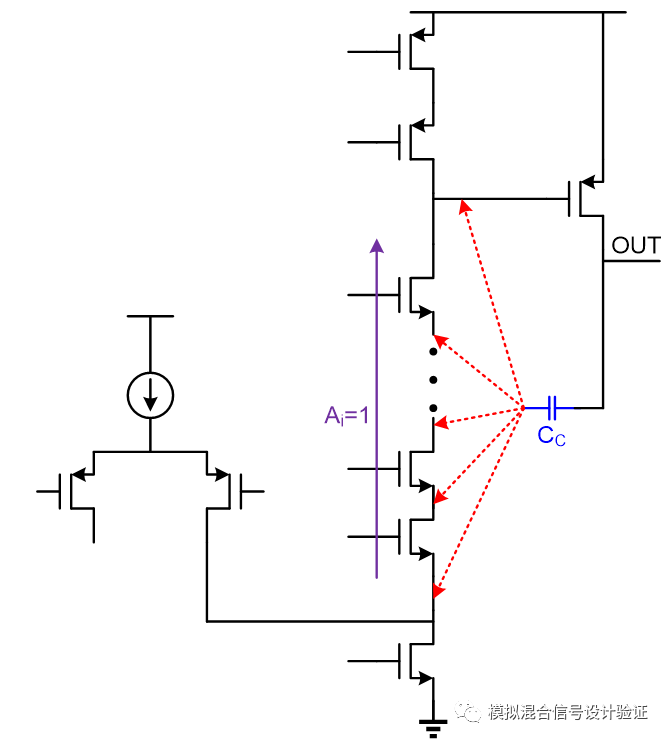
图11
一旦从电流和反馈的角度梳理清Miller效应的原理后,你会发现一切都会变得豁然开朗。显然,在Miller电容反馈端可能会接的一段通路上,寻找到通路上等电流增益的最前端是比较有效的Miller反馈接法,因为在保持Miller极点不变的情况下,跨接在电容两端的电压增益AM可能是不一样的。例如从图10中可以看到,相比于传统接法,Ahuja接法的AM要大gm_cas×ro1倍,这样会带来两个好处:一由于反馈和低阻点的关系让启动建立的过程更容易;二是对输出极点的影响,也是我们下面想要讨论的另一个问题。
我们先来看如何理解极点分离这件事情,很多Paper跟书籍会直接抛出一个公式告诉你推导一下就是这么个结论,比如Sansen书中就先给了个公式和近似条件,然后再给出一个计算结果,进而得到一个结论:“如果电路中的某个参数的改变引起了系数a的改变,两个极点都会受到影响,朝着相反的方向移动,这就是极点分离的理论基础”,虽然书上也给出了一张图来描绘整个分离的轨迹过程,但是相信你看到上述文字图片时,心里仍旧会留有一句mmp的,因为既没有解释“某个参数”是哪个参数,也没有说明图中线的斜率、间距跟拐点的意义。另一方面,虽然我们知道当输出电容很大的时候Miller补偿有可能会失效,但这个“很大”究竟是多大,有没有什么判断条件呢?从反馈的角度,这个问题就变得比较容易理解了:当频率大于Miller极点频率后,Miller电容反馈系数接近于1(假设Miller补偿小环路运放输入节点寄生电容很小),此时整个反馈环路完全建立起来,环路增益T=AM×fM,只要这个频率下T足够大,那么输出等效电阻RLeq就会因为这个小环路反馈的原因而减小(1+T)倍,约为1/gmp(gmp为输出级跨导),那么输出极点就被推远了(1+T)倍,这个结论在Gray书的第九章中有具体计算。因为Miller效应导致主极点低了AM倍,而输出极点由于Miller效应被推远了约AM倍,所以总体获得了约AM2倍的极点分离。那么Miller补偿会不会失效取决于在Miller极点频率下所看到的小环路增益是不是远大于1,如图12所示可以用增益带宽积的办法来简单评估多大的AM能使得分离足够远(假定分离前miller极点比输出极点高了m倍),也就是分离后输出极点至少应该比Miller极点大DC增益ATOT倍(整个运放的总增益),即AM2/m>ATOT=gm1/CC,gm1表示第一级运放输入对的跨导,CC代表Miller电容。例如Miller电容反馈端接在第一级运放高阻输出点的时候(输出电阻为ro1),AM=gmpRL,m=(RLCL)/(ro1CC),所以CC>1/gmp×√((gm1×CL)/(ro1×RL)),其中RL和CL分别表示整个LDO输出级等效电阻和负载电容。在我们的应用条件下,CL是非常非常大的,CC相比于其所接反馈节点的寄生电容也是较大的,因此后面很多分析做了一些简化得到了一些简单的结果,本文中如不做特殊说明则默认这样的电容条件。当电路中这些容值的量级比较接近的时候,可以把这些特殊的结果中容值的部分用“退化”到实际电路下的等效电容值去替代就行。
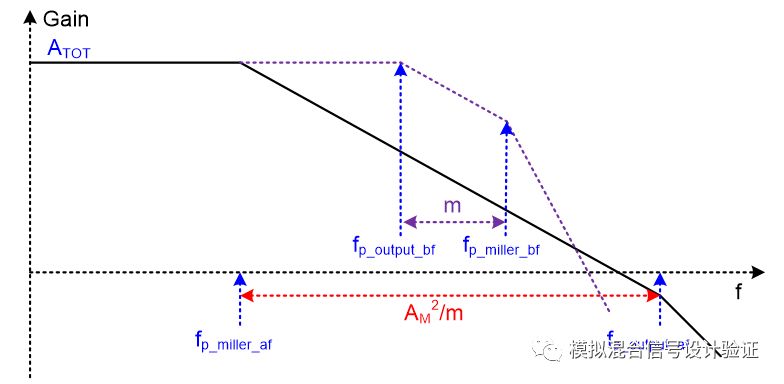
图12
看到这里,一定会有人产生这样一个疑问:输出电阻因为反馈的缘故而减小了(1+T)倍,那么输入电阻是不是也同样的会被减小(1+T)倍呢?如此一来,岂不是输入电阻的减小跟Miller电容的倍增相互“抵消”了?Gray并没有给出说明,或许是他觉得这个问题太过简单了。总之,我们知道实际中显然不是这样的结果,所以尝试着做了如下的分析。
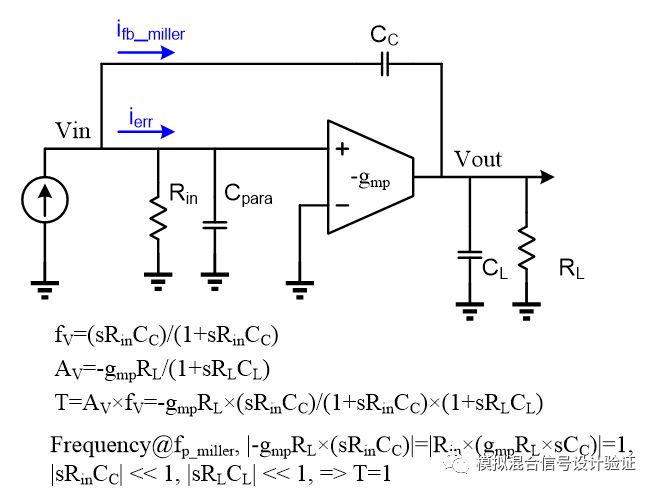
图13
我们从低频到高频来仔细的捋一下Miller补偿变化的整个过程:首先在低频时,Miller电容的反馈系数是很小的,环路增益T很小,因此绝大部分的信号电流作为误差电流流入到了运放的输入电阻,虽然也在电容两端产生了一个较大的压差,但是由于频率很低使得流过Miller电容的电流还远小于流过输入电阻上的电流。随着频率的上升,总能找到一个频率点使得流过Miller电容的电流等于流过输入电阻上的电流。此时虽然反馈系数很小,但环路增益T为1,因而几乎不会降低输入电阻,这符合原先的预期,在没有考虑负载效应的条件下如图13做了一个简化的近似计算来说明环路增益T为1的情况。随着频率的继续升高,流过输入电阻的电流越来越小,输入阻抗渐渐由输入端寄生电容占据主导,因而反馈系数很快由于电容分压的原因接近于1(考虑Miller电容远大于节点寄生电容的情况),此时的环路增益T已经足够大了,使得输入输出阻抗都被降低了(1+T)倍。但是,输入阻抗降低的是容性的部分,也就是把电容增大了(1+T)倍,对于一个电流反馈系统其看进去的输入阻抗之所以会变小,是因为在同样大小的输入电流信号下,大部分的电流被反馈网络给shunt掉了而使得进入运放的电流很小产生一个很小的输入电压。这个被反馈网络“吃”掉的电流是流入输入端看到的电容中的,属于容性成分的电流,因此这并不会改变Miller极点的位置,但却推远了输出极点!输出极点的等效阻抗被也被反馈给减小了,那为什么其s减小的是阻性阻抗而不是容性阻抗呢?首先,我们知道从输出端的角度看过去,无论Miller电容CC还是负载电容CL都没有因为反馈的作用而有“倍增”的效应,也就是说当输出电压有一个变化时,有没有这个反馈的作用流过它们的电流是一样的。那么所谓“由于反馈的作用减小了输出阻抗”到底体现在什么地方呢?这其实是由于在同样的一个电流输入信号下,由于反馈的作用,当环路增益足够大时,绝大部分输入电流通过反馈网络流到了输出,使得输入到运放的“误差电流”ierr变小了(1+T)倍,从而导致输出的电压信号相比没有反馈时小了(1+T)倍。等效的来说就是在“相同的输出电压变化下”,输出电阻+反馈网络“吃掉”的电流比没有反馈时大了(1+T)倍。虽然反馈网络shunt的电流是容性电流,但是由于整个反馈系统先遇到的是Miller极点,所以当我们把“观察频率”增加到Miller极点频率以上去寻找下一个极点时,在输出级见到的信号电流“本身就应该”是一个容性电流,也就是说Miller电容所在的反馈网络从输入端shunt过来的容性电流是和信号电流保持一致的。我们可以从另一个角度再来理解一下,即当频率高过Miller极点之后,输入端流入容性部分的电流相比于流入阻性部分的电流会越来越多,使得流入系统的输入电压信号跟电流的相位关系越来越表现出“电容性质的相位关系”,那么如果在系统输出端也展现出这样的相位关系,则表明放大器和反馈网络所组成的整体表现出了阻性的特征(保持输入输出电压电流相位关系不变)。也就是说反馈使得在输出端所看到阻抗的整个等效的阻性部分变小了,从而推远了输出极点。
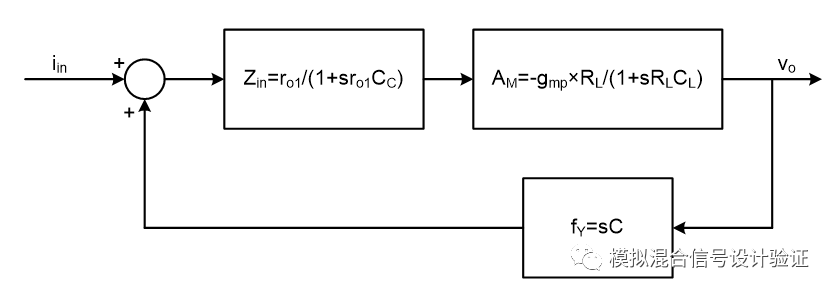
图14
图13只是一个非常简化近似的计算用来举例说明Miller极点跟输出极点随补偿的变化,下面从系统拓扑的角度来详细分析一下,如图13这样一个带有Miller电容补偿的系统结构可以用图14中的拓扑来表示。其中ro1代表图中输入电阻Rin可以看作是运放的输入电阻,假设Cpara相比CC很小可以忽略,所以系统看进去的考虑到了反馈网络负载影响后的开环输入阻抗Zin是输入电阻跟电容CC的并联。如果我们仅仅想从输入电压到输出电压的角度来看系统前向AV和反馈网络对极点分离的作用,那么我们可以做一个简单的变换得到如图15的拓扑。
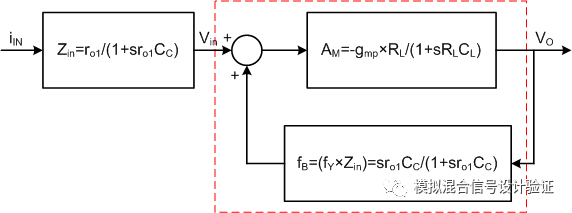
图15
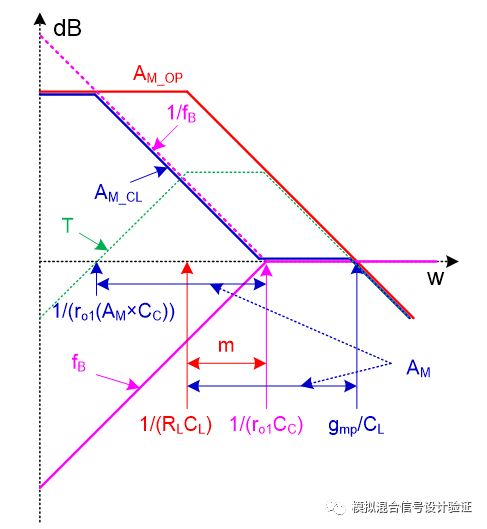
图16
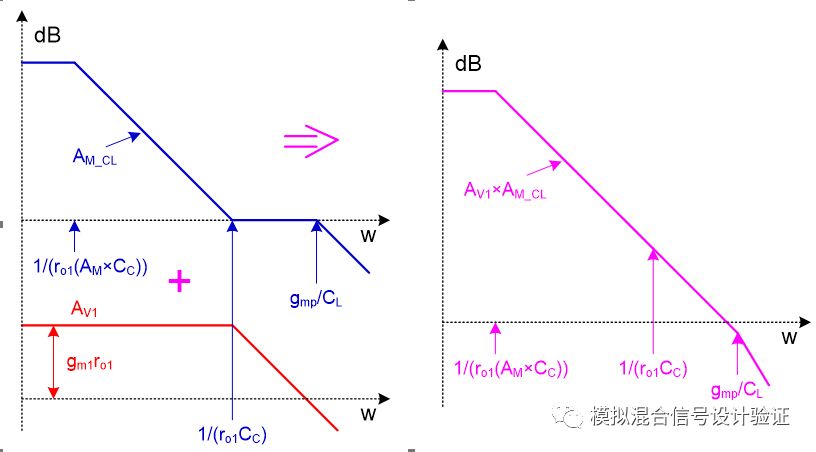
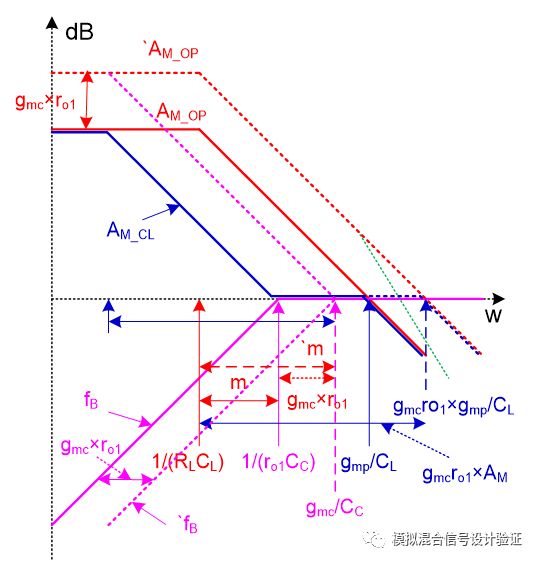
俗话说千言万语不如一张图,我们可以将图15中的各个部分如运放开环电压增益AM、反馈网络电压增益fB、其倒数1/fB、环路增益T=AM×fB还有图中红框里整个系统的闭环增益等参量随频率变化的曲线都描绘在一起,并将它们结合起来,最终可以得到Miller补偿小环路的一个近似的传递函数曲线,如图16所示。图中红色AM_OP代表跨接在Miller电容两端的运放开环增益曲线,AM代表其DC值;紫色fB表示反馈网络的增益曲线;绿色的T代表图15中红框所包含系统的环路增益曲线;蓝色AM_CL表示的就是图15中红框所包含系统的闭环增益曲线。图16中线条较多有些复杂,不过如果能将所有线条、拐点、斜率的意义搞明白,那么Miller效应和Miller补偿也就能理解的差不多了。从图中不难看出,环路增益T在Miller极点处超过1,又在被推远了的输出极点处回落到1,整个闭环系统在T远大于1时的中间部分follow曲线1/fB,在两头T远小于1时follow曲线AM_OP。所以,蓝色的闭环增益曲线具有两个极点,分别是补偿后的Miller主极点和在单位增益处的被推远了的输出次极点,整条曲线展现出的是一个“形似”积分器的形式,低频时候受限运放增益,主极点后增益单调下降直到单位增益,次级点后增益继续下降(因为只是为了观察图15中红色框里系统的特性没有将输入阻抗Zin考虑进来因而相比真正的积分器曲线有一段增益为1的平台)。从图中我们可以清晰的看到两个极点分离的情况,同时也可以印证,在断开环路做仿真时,应该保持这个带有Miller电容的补偿小环路的完整性,也就是因为反馈的原因其闭环特性需要被整体来看待。两极点最终分离之后的距离为AM2/m,试想一下将粉色反馈网络增益曲线左右移动一下,不难发现其中还隐含着Miller补偿失效的条件为m>AM,即ro1CC
图17
图18
图19
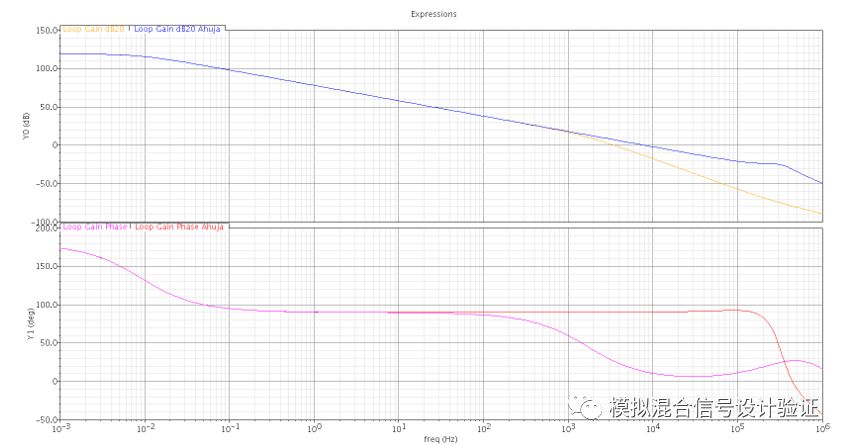
从图16出发,我们可以更进一步的来分析对比Ahuja接法的Miller补偿跟常规接法的Miller补偿,如图19所示。相对于常规接法,Ahuja接法由于电容反馈点从第一级运放输出移到了第一级运放的折叠端cascode管源极,所以跨接在电容两端的运放增益相比要大gmc×ro1倍。其中gmc表示cascode管跨导,ro1则代表了第一级运放的输出端电阻(上下两个cascode结构输出阻抗的并联),因为两个节点之间电流增益为1,所以可以知道cascode管源端的输出电阻要小gmc×ro1倍,那么从图中可以看到反馈网络的零点右移了gmc×ro1倍,从粉色实线变为了粉色虚线,同理可推其他曲线的变化,最终可以看到Miller极点的位置并没有发生改变,而输出次级点被推得更远了。至此,我们可以很清楚的理解到Ahuja接法的优势,因为Miller补偿所在环路的运放开环增益AM相比传统接法大了gmc×ro1倍,虽然图中m值也大了这么多倍,但分离后的距离为AM2/m,总体变大了gmc×ro1倍,这是由于输出极点相比被推的更远了!同样,我们也可以把前面的输入阻抗Zin和前级跨导gm1包含进来,就可以绘出类似于图18右侧这样的曲线,只是其次级点会被推得更远,这里不再累述,具体的仿真结果对比如图20所示。这里会衍生出一个问题:是不是只要往跨接在Miller电容两端的电路中间不断插入更多的cascode管就可以一直将补偿后的单位增益带宽推得更远呢?这显然是不行的,因为级联不断增加的cascode结构会在其最后一个MOS管的漏端产生一个很大的输出端阻抗引入到AM中从而使其在单位增益带宽前不再保持单极点曲线,如图19中绿线所示那样,那么就有可能影响次级点被推远的距离、带宽跟稳定性。为了让AM不引入太大的次级点,中间插入多个单级运放可能是更好的选择,因此我猜测Nested Miller补偿大概是基于这样的考虑吧,类似于多级级联的Buffer电路意图以此合理分配不同级间的驱动能力,本文里对Miller效应和补偿的一些思考相信可以对理解Nested Miller补偿有所帮助,但是具体的原理应该还是需要从Huijsing的书中去寻找答案。
图20
通过上述深入的剖析,我们可以发现从电流和反馈的角度能够更好的理解Miller效应和Miller补偿,同时也获得了一些直观的认识和结论:1. 仿真分析在断开环路时应尽量保持Miller补偿所在小环路的完整性,因为嵌套的内部闭环会对其输入输出阻抗产生影响,同时尽可能把断点设置在纯系数反馈的位置;2. Miller等效的输入电容是由跨接在其两端的运放开环增益所决定的;3.只要保持后面的跨阻一致,把Miller电容的反馈端接到跨阻前的这段通路的任何等电流增益位置,都能获得一样的Miller极点频率;4.输出极点因为Miller反馈的作用被推远了(1+T)倍,可以从增益带宽积的角度结合图12或图16来推算有效的极点分离需要多大的Miller电容和补偿小环路里多大的环路增益T,判断是不是一定可以补偿的了,在什么条件下会失效;5.Ahuja接法优点多多,暂时没有看到明显的缺点;6.通过Shift一个DC电压(比如用源极跟随器)并配合反馈系数的放大或缩小,可以将Miller电容的两端都放到合适的电压域,通过阻抗变换(还比如插入一个源极跟随器),可以隔离Miller电容的前馈效应,或者说仅引入反馈或仅引入前馈。7.可以尝试利用这些关于单个Miller反馈的思考来进一步帮助分析和简化Nested Miller补偿的原理,比如把嵌套在最里面的Miller环路作为一个整体的积分器,像图16和图18一样,一步步地“组合”出最终整个前向通路的增益曲线。
至此,虽然还不能说已经将Miller补偿完全搞懂了,但是通过一些有意义的思考还是能有效的帮助我们看清其中的一些门道,并在具体实践中提供一些有用的判据和简化计算的结果。虽然整个过程有点烧脑,但花了几个夜晚最终写出这些文字的时候感觉还是非常值得的!最后,还要感谢我的同事江文平、马吉和金津所提供的热情的帮助、探讨和给予的建议!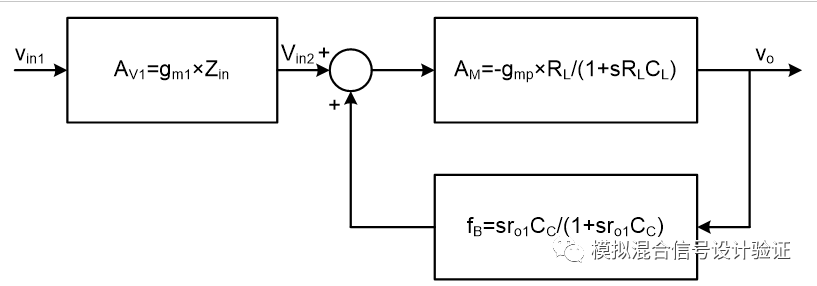
-
消除前馈通道的Miller补偿:电压跟随器2023-10-12 3801
-
浅析去补偿与完全补偿运算放大器及实现补偿的外部方法2023-09-18 3644
-
电力电容补偿的原理你究竟了解多少呢?选择用电容器进行无功补偿又有何优劣?2023-03-09 2869
-
运算放大器的补偿方法:Miller补偿2022-12-19 17357
-
怎样使用Qt去编写一个简单的上位机呢2022-03-02 1760
-
STM32的简单程序该怎样去实现呢2022-01-18 871
-
怎样去编写一个简单的stm32程序呢2021-12-15 1265
-
怎样去使用一些简单的ARM汇编指令呢2021-11-30 1750
-
怎样去设计BLDC通过IGBT进行驱动的电路呢2021-09-18 1458
-
miller补偿的第二级作用是什么?2021-06-24 922
-
内存时序究竟有多重要呢?究竟该如何去选择内存条呢?2021-06-18 2802
-
分贝究竟是什么?如何去理解它?2021-05-31 2204
-
EAGLE CAD怎样做更简单的PCB设计2019-09-10 9999
-
高精度高负载调整率带片外大电容的LDO也可以使用Miller补偿吗?2018-05-05 13219
全部0条评论

快来发表一下你的评论吧 !

