基于密度DBSCAN的聚类算法

　　聚类算法概念

　　聚类分析又称群分析，它是研究（样品或指标）分类问题的一种统计分析方法，同时也是数据挖掘的一个重要算法。聚类（Cluster）分析是由若干模式（Pattern）组成的，通常，模式是一个度量（Measurement）的向量，或者是多维空间中的一个点。聚类分析以相似性为基础，在一个聚类中的模式之间比不在同一聚类中的模式之间具有更多的相似性。

　　聚类的用途是很广泛的。在商业上，聚类可以帮助市场分析人员从消费者数据库中区分出不同的消费群体来，并且概括出每一类消费者的消费模式或者说习惯。它作为数据挖掘中的一个模块，可以作为一个单独的工具以发现数据库中分布的一些深层的信息，并且概括出每一类的特点，或者把注意力放在某一个特定的类上以作进一步的分析；并且，聚类分析也可以作为数据挖掘算法中其他分析算法的一个预处理步骤。

　　聚类分析的算法可以分为划分法（Partitioning Methods）、层次法（Hierarchical Methods）、基于密度的方法（density-based methods）、基于网格的方法（grid-based methods）、基于模型的方法（Model-Based Methods）。

　　聚类算法的分类

　　划分法

　　划分法（partitioning methods），给定一个有N个元组或者纪录的数据集，分裂法将构造K个分组，每一个分组就代表一个聚类，K《N。而且这K个分组满足下列条件：

　　（1） 每一个分组至少包含一个数据纪录；

　　（2）每一个数据纪录属于且仅属于一个分组（注意：这个要求在某些模糊聚类算法中可以放宽）；

　　对于给定的K，算法首先给出一个初始的分组方法，以后通过反复迭代的方法改变分组，使得每一次改进之后的分组方案都较前一次好，而所谓好的标准就是：同一分组中的记录越近越好，而不同分组中的纪录越远越好。

　　大部分划分方法是基于距离的。给定要构建的分区数k，划分方法首先创建一个初始化划分。然后，它采用一种迭代的重定位技术，通过把对象从一个组移动到另一个组来进行划分。一个好的划分的一般准备是：同一个簇中的对象尽可能相互接近或相关，而不同的簇中的对象尽可能远离或不同。还有许多评判划分质量的其他准则。传统的划分方法可以扩展到子空间聚类，而不是搜索整个数据空间。当存在很多属性并且数据稀疏时，这是有用的。为了达到全局最优，基于划分的聚类可能需要穷举所有可能的划分，计算量极大。实际上，大多数应用都采用了流行的启发式方法，如k-均值和k-中心算法，渐近的提高聚类质量，逼近局部最优解。这些启发式聚类方法很适合发现中小规模的数据库中小规模的数据库中的球状簇。为了发现具有复杂形状的簇和对超大型数据集进行聚类，需要进一步扩展基于划分的方法。 

　　使用这个基本思想的算法有：K-MEANS算法、K-MEDOIDS算法、CLARANS算法；

　　层次法

　　层次法（hierarchical methods），这种方法对给定的数据集进行层次似的分解，直到某种条件满足为止。具体又可分为“自底向上”和“自顶向下”两种方案。

　　例如，在“自底向上”方案中，初始时每一个数据纪录都组成一个单独的组，在接下来的迭代中，它把那些相互邻近的组合并成一个组，直到所有的记录组成一个分组或者某个条件满足为止。

　　层次聚类方法可以是基于距离的或基于密度或连通性的。层次聚类方法的一些扩展也考虑了子空间聚类。层次方法的缺陷在于，一旦一个步骤（合并或分裂）完成，它就不能被撤销。这个严格规定是有用的，因为不用担心不同选择的组合数目，它将产生较小的计算开销。然而这种技术不能更正错误的决定。已经提出了一些提高层次聚类质量的方法。 

　　代表算法有：BIRCH算法、CURE算法、CHAMELEON算法等；

　　密度算法

　　基于密度的方法（density-based methods），基于密度的方法与其它方法的一个根本区别是：它不是基于各种各样的距离的，而是基于密度的。这样就能克服基于距离的算法只能发现“类圆形”的聚类的缺点。

　　这个方法的指导思想就是，只要一个区域中的点的密度大过某个阈值，就把它加到与之相近的聚类中去。

　　代表算法有：DBSCAN算法、OPTICS算法、DENCLUE算法等；

　　图论聚类法

　　图论聚类方法解决的第一步是建立与问题相适应的图，图的节点对应于被分析数据的最小单元，图的边（或弧）对应于最小处理单元数据之间的相似性度量。因此，每一个最小处理单元数据之间都会有一个度量表达，这就确保了数据的局部特性比较易于处理。图论聚类法是以样本数据的局域连接特征作为聚类的主要信息源，因而其主要优点是易于处理局部数据的特性。

　　网格算法

　　基于网格的方法（grid-based methods），这种方法首先将数据空间划分成为有限个单元（cell）的网格结构，所有的处理都是以单个的单元为对象的。这么处理的一个突出的优点就是处理速度很快，通常这是与目标数据库中记录的个数无关的，它只与把数据空间分为多少个单元有关。

　　代表算法有：STING算法、CLIQUE算法、WAVE-CLUSTER算法；

　　模型算法

　　基于模型的方法（model-based methods），基于模型的方法给每一个聚类假定一个模型，然后去寻找能够很好的满足这个模型的数据集。这样一个模型可能是数据点在空间中的密度分布函数或者其它。它的一个潜在的假定就是：目标数据集是由一系列的概率分布所决定的。

　　通常有两种尝试方向：统计的方案和神经网络的方案。

　　基于密度DBSCAN的聚类算法

　　DBSCAN算法的原理

　　1、基本概念

　　DBSCAN（Density-BasedSpatialClusteringofApplicationwithNoise）是一种典型的基于密度的聚类算法，在DBSCAN算法中将数据点分为一下三类：

　　核心点。在半径Eps内含有超过MinPts数目的点

　　边界点。在半径Eps内点的数量小于MinPts，但是落在核心点的邻域内

　　噪音点。既不是核心点也不是边界点的点

　　在这里有两个量，一个是半径Eps，另一个是指定的数目MinPts。

　　其他的概念

　　1）Eps邻域。简单来讲就是与点p的距离小于等于Eps的所有的点的集合，可以表示为。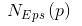

　　2）直接密度可达。如果p在核心对象q的Eps邻域内，则称对象p从对象q出发是直接密度可达的。

　　3）密度可达。对于对象链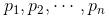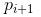：，是从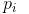关于Eps和MinPts直接密度可达的，则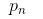对象是从对象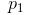关于Eps和MinPts密度可达的。

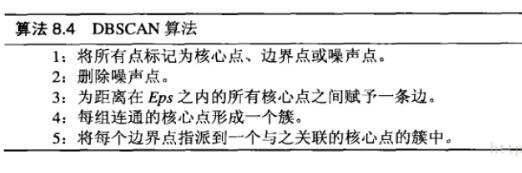
　　2、算法流程

　　实验仿真

　　在实验中使用了两个测试数据集，数据集的原始图像如下：

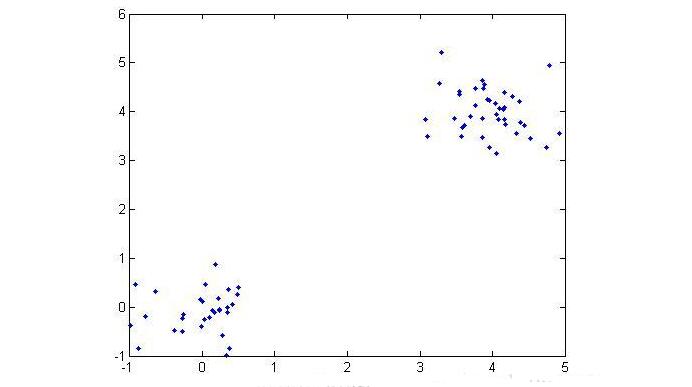
　　（数据集1）

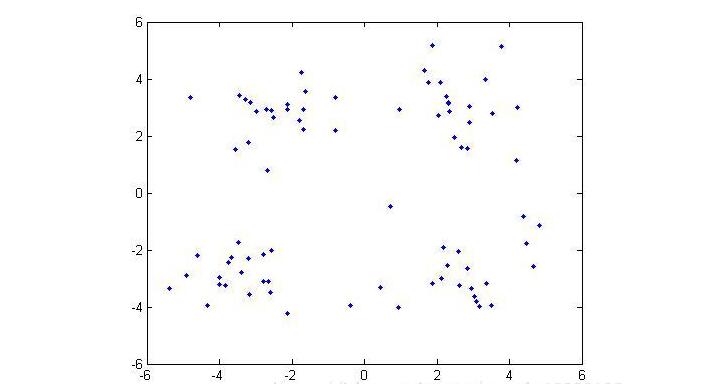
　　（数据集2）

　　数据集1相对比较简单。显然我们可以发现数据集1共有两个类，数据集2有四个类，下面我们通过DBSCAN算法实现数据点的聚类：

　　MATLAB代码

　　主程序

　　%% DBSCAN

　　clear all;

　　clc;

　　%% 导入数据集

　　% data = load（‘testData.txt’）;

　　data = load（‘testData_2.txt’）;

　　% 定义参数Eps和MinPts

　　MinPts = 5;

　　Eps = epsilon（data， MinPts）;

　　［m，n］ = size（data）;%得到数据的大小

　　x = ［（1:m）‘ data］;

　　［m，n］ = size（x）;%重新计算数据集的大小

　　types = zeros（1，m）;%用于区分核心点1，边界点0和噪音点-1

　　dealed = zeros（m，1）;%用于判断该点是否处理过，0表示未处理过

　　dis = calDistance（x（：，2:n））;

　　number = 1;%用于标记类

　　%% 对每一个点进行处理

　　for i = 1:m

　　%找到未处理的点

　　if dealed（i） == 0

　　xTemp = x（i，：）;

　　D = dis（i，：）;%取得第i个点到其他所有点的距离

　　ind = find（D《=Eps）;%找到半径Eps内的所有点

　　%% 区分点的类型

　　%边界点

　　if length（ind） 》 1 && length（ind） 《 MinPts+1

　　types（i） = 0;

　　class（i） = 0;

　　end

　　%噪音点

　　if length（ind） == 1

　　types（i） = -1;

　　class（i） = -1;

　　dealed（i） = 1;

　　end

　　%核心点（此处是关键步骤）

　　if length（ind） 》= MinPts+1

　　types（xTemp（1，1）） = 1;

　　class（ind） = number;

　　% 判断核心点是否密度可达

　　while ~isempty（ind）

　　yTemp = x（ind（1），：）;

　　dealed（ind（1）） = 1;

　　ind（1） = ［］;

　　D = dis（yTemp（1，1），：）;%找到与ind（1）之间的距离

　　ind_1 = find（D《=Eps）;

　　if length（ind_1）》1%处理非噪音点

　　class（ind_1） = number;

　　if length（ind_1） 》= MinPts+1

　　types（yTemp（1，1）） = 1;

　　else

　　types（yTemp（1，1）） = 0;

　　end

　　for j=1:length（ind_1）

　　if dealed（ind_1（j）） == 0

　　dealed（ind_1（j）） = 1;

　　ind=［ind ind_1（j）］;

　　class（ind_1（j））=number;

　　end

　　end

　　end

　　end

　　number = number + 1;

　　end

　　end

　　end

　　% 最后处理所有未分类的点为噪音点

　　ind_2 = find（class==0）;

　　class（ind_2） = -1;

　　types（ind_2） = -1;

　　%% 画出最终的聚类图

　　hold on

　　for i = 1:m

　　if class（i） == -1

　　plot（data（i，1），data（i，2），’.r‘）;

　　elseif class（i） == 1

　　if types（i） == 1

　　plot（data（i，1），data（i，2），’+b‘）;

　　else

　　plot（data（i，1），data（i，2），’.b‘）;

　　end

　　elseif class（i） == 2

　　if types（i） == 1

　　plot（data（i，1），data（i，2），’+g‘）;

　　else

　　plot（data（i，1），data（i，2），’.g‘）;

　　end

　　elseif class（i） == 3

　　if types（i） == 1

　　plot（data（i，1），data（i，2），’+c‘）;

　　else

　　plot（data（i，1），data（i，2），’.c‘）;

　　end

　　else

　　if types（i） == 1

　　plot（data（i，1），data（i，2），’+k‘）;

　　else

　　plot（data（i，1），data（i，2），’.k‘）;

　　end

　　end

　　end

　　hold off

　　距离计算函数

　　%% 计算矩阵中点与点之间的距离

　　function ［ dis ］ = calDistance（ x ）

　　［m，n］ = size（x）;

　　dis = zeros（m，m）;

　　for i = 1:m

　　for j = i:m

　　%计算点i和点j之间的欧式距离

　　tmp =0;

　　for k = 1:n

　　tmp = tmp+（x（i，k）-x（j，k））.^2;

　　end

　　dis（i，j） = sqrt（tmp）;

　　dis（j，i） = dis（i，j）;

　　end

　　end

　　end

　　epsilon函数

　　function ［Eps］=epsilon（x，k）

　　% Function： ［Eps］=epsilon（x，k）

　　%

　　% Aim：

　　% Analytical way of estimating neighborhood radius for DBSCAN

　　%

　　% Input：

　　% x - data matrix （m，n）; m-objects， n-variables

　　% k - number of objects in a neighborhood of an object

　　% （minimal number of objects considered as a cluster）

　　［m，n］=size（x）;

　　Eps=（（prod（max（x）-min（x））*k*gamma（.5*n+1））/（m*sqrt（pi.^n）））.^（1/n）;

　　最终的结果

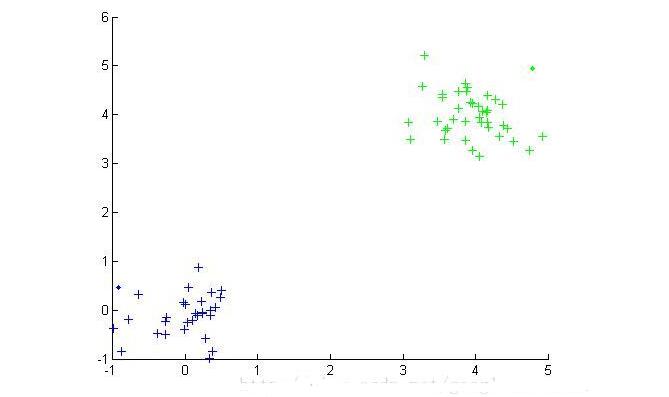
　　（数据集1的聚类结果）

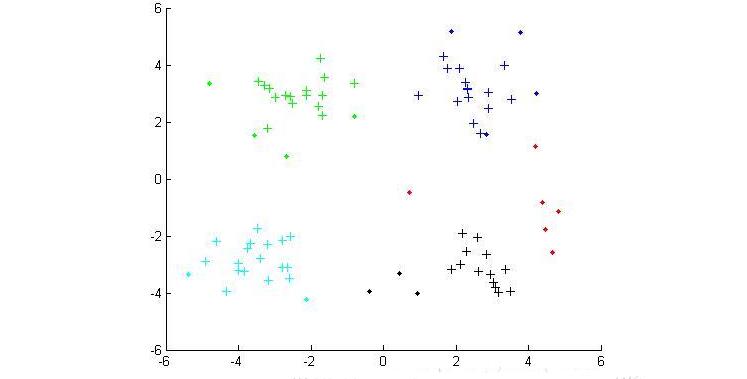
　　（数据集2的聚类结果）

　　在上面的结果中，红色的点代表的是噪音点，点代表的是边界点，十字代表的是核心点。不同的颜色代表着不同的类。