

梯度下降两大痛点:陷入局部极小值和过拟合
电子说
描述
介绍
基于梯度下降训练神经网络时,我们将冒网络落入局部极小值的风险,网络在误差平面上停止的位置并非整个平面的最低点。这是因为误差平面不是内凸的,平面可能包含众多不同于全局最小值的局部极小值。此外,尽管在训练数据上,网络可能到达全局最小值,并收敛于所需点,我们无法保证网络所学的概括性有多好。这意味着它们倾向于过拟合训练数据。
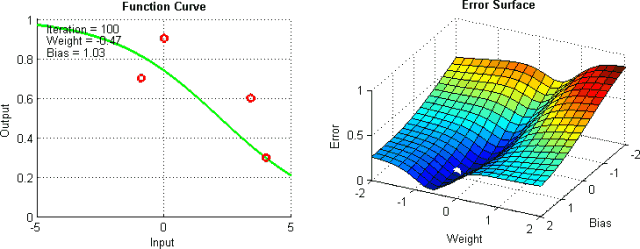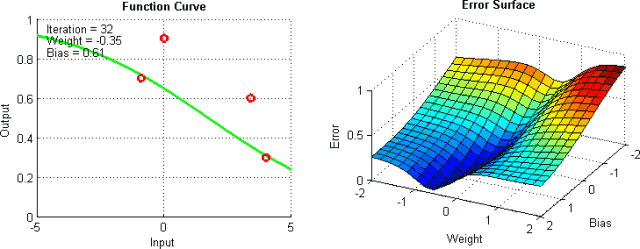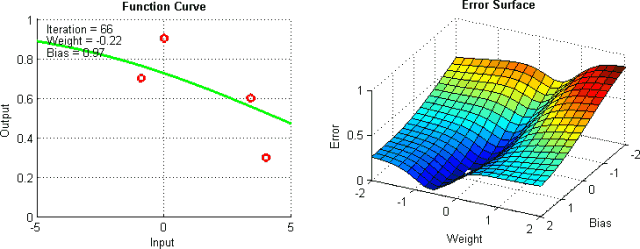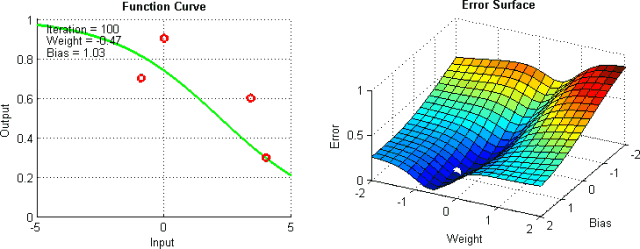
有一些手段有助于缓解这些问题,不过并没有绝对地预防这些问题产生的方法。这是因为网络的误差平面一般很难穿越,而神经网络整体而言很难解释。
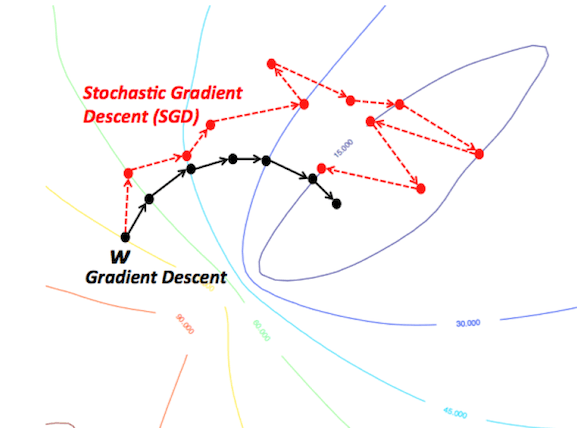
随机梯度下降与mini-batch随机梯度下降
这些算法改编了标准梯度下降算法,在算法的每次迭代中使用训练数据的一个子集。SGD在每权重更新上使用一个样本,mini-batch SGD使用预定义数目的样本(通常远小于训练样本的总数)。这大大加速了训练,因为我们在每次迭代中没有使用整个数据集,它需要的计算量少得多。同时,它也有望导向更好的表现,因为网络在训练中断断续续的移动应该能让它更好地避开局部极小值,而使用一小部分数据集当有助于预防过拟合。
正则化
正则化基本上是一个惩罚模型复杂度的机制,它是通过在损失函数中加入一个表示模型复杂度的项做到这一点的。在神经网络的例子中,它惩罚较大的权重,较大的权重可能意味着神经网络过拟合了训练数据。
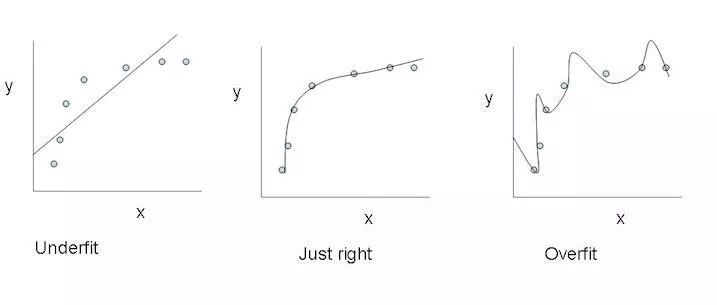
最左:欠拟合;最右:过拟合
若网络的原损失函数记为L(y, t),正则化常数记为λ,则应用了L2正则化后,损失函数改写为如下形式:
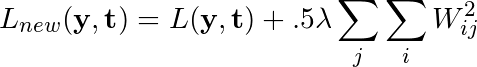
正则化在损失函数中加入了网络的每个权重的平方和,以惩罚给任何一个连接分配了过多权重的模型,希望能降低过拟合程度。
动量
简单来说,动量在当前权重更新上加上一小部分前次权重更新。这有助于预防模型陷入局部极小值,因为即使当前梯度为0,之前梯度绝大多数情况下不为0,这样模型就不那么容易陷入极小值。另外,使用动量也使误差平面上的移动总体上更为平滑,而且移动得更快。
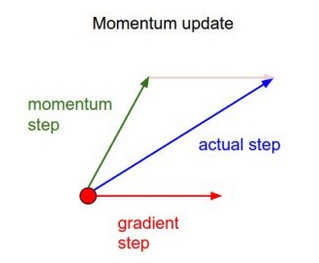
基于这一简单的动量概念,我们可以重写权重更新等式至如下形式(α为动量因子):
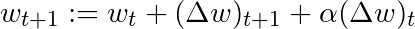
还有其他一些更高级的动量形式,比如Nesterov方法。
学习率退火
我们可以不在整个训练过程中使用同一学习率,而是随着时间的进展降低学习率,也就是退火。
最常见的退火规划基于1/t关系,如下图所示,其中T和μ0为给定的超参数,μ为当前学习率:
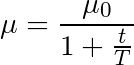
这经常被称为“搜索并收敛”(search-then-converge)退火规划,因为直到t达到T之前,网络都处于“搜索”阶段,学习率没有下降很多,在此之后,学习率减慢,网络进入“收敛”阶段。这和探索(exploitation)与利用(exploration)间的平衡多多少少有些关系。刚开始我们优先探索搜索空间,扩展我们关于空间的整体知识,随着时间的推进,我们过渡到利用搜索空间中我们已经找到的良好区域,收缩至特定的极小值。
结语
这些改进标准梯度下降算法的方法都需要在模型中加入超参数,因而会增加调整网络所需的时间。最近提出的一些新算法,比如Adam、Adagrad、Adadelta,倾向于在每个参数的基础上进行优化,而不是基于全局优化,因此它们可以基于单独情况精细地调整学习率。在实践中,它们往往更快、更好。下图同时演示了之前提到的梯度下降变体的工作过程。注意看,和简单的动量或SGD相比,更复杂的变体收敛得更快。
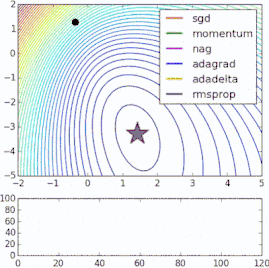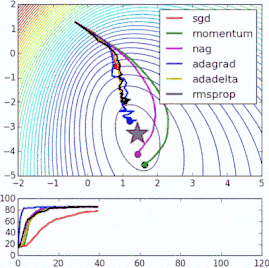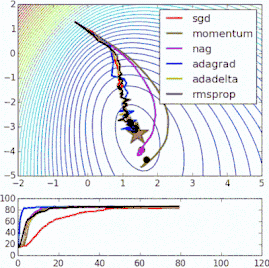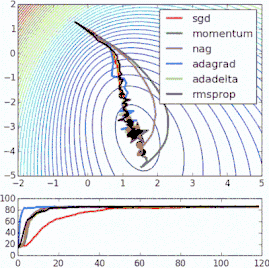
-
SGD的随机项在其选择最终的全局极小值点的关键性作用2019-03-06 5921
-
分享一个自己写的机器学习线性回归梯度下降算法2018-10-02 5112
-
机器学习新手必学的三种优化算法(牛顿法、梯度下降法、最速下降法)2019-05-07 5861
-
如何更新权重实现梯度下降2019-07-15 2575
-
机器学习:随机梯度下降和批量梯度下降算法介绍2017-11-28 9997
-
梯度下降算法及其变种:批量梯度下降,小批量梯度下降和随机梯度下降2018-05-03 22850
-
讲解随机梯度下降、类别数据编码、Vowpal Wabbit机器学习库2018-07-17 6862
-
简单的梯度下降算法,你真的懂了吗?2018-09-19 1162
-
如何使用区域相似度实现局部拟合活动轮廓模型2021-03-12 1192
-
基于双曲网络空间嵌入与极小值聚类的社区划分算法2021-04-01 1629
-
基于局部熵拟合与全局信息的改进活动轮廓模型2021-05-26 1069
-
JPEG LS算法局部梯度值计算原理2024-04-25 1117
全部0条评论

快来发表一下你的评论吧 !

