

一种能够平滑衔接无模型和基于模型策略的强化学习算法
电子说
描述
试想一下我们希望从伯克利大学骑车到金门大桥,虽然仅仅只有二十公里之遥,但如果却面临一个天大的问题:你从来没有骑过自行车!而且雪上加霜的是,你刚刚来到湾区对于路况很陌生,手头仅仅只有一张市区的地图。那我们该如何骑车去看心心念念的金门大桥呢?这个看似十分复杂的任务却是机器人利用强化学习需要解决的问题。
让我们先来看看如何学会骑自行车。一种方法是先尽可能多的学习知识并一步步的规划自己的行为来实现骑车这一目标:通过读如何骑自行车的书、学习相关的物理知识、规划骑车时每一块肌肉的运动...这种一板一眼的方式在研究中还可行,但是要是用来学习自行车那永远也到不了金门大桥了。学习自行车正确的姿势是不断地尝试不断地试错和练习。像学习骑自行车这样太复杂的问题是不能通过实现规划实现的。
当你学会骑车之后,下一步便是如果从伯克利到金门大桥了。你可以继续利用试错的策略尝试各种路径看看终点是不是在金门大桥。但这种方式显而易见的缺点是我们可能需要十分十分久的时间才能到达。那么对于这样简单的问题,基于已有的信息规划便是一种十分有效的策略了,无需太多真实世界的经验和试错便能完成。在强化学习中意味着更加高效采样的学习过程。
对于一些技能来说试错学习十分有效,而对于另一些规划却来得更好
上面的例子虽然简单但却反映了人类智慧的重要特征,对于某些任务我们选择利用试错的方式,而某些任务则基于规划来实现。同样在强化学习中不同的方法也适用于不同的任务。
然而在上面的例子中两种方法却不是完全独立的,事实上如果用试错的方法来概括自行车的学习过程就太过于简单了。当我们利用试错的方法来学习自行车时,我们也利用了一点点规划的方法。可能在一开始的时候你的计划是不要摔倒,而后变为了不要摔倒地骑两米。最后当你的技术不断提高后,你的目标会变成更为抽象的概念比如要骑到道路的尽头哦,这时候需要更多关注的是如何规划这一目标而不是骑车的细节了。可以看到这是一个逐渐从无模型转换为基于模型策略的过程。如果能将这种策略移植到强化学习算法中,那么我们就能得到既能表现良好(最初阶段的试错方法)又具有高效采样特性(在后期转化为利用规划实现更为抽象的目标)的优秀算法了。
这篇文章中主要介绍了时域差分模型,这是一种能够平滑衔接无模型和基于模型策略的强化学习算法。接下来首先要介绍基于模型的算法是如何工作的。
基于模型的强化学习算法
在强化学习中通过动力学模型,在行为at的作用下状态将从st转化到st+1,学习的目标是最大化奖励函数r(st,a,st+1)的和。基于模型的强化学习算法假设事先给定了一个动力学模型,那么我们假设模型的学习目标是最大化一系列状态的奖励函数:

这一目标函数意味着在保证目标可行的状态下选取一系列状态和行为并最大化奖励。可行意味着每一个状态转移是有效的。例如下图中只有st+1是可行的状态。即便其他状态有更高的奖励函数但是不可行的转移也是无效的。
在我们的骑行问题中,优化问题需要规划一条从伯克利到金门大桥的路线:
上图中现实的概念很好但是却不现实。基于模型的方法利用模型f(s,a)来预测下一步的状态。在机器人中每一步十分的时间十分短暂,更实际的规划将会是像下图一样更为密集的状态转移:
回想我们每天骑自行车的过程我们的规划其实是十分抽象的过程,我们通常都会规划长期的目标而不是每一步具体的位置。而且我们仅仅在最开始的时候进行一次抽象的规划。就像刚刚讨论的那样,我们需要一个起点来进行试错的学习,并需要提供一种机制来逐渐增加计划的抽象性。于是我们引入了时域差分模型。
时域差分模型
时域差分模型一般形式为Q(s,a,sg,τ),给定当前状态、行为以及目标状态后,预测τ时间步长时主体与目标相隔的距离。直观上TDM回答了这样的问题:“如果我骑车去市中心,30分钟后我将会距离市中心多近呢?”对于机器人来说测量距离主要使用欧式距离来度量。
上图中的灰线代表了TMD算法计算出距离目标的距离。那么在强化学习中,我们可以将TMD视为在有限马尔科夫决策过程中的条件Q函数。TMD是Q函数的一种,我们可以利用无模型的方法来进行训练。一般地人们会使用深度置信策略梯度来训练TDM并对目标和时间进行回溯标记以提高算法的采样效率。理论上Q学习算法都可以用于训练TDM,但研究人员发现目前的算法更为有效。更多细节请参看论文。
利用TDM进行规划
当训练结束后我们可以利用下面的目标函数进行规划:

这里与基于模型策略不同的地方在于每K步进行一次规划,而不是每一步。等式右端的零保证了每一次状态转移轨迹的有效性:
规划就从上面的细碎的步骤变成了下图整体的,更为抽象和长期的策略:
当我们增加K时,就能获得更为长期和抽象的规划。在K步之间利用无模型的方法来选择行为,使用无模型的策略来抽象达成这些目标的过程,最后在K足够大的情况下实现了下图的规划情况,基于模型的方法用于选择抽象目标而无模型的方法则用于达到这些目标:
需要注意的是这种方法只能在K步的地方进行优化,而现实情况下却只关心某些特殊的状态(如最终状态)。
实验
研究人员们利用TMD算法进行了两个实验,首先是利用模拟的机械臂将圆柱推到目标位置:
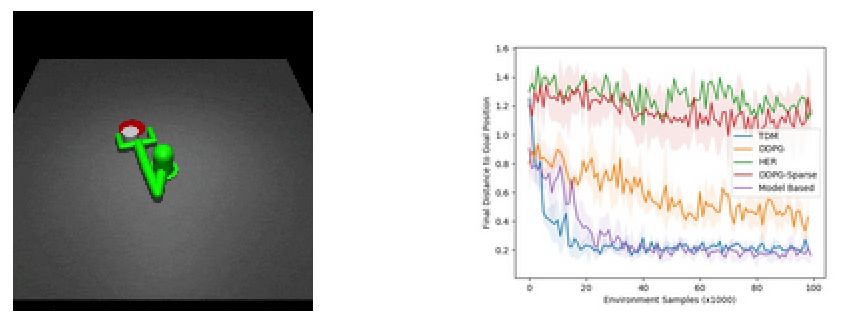
可以发现TMD算法比无模型的DDPG算法和基于模型的算法都下降的快,其快速学习能力来自于之前提到的基于模型的高效采样。
另一个实验是利用机器人进行定位的任务,下图是实验的示意图和学习曲线:
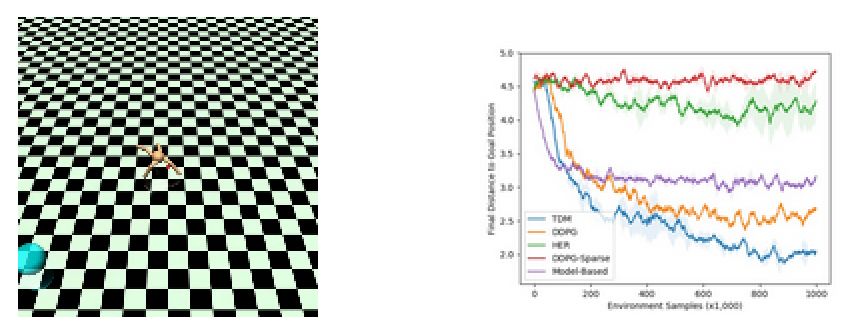
上图现实基于模型的方法在训练到一定次数后就停滞了,而基于DDPG的无模型方法则下降缓慢,但最终效果强于基于模型的方法。而TMD方法则即快速有优异,结合了上述两者的优点。
未来方向
时域差分模型为无模型和基于模型的方法提供了有效的数学描述和实现方法,但还有一系列工作需要完善。首先理论中假设环境和策略是确定的,而实际中却存在一定的随机性。这方面的研究将促进TMD对于真实环境的适应性。此外TMD可以和可选择的基于模型的规划方法结合优化。最后还希望未来将TMD用于真实机器人的定位、操作任务,甚至骑车到金门大桥去。
-
通过强化学习策略进行特征选择2024-06-05 949
-
7个流行的强化学习算法及代码实现2023-02-03 1735
-
强化学习的基础知识和6种基本算法解释2022-12-20 1647
-
一种新型的多智能体深度强化学习算法2021-06-23 898
-
基于深度强化学习仿真集成的压边力控制模型2021-05-27 966
-
模型化深度强化学习应用研究综述2021-04-12 1183
-
机器学习中的无模型强化学习算法及研究综述2021-04-08 1213
-
美国陆军研发了一种高效的地面机器人学习模型2021-01-06 2251
-
深度强化学习到底是什么?它的工作原理是怎么样的2020-06-13 7078
-
反向强化学习的思路2019-04-03 2371
-
如何构建强化学习模型来训练无人车算法2018-11-12 5421
-
斯坦福提出基于目标的策略强化学习方法——SOORL2018-06-06 5914
-
简单随机搜索:无模型强化学习的高效途径2018-04-01 4888
-
随机块模型学习算法2018-01-09 1221
全部0条评论

快来发表一下你的评论吧 !

