用74ls151实现全加器设计电路

根据全加器的定义可知：

输入为：A，B，Ci其中A，B为被加数和加数，Ci为低位进位数。

输出为：S，Co，其中S为本位和数，Co为高位进位数。

其逻辑关系为：

S=A⊕B⊕Ci

Co=AB+（A⊕B）Ci

计算后，结果用最小项表示为：

S=m1+m2+m4+m7

Co=m3+m5+m6+m7

查询74LS151和74LS138的真值表可知：

（一）74LS138

那么利用74LS138可以得到地址端A，B，Ci对应的所有最小项，然后用两个4输入与非门（74LS20）取得与上面计算得到的对应的最小项和，就能得到想要的结果。可以设计如图1所示电路：

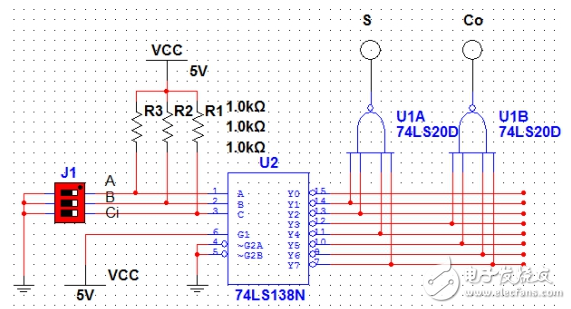
图1

图中，三位拨码开关分别代表A，B和Ci。S和Co是两个灯，代表S和Co的状态，为“1”

时亮，为“0”时不亮。

下面给出｛A=1，B=0，Ci=0｝；｛A=0，B=1，Ci=0｝；｛A=1，B=1，Ci=0｝和｛A=1，B=1，Ci=1｝四种输入状态下的S和Co状态。

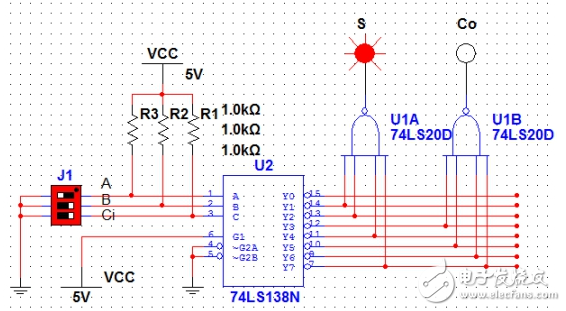
图2（A=1，B=0，Ci=0）

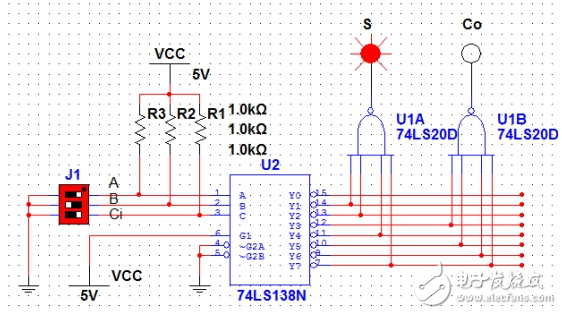
图3（A=0，B=1，Ci=0）

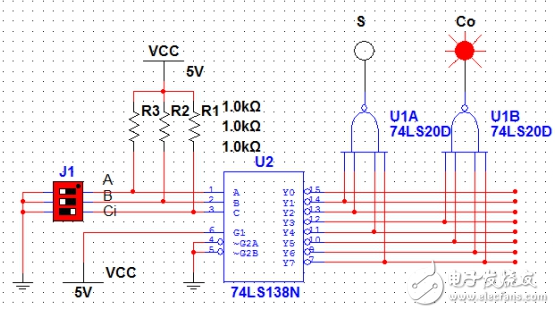
图4（A=1，B=1，Ci=0）

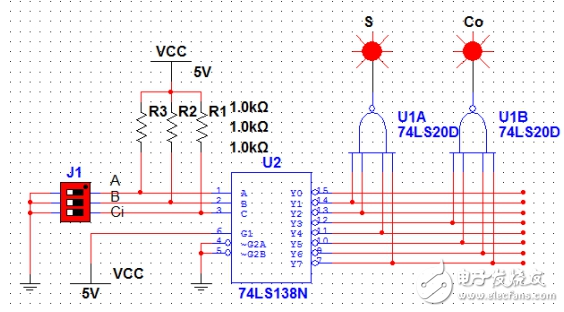
图5（A=1，B=1，Ci=1）

可以看出电路的逻辑关系是正确的。

（2）74LS151

利用74LS151数据选择器可以设计如图6所示电路：

两个74LS151分别得到S和Co；其中U1的数据端配置为D1=D2=D4=D7=1，其余为0；

U2配置为D3=D5=D6=D7=1，其余为0.

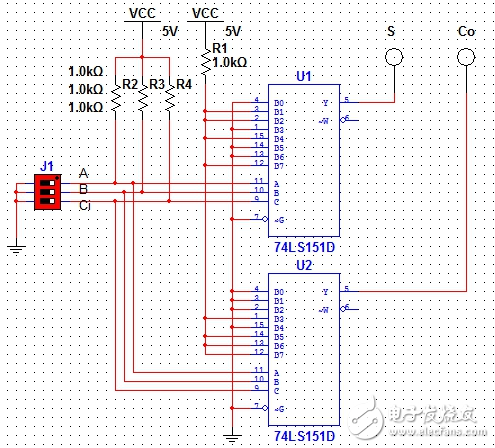
图6

同样，下面也给出{A=1，B=0，Ci=0}；｛A=0，B=1，Ci=0｝；｛A=1，B=1，Ci=0｝和｛A=1，B=1，Ci=1｝四种输入状态下的S和Co状态。

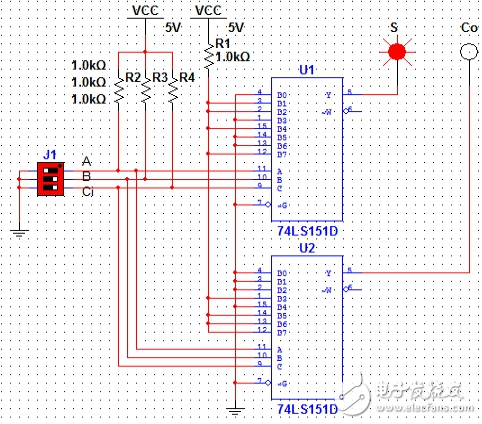
图7（A=1，B=0，Ci=0）

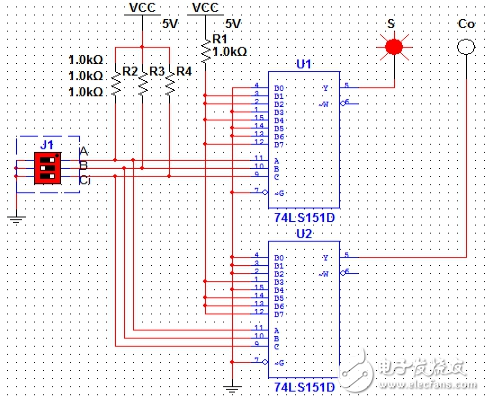
图8（A=0，B=1，Ci=0）

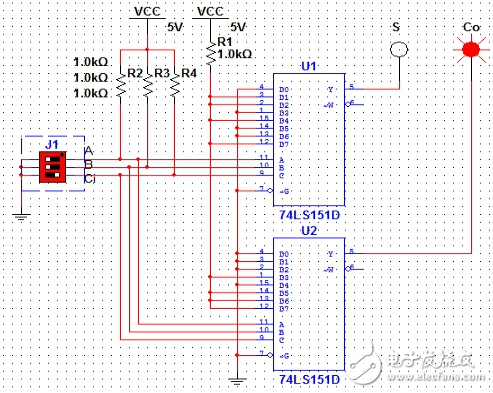
图9（A=1，B=1，Ci=0）

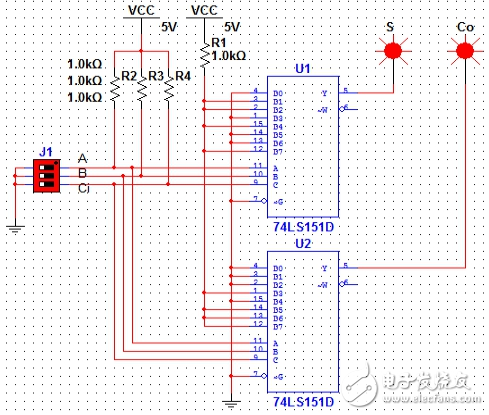
图10（A=1，B=1，Ci=1）

可以看出，电路的逻辑关系也是正确的。