细思极恐：π竟然包含了我们每个人的银行卡密码？

细思极恐

既然圆周率是无限不循环小数，那么其中是否可能包括这个世界上可用数字描述的任何信息，也就是包含了这个世界？

电话号， 生日， QQ号可能运算量比较大，但是6位的银行卡密码还是没问题的。题目本身和Pi是不是正规数没关系，但假如承认 Pi 是个正规数会有帮助

一个产生六位随机数的发生器多久能生成所有六位数？

这是赠券收集问题 ，那么期望就是 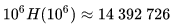 ，H 是调和级数

所以我算这么多大概就能搜索到所有的可能

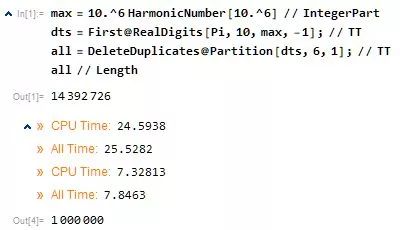
嗯，真的把十万个个全部搜出来了

加起来也就一分钟就不另外放下载了，自己跑一遍就行

当然你说要是没搜到怎么办？

这倒是有可能的，但是还是根据赠券收集原理

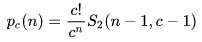
搞定的概率只有：57%

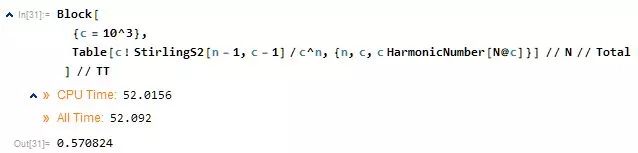
我在想这个数好眼熟....  

这个数是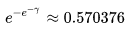 

如果要以一半概率找到生日的话需要计算3.51亿位，如果要找手机号要计算4606亿位

查了下现在的记录是22,459,157,718,361（224591亿位）， 那么找到手机号的几率>99.9%

http://www.numberworld.org/digits/Pi/#Download

另外很多网站都提供这个服务

当然一个非超越无理数以概率1是个正规数，那么同样适用这样的推理

我的生日是你的生日开平方后351084058位开始8个数字我的手机是你的手机号开立方后460653489114位开始11个数字

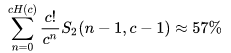
但是有个问题，斯特林数有精细结构没法给出渐进表达式

那么考虑非均匀赠券收集问题

n,i 为第$n$次选取后第$i$个样本未被选中的情形,于是概率即为相应情形之并

然后依容斥原理展开：

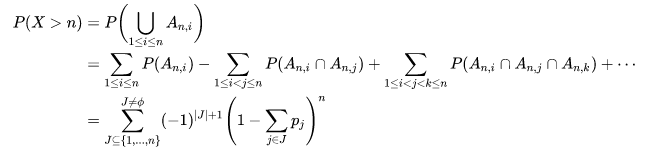
其中，$J$代表一种选法集合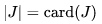， ，即集合$J$中元素的数量。

其概率生成函数为：

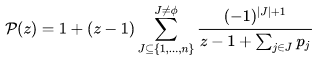
接下来对于期望而言：

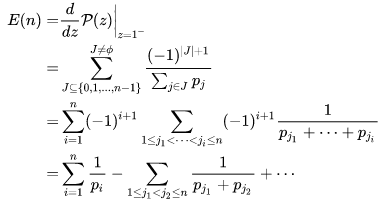
注意到  

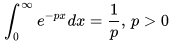
所以上式可以进一步可以写成：

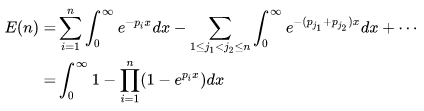
另一方面从累积分布而言：

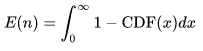
于是令 

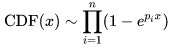
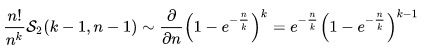
我们成功把问题转化为连续情形：

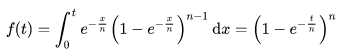
其中 n 为规模，t为计算的位数

其一阶近似就是 n H(n)

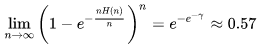
这也是临界情况，加一个微扰全部找到的概率就是1，减一个微扰概率就是0。

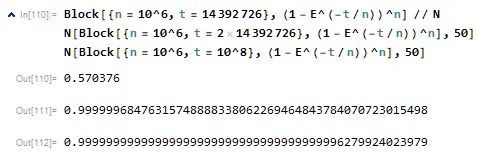
算10亿位还找不全的概率几乎为0

本文由超级数学建模编辑整理