

详解一种基于保角形变换的电磁波导波结构设计
EMC/EMI设计
描述
引言
Pendry et al.[1]提出了一个很有趣的想法,这个想法就是用坐标变换(即变换光学)的思想达到调控电磁波的能力。很不幸的是,基于坐标变换的电磁波导波器件大多数的相对介电常数和磁导率往往是非均匀各向异性材料[2][3][4],这给实现带来了很大的困难。保角形变换是光学变换的一种特例,它在二维情形下可以做到各向同性材料。在保角形变换后,拉普拉斯方程本身成了一个系数,二维亥姆霍兹方程在保角形变换后使得该系数反映在折射率的变化,也就是说在保角形变换后,如果折射率随着系数发生变化,那么满足同样的波动方程,从而达到调控电磁波的能力。在本文中,我们用基于保角形变换理论设计了一款电磁波导波结构,它的材料是非均匀各向同性的,这在实现上降低了难度。
1、保角形光学变换理论
换坐标变换前的空间为w,该空间的折射率为1;坐标变换后的空间为z,该空间的折射率为n,则z空间的折射率:[5][6] n=|dw/dz|,光学理论已经提出好几年了,虽然它的想法很新颖,但是因为根据该想法设计的大多数电磁器件的电参数为非均匀各向异性,很多学者专家不断简化参数,论文参考文献[7]根据对数保角形变换设计了可以转弯的波导转接器件,但是我们认为它并不能达到完美的转接效果,因为空间折射率的截断,必然带来散射,在本篇论文中我们基于共形变换原理设计各向同性非均匀的导波转接器件。虽然光学变换理论在导波结构中的推广已经好多年了,电参数为均匀各向异性的电磁波导波器件也已经实现,基于对数的保角形变换的导波转弯的结构也已经实现,我们认为它不能做到真正的波导转接结构,包括很复多函数在导波结构中很难应用,因为在边界的地方会发生空间折射率的截断,从而达不到完美的转接效果。在本篇论文中,我们就是通过寻找一些可行的设计函数,使得基于保角形变换的这种导波结构变得很可行。但是我们的导波结构因为函数的求解问题,导致波导的转接只能发生在一直前进的情形下,这也是我们本篇论文的局限性。我们通过将中间某个区域弯曲,而离开这个区域导波结构又恢复到原来的情形,在数学上可以表示为:
z=f(w)
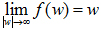 (1)
(1)
或者为
w=g(z)
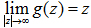 (2)
(2)
条件(1)和条件(2)只要折射率接近于一的地方截断,而中间在保角形变换后发生弯曲,就可以做到绕过在波导前进方向遇到的障碍物。
2、导波结构具体设计(单位m)
根据上面的要求我们的设计一个函数它的表达式为:
z2=w2+k (3)
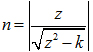 (4)
(4)
在上面的表达式中我们k=0.03。
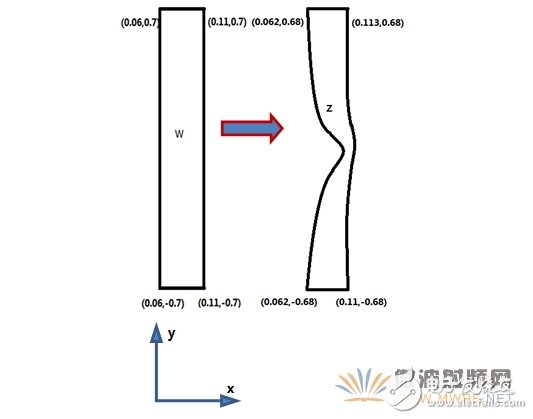
图1、w空间到z空间的变换(坐标按着上面的坐标系标注)
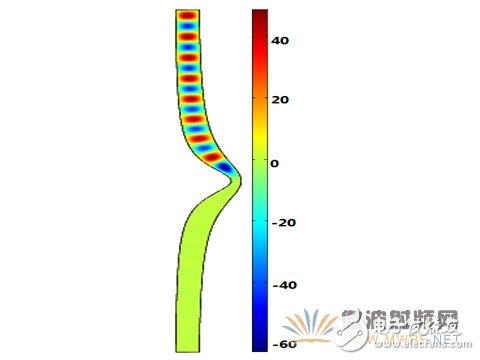
图2、保角形变换前H10模Ez分布图(f=4.6GHz)
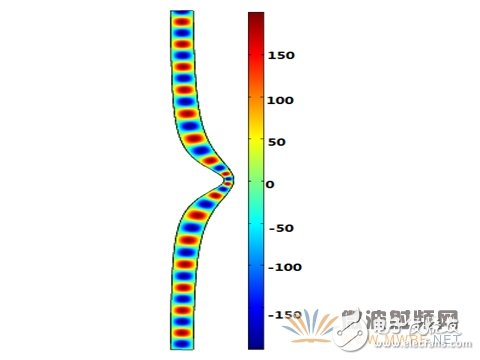
图3、保角形变换后H10模Ez分布图(f=4.6GHz)
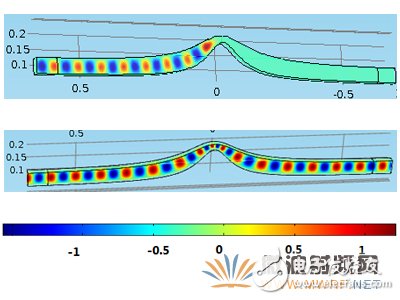
图4、三维情形下保角形变换前后H10模Ez分布图(f=4.6GHz)
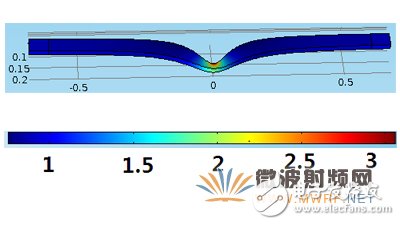
图5、三维情形下保角形变换后的折射率分布图
上面三维情况下中间为保角形变换区域,在离开光学变换区折射率接近于一的区域,高度为宽度的一半,而在横截面上与二维情形相同。两边是在折射率接近于一时截断,可以看到进行保角形变换后的可以达到非常好的波导转接结构,因为保角形变换理论是严格的根据麦克斯韦方程推导的结果,而我们只是在折射率接近于一的地方截断,所以这种导波结构只要在原来的空间的矩形波导中可以传输,那么保角形变换后仍然可以非常好的传输。从上面的实行保角形变换和不实行保角形变换对比中可以更加清楚的看出共形变换可以使波导绕过某一个区域,电磁波仍然可以很好地传输,当然,只是局限于矩形波导的H10模,但是在导波通信中矩形波导一直都是用该主模模式,所以这不能算是这种方法的局限性,只要满足方程式(1),(2)两个条件,那么运用当今的计算机技术,可以实现绕过各种形状的导波结构,我们也相信随着计算机的发展,方程的可解性提高以后,我们也可以做到任意的导波结构,因为我们没有优良的计算机,我们希望人们去探索这个问题。我们认为这种方法可以推广到介质波导中,下面这幅图的中间场集中区域和上面二维波导相同,中间的折射率由原空间的2变为现在空间的折射率:
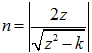
两边的区域折射率为一,频率为3GHz。
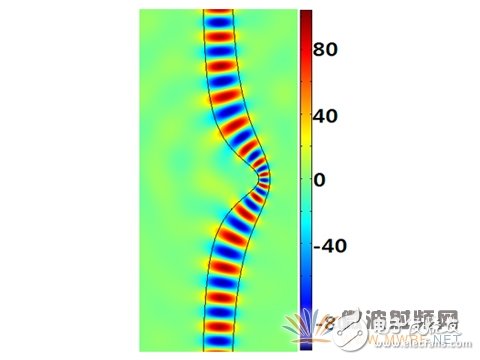
图6、二维介质波导Ez分布图
从上面的这幅图我们同样看到我们的基于共形变换的设计方法不仅局限于矩形波导,对于介质波导,如果电磁场集中于某一个区域只对该区进行保角形变换同样适用,当然,还可以用到等离子体波导中,金属的上面为介质,在等离子体波导中,金属的介电常数为负数,要使得基于保角变换的光学变换理论更有效,那么金属的介电常数绝对值要远大于介质的介电常数,保证电磁波在金属中很快的衰减,而在介质中进行共形变换。
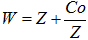 (5)
(5)
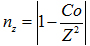 (6)
(6)
仿真参数如下:
1).Co=0.03,金属的相对介电常数为-50,原来的介质空间折射率为1,频率4GHz。
2)。原来的介质空间的几何结构如下所示:
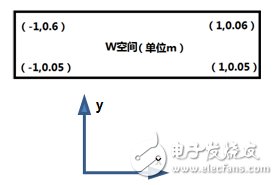
3)。上面的w空间的区域经过下面的共形变换: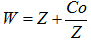 ,变成图6中间的区域,中间的折射率已经是变换后z方向电场的分布图,而两边的折射率截断后为1,从而在等离子体波导下面可以放置障碍物。
,变成图6中间的区域,中间的折射率已经是变换后z方向电场的分布图,而两边的折射率截断后为1,从而在等离子体波导下面可以放置障碍物。
仿真结果如下所示:
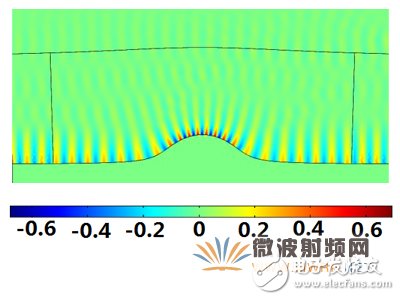
图7、二维等离子体波导进行保角形变换后的Ez分布图
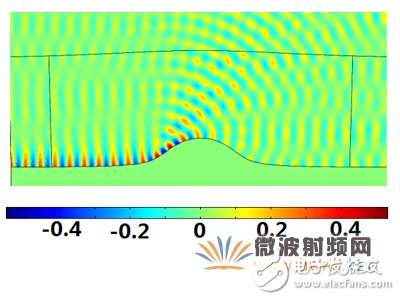
图8、二维介质波导电参数仍然保持原w空间的参数的Ez分布图
显然上面的等离子体波导是一个不实用的模型,因为它的频率非常低,金和银只有在频率远高于本仿真频率才能显示负相对介电常数,但是麦克斯韦方程本身具有的相似性原理特性,我们很容易将频率变换到对应的频率,并调整对应的几何参数和Co的大小,从上面的仿真中我们可以看到共形变换理论的价值不仅仅体现在波导中,等离子体波导中,还有介质波导中。
3、结论
本文基于保角形变换理论设计了导波结构中电磁波的在原来前进方向绕过某一个障碍物时的转接问题,可以看到这种设计方法对于可以用二维分析的场可以做到几乎非常完美的转接。这种设计方法的电参数(磁导率,相对介电常数虽然是非均匀的,但却是各向同性的。虽然折射率小于一,但是只要将电参数同时提高一定的数值,那么将会得到所有的折射率都大于一的更容易实现的设计,虽然非均匀,但是只要用离散采样的方式就可以实际做到。这种方法的局限性在于离开障碍物,必须恢复到原来空间,这也是本篇论文的主要限制。
-
一种新颖便携式机箱的结构设计2010-04-22 2336
-
操作系统结构设计2011-09-13 2512
-
谐振器——金属波导的一般特性2013-09-02 2440
-
浅谈产品结构设计特点2016-02-25 5907
-
软件结构设计2016-09-26 2519
-
一种基于保角形变换理论的电磁波导波结构设计介绍2019-06-24 2085
-
一种宽禁带圆环形PBG结构设计2019-06-27 2150
-
分享一款不错的一种基于FPGA高性能H.264变换量化结构设计2021-05-08 1611
-
导行电磁波.ppt2008-10-31 714
-
轴系结构设计实验2009-03-13 59217
-
电磁兼容结构设计2016-03-29 1246
-
如何使用坐标变换和保角形变换理论设计电磁波波导转接器件2020-09-17 1089
-
基于保角形变换的电磁波导波结构设计2022-10-21 1343
-
一种新型线性自动跟踪工频陷波器的电路结构设计2023-10-23 493
-
EMC(电磁兼容性)结构设计基础2024-08-08 769
全部0条评论

快来发表一下你的评论吧 !

