图像处理振铃效应原理_图像处理中振铃现象

　　振铃效应原理

　　振铃效应（Ringingeffect）是影响复原图像质量的众多因素之一，是由于在图像复原中选取了不适当的图像模型造成的，振铃效应产生的直接原因是图像退化过程中信息量的丢失，尤其是高频信息的丢失，其严重降低了复原图像的质量，并且使得难于对复原图像进行后续处理。

　　振铃效应是由于在图像复原中选取了不适当的图像模型造成的；在图像盲复原中如果点扩散函数选择不准确也是引起复原结果产生振铃效应的另一个原因，特别是选用的点扩散函数尺寸大于真实点扩散函数尺寸时，振铃现象更为明显；振铃效应产生的直接原因是图像退化过程中信息量的丢失，尤其是高频信息的丢失。

　　振铃效应对复原图像质量影响严重，众多学者对抑制振铃效应的方法进行了广泛研究，然而大多数图像复原方法在这一点上都有所不足，造成了复原过程中的振铃效应几乎不可避免，尤其对于有噪声存在的场合，它会混淆图像的高频特性，使得振铃效应带来的影响更加显著。

　　振铃效应产生的原因

　　频域的相乘等于空域函数的卷积，对图像做低通滤波是频域的低通滤波函数与原函数的乘积，也就是空域的低通滤波函数与原函数的卷积。理想低通的一般形式h（x）由其转移函数经傅里叶反变换得到，其曲线形似余弦函数，幅值不断变小，像素点的曲线近似为脉冲函数f（x），而卷积实际上是把脉冲函数h（x）复制到f（x）对应的位置，显然h（x）原来清晰的点被模糊了，对于复杂的图像，即产生振铃现象。

　　实际电路中减小和抑制振铃方法

　　（1）串联电阻。利用具有较大电阻的传输线或是人为地串入适当的阻尼电阻，可以减小脉冲的振幅，从而达到减小上冲和振铃程度的目的。但当传入电阻的数值过大时，不禁脉冲幅度减小过多，而且使脉冲的前沿产生延迟。因此，串入的阻尼电阻值应适当，并且应选用无感电阻，电阻的连接为值应靠近接收端。

　　（2）减小引线电感。设法减小线路及传输线的引线电感是最基本的方法，总的原则是：尽量缩短引线长度;加醋到线和印制铜箔的宽度;减小信号的传输距离，采用引线电感小的元器件等，尤其是传输前沿很陡的脉冲信号时更应注意这些问题。

　　（3）由于负载电路的等效电感和等效电容同样可以影响发送端，使之脉冲波形产生上冲和振铃，因此，应尽量减小负载电路的等效电感和电容。尤其是负载电路的接地线过长时，形成的地线电感和杂散电容相当可观，其影响不容忽视。

　　图像处理中振铃现象

　　图像处理中，对一幅图像进行滤波处理，若选用的频域滤波器具有陡峭的变化，则会使滤波图像产生“振铃”，所谓“振铃”，就是指输出图像的灰度剧烈变化处产生的震荡，就好像钟被敲击后产生的空气震荡。如下图：

　　由卷积定理可将下面两种增强联系起来：

　　频域增强：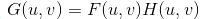

　　空域卷积：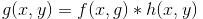

　　其中f，g，h分别为输入图像，增强图像，空域滤波函数；F，G，H分别为各自的傅里叶变换。*为卷积符号。

　　在空间域将低通滤波作为卷积过程来理解的关键是h（x，y）的特性：可将h（x，y）分为两部分：原点处的中心部分，中心周围集中的成周期分布的外围部分。前者决定模糊，后者决定振铃现象。若外围部分有明显的震荡，则g（x，y）会出现振铃。利用傅里叶变换，我们发现，若频域滤波函数具有陡峭变化，则傅里叶逆变换得到的空域滤波函数会在外围出现震荡。

　　下面给出三个常用的低通滤波器：理想型、巴特沃斯型、高斯型。并分析他们对用的空域滤波函数的特点，验证上述结论。

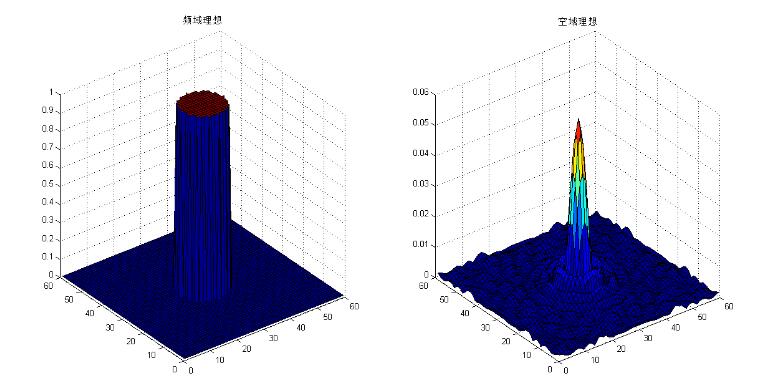
　　理想型：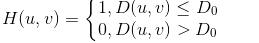

　　理想型滤波会出现振铃，可以看出空域滤波函数图像外围有剧烈震荡。

　　巴特沃斯型：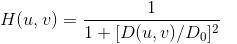

　　为阶数，1阶巴特沃斯没有“振铃“，随着阶数增大，振铃现象越发明显。下图取n=2，可以看出空域函数外围部分出现震荡。

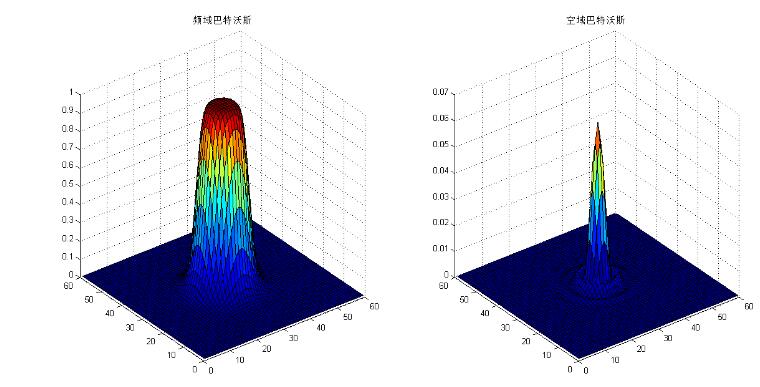
　　高斯型：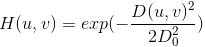

　　高斯函数的傅里叶变换仍然是高斯函数，故高斯型滤波器不会产生“振铃“。

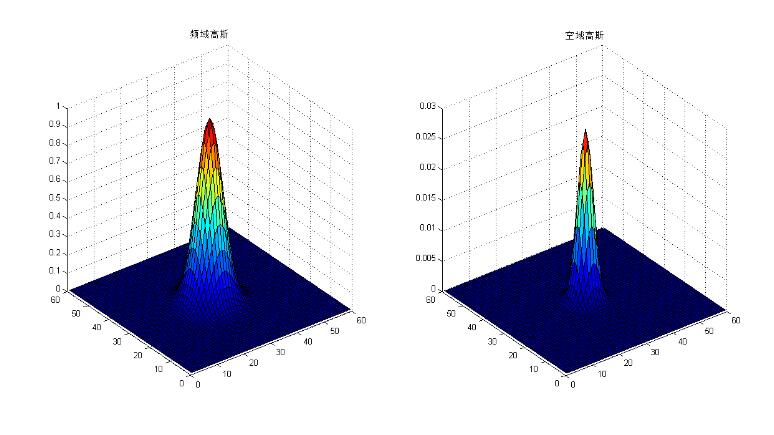
　　上述图像的生成程序：

　　［objc］ view plain copyclose all;

　　clear all;

　　d0=8;

　　M=60;N=60;

　　c1=floor（M/2）;

　　c2=floor（N/2）;

　　h1=zeros（M，N）; %理想型

　　h2=zeros（M，N）; %巴特沃斯型

　　h3=zeros（M，N）; %高斯型

　　sigma=4;

　　n=4;%巴特沃斯阶数

　　for i=1:M

　　for j=1:N

　　d=sqrt（（i-c1）^2+（j-c2）^2）;

　　if d《=d0

　　h1（i，j）=1;

　　else

　　h1（i，j）=0;

　　end

　　h2（i，j）=1/（1+（d/d0）^（2*n））;

　　h3（i，j）=exp（-d^2/（2*sigma^2））;

　　end

　　end

　　draw2（h1，‘理想’）;

　　draw2（h2，‘巴特沃斯’）;

　　draw2（h3，‘高斯’）;

　　function draw2（h，name）

　　figure;

　　surf（h）;title（strcat（‘频域’，name））;

　　fx=abs（ifft2（h））;

　　fx=fftshift（fx）;

　　figure;surf（fx）;title（strcat（‘空域’，name））;