傅里叶变换的原理及应用

01
什么是傅里叶变换？
 

一句话概括： “把复杂信号拆成多个简单正弦波的叠加。”  就像把一道混合光分解成彩虹（七色光），傅里叶变换能把任何波动信号（声音、图像、电磁波等）拆解成不同频率的“正弦波”组合。

 

02

原理：数学家的“透视眼”

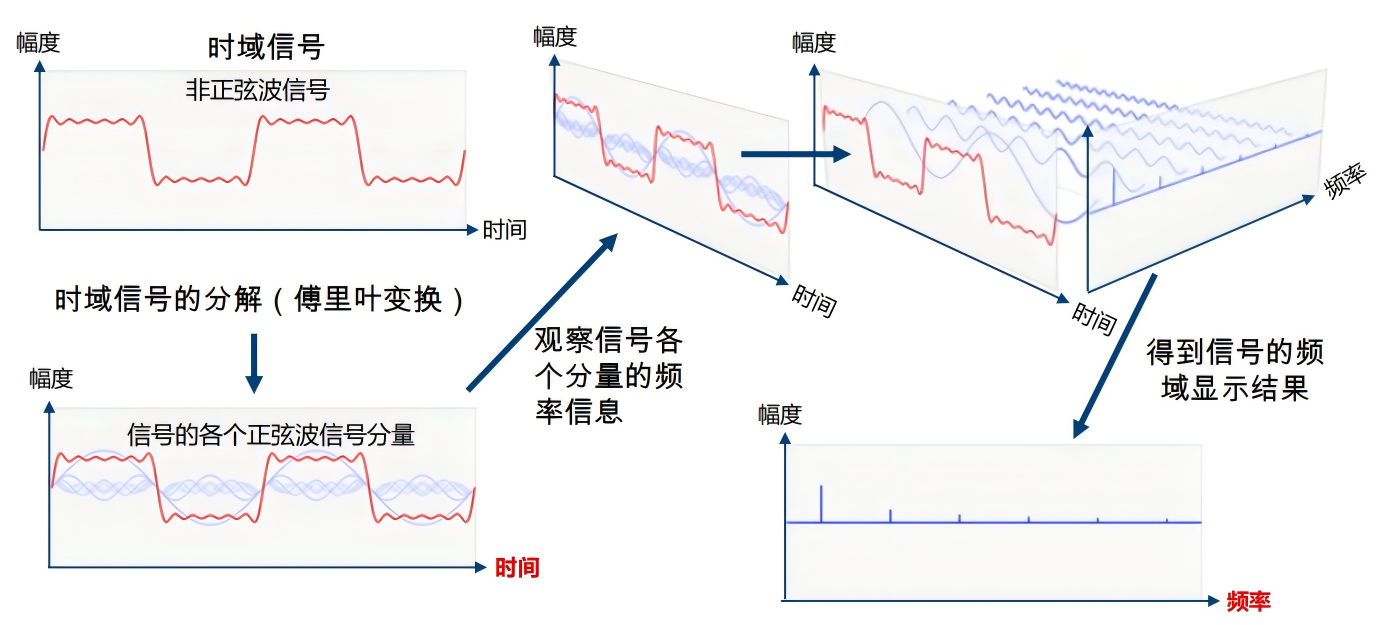
想象你在听交响乐，同时听到小提琴、大提琴、长笛…  傅里叶变换就是那个能“分离乐器”的数学工具：  

时域信号 → 我们看到的是“振幅随时间变化”的波形。

频域信号 → 傅里叶变换后看到的是“每个频率的强度”。

 

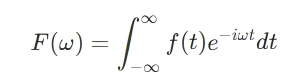核心公式

 

03

为什么伟大？它解决了什么？

信息压缩：  

JPEG图片、MP3音乐都用它压缩（保留主要频率，删掉人眼/耳不敏感的）。  

信号去噪：  

心电图EEG有噪音？滤掉高频杂波，只留心跳信号。  

通信基石：  

4G/5G/WiFi 靠它把数据“编码”到不同频率传输，互不干扰。  

图像增强：  

美颜滤镜的“磨皮”本质是去掉图像高频部分（细节皱纹），保留低频（平滑皮肤）。

 

04

延伸的应用场景

 

医学影像：MRI核磁共振靠它重建人体断层图像。

 

金融分析：股票波动分解成长期趋势 + 短期震荡。

 

天文观测：从宇宙微波背景辐射中寻找原始频率信号。

 

AI语音助手：你的“嗨 Siri”被快速转成频域特征识别。

 

地震波分析：预测石油分布、监测核试验。

 

汽车工程领域：傅里叶变换可用于诊断车辆异响问题。其原理在于：所有声音本质上都是由物体振动产生的。当车辆出现异常噪音时，往往意味着某些零部件在特定工况下发生了非预期的共振。

 

05

总结

每个系统都有一组确定的共振频率，这些频率也被称为特征频率，它是系统的固有属性，如同DNA般刻写着系统的本质特征。傅里叶变换就像一位翻译官，它能将时域中纷繁复杂的信号（随时间舞动的曲线），解码为频域中一组组永恒不变的基本元素（特定频率的正弦波）。