将从目标和问题的角度去讨论每种误差度量的有效性

模型的好坏和优劣都是基于一定的角度做出的相对判断，在这篇文章中，我们将从目标和问题的角度去讨论每种误差度量的有效性。 当有人告诉你“中国是最好的国家”时，你问的首要问题肯定是这个陈述的基础是什么，我们是根据国家的经济状况、文化水平还是他们的卫生设施等来评估比较各个国家的呢？ 类似地，每个机器学习模型都用到了不同的数据集来有针对性的解决不同目标的问题，因此，在选择合适的度量之前，要深刻理解上下文。

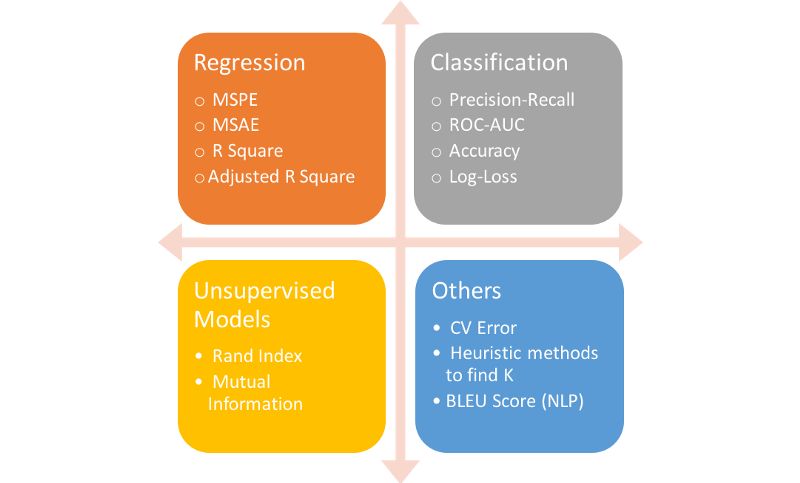
图 各种机器学习模型常用的度量标准

回归度量指标

大多数的博客更多都关注模型的精度、召回率、AUC(Area under curve，ROC曲线下区域面积)等分类指标。这里想稍稍改变一下，让我们来探索各种更多的指标，包括在回归问题中使用的指标。MAE和RMSE是关于连续变量的两个最普遍的度量标准。

首先，我们看看最流行RMSE，全称是Root Mean Square Error，即均方根误差，它表示预测值和观测值之间差异（称为残差）的样本标准偏差。在数学上，它是用如下这个公式计算的：

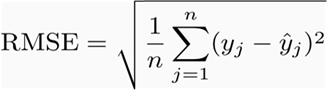
其次是MAE，全称是Mean Absolute Error，即平均绝对误差，它表示预测值和观测值之间绝对误差的平均值。MAE是一种线性分数，所有个体差异在平均值上的权重都相等，比如，10和0之间的绝对误差是5和0之间绝对误差的两倍。但这对于RMSE而言不一样，后续将进一步详细讨论。在数学上，MAE是用如下这个公式计算的：

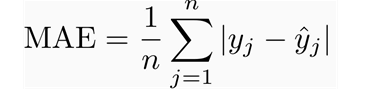
那么你应该选择哪一个？为什么这样选择呢？

首先，理解和解释MAE很容易，因为它就是对残差直接计算平均，而RMSE相比MAE，会对高的差异惩罚更多。让我们通过两个例子来理解一下：

案例1：真实值= [2,4,6,8]，预测值= [4,6,8,10]

案例2：真实值= [2,4,6,8]，预测值= [4,6,8,12]

案例1的MAE = 2.0，RMSE = 2.0

案例2的MAE = 2.5，RMSE = 2.65

从上述例子中，我们可以发现RMSE比MAE更加多地惩罚了最后一项预测值。通常，RMSE要大于或等于MAE。等于MAE的唯一情况是所有残差都*相等或都为零*，如案例1中所有的预测值与真实值之间的残差皆为2，那么MAE和RMSE值就相等。

> 尽管RMSE更复杂且偏向更高的误差，它仍然是许多模型的默认度量标准，因为用RMSE来定义损失函数是*平滑可微*的，且更容易进行数学运算。

虽然这听起来不太令人满意，但这的确是是它非常受欢迎的原因。下面我将从数学角度解释上述逻辑。首先，让我们建立一个简单的单变量线性模型：y = mx + b，在这个问题中，我们要找到最佳“m”和“b”，数据（x，y）是已知的。如果我们用RMSE来定义损失函数（J）：那么我们可以很容易地求得J对m和b的偏导，并以此来更新m和b（这是梯度下降的工作方式，这里就不过多解释它）

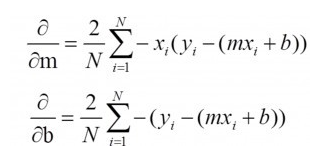
上述等式很容易就可以求解，但对MAE并不适用。然而，如果你需要一种度量标准能从直观解释的角度来比较两个模型，那么我认为MAE会是更好的选择。值得注意的是，RMSE和MAE的单位与y值相同，但R Square不是这样的。此外，RMSE和MAE的范围都是从0到无穷大。

>这里需要提及MAE和RMSE之间的一大重要区别，最小化一组数字的平方误差会得到其平均值，而最小化绝对误差则会得到其中值， 这也是为什么MAE比RMSE对离群点更有效的原因。

R Squared, R² 校正 R Squared

R² 和校正R²，常常用于说明选择的自变量对解释因变量解释拟合有多好。

在数学上，R_Squared由下式给出：

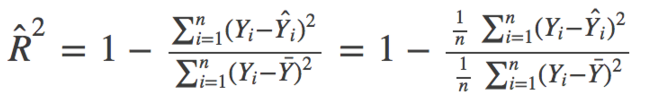
>其中，分子是MSE（残差平方的平均值），分母是Y值的方差。MSE越高，R_squared则越小，表明模型越差。

跟R²一样，校正R²也显示了自变量对因变量的解释程度，回归问题中体现于曲线的拟合优度，但是可以根据模型中的自变量个数进行调整。 它由以下公式给出：

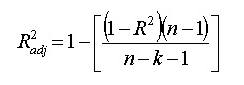
其中n表示观测值的总数，k表示预测值的数量，校正后的R²总是小于或等于R²。

为什么你应该越过R²选择校正R²？

标准的R²在使用中往往会存在一些问题，但使用校正R²就能很好地解决。因为校正R²会考虑在模型中增加附加项，使得性能改善。如果你添加有用的项，R²会增加，而如果添加了不太有用的预测变量，R²将减少。 但是，即使模型没有实际改进，R²也随着变量数量的增加而增加。下面我们用一个例子来更好地理解这一点。

这里，案例1是一个很简单的情况，我们有5个观察值（x，y）。 在案例2中，让一个变量是变量1的两倍（也就是说它与变量1完全相关）。在案例3中，我们对变量2做了轻微的干扰，使其不再与变量1完全相关。

因此，如果我们为每个案例都用简单普通的最小二乘（OLS）模型来拟合，那么从逻辑上讲，我们为案例1、案例2和案例3提供的信息是相同的，那我们的度量值相对这些模型也不会有所提高。然而，实际上R² 对于模型2和3会给出更高的值，这显然是不正确的。但是，用校正R²就可以解决这个问题，实际上对于案例2和3都是减少的。让我们给这些变量（x ，y）赋上一些值，并查看Python中获得的结果。

注意：模型1和模型2的预测值将相同，因此R²也将相同，因为它仅取决于预测值和实际值。

从上表可以看出，从案例1到案例3，尽管我们没有增加的任何附加信息，但R²仍在增加，而校正后的R²显示了正确的趋势（惩罚模型2拥有更多的变量）

对比校正R²与RMSE

对于前面的例子，我们将看到案例1和案例2得到的RMSE结果与R²是类似的。在这种情况下，校正R²要比RMSE更好，因为它只对预测值与实际值进行比较。而且，RMSE的绝对值实际上并不能说明模型有多糟糕，它只能用于比较两个模型，但校正R²就很容易做到这一点。 例如，如果一个模型的现在R²为0.05，那么这个模型肯定很差。

但是，如果你只关心预测精度，那么RMSE是最佳选择。它计算简单，容易区分，一般是大多数模型的默认度量。

常见误区：我经常看到网上说R²的范围在0到1之间，实际上并不是这样。R²的最大值是1，但最小值可以是负无穷大。即使y的真实值为正数，模型对所有观测值的预测结果也会有高负值的情况。在这种情况下，R²将小于0。这虽然是一个不太可能的情况，但可能性依然存在。

有趣的指标

这里有一个有趣的指标，如果你对NLP感兴趣，Andrew Ng在深度学习课程中介绍了它。BLEU（Bilingual Evaluation Understudy，双语评估研究）

它主要用于衡量机器翻译相对于人类翻译的质量，它使用了精确度量的修改形式。

计算BLEU分数的步骤:

1. 把句子转换成单个词、两个词、三个词和四个词

2. 分别计算大小为1至4的n语法的精度

3. 取所有这些精度值的加权平均的指数

4.将其与简短的惩罚项相乘（稍后将解释）

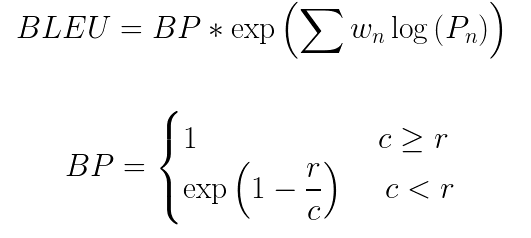
这里BP是简短的惩罚项，r和c分别是参考翻译和候选翻译中的词的数量，w 表示权重，P表示精度值

例：

参考：The cat is sitting on the mat 

机器翻译1：On the mat is a cat 

机器翻译2：There is cat sitting cat

我们来比较一下上面两个翻译的BLEU得分。

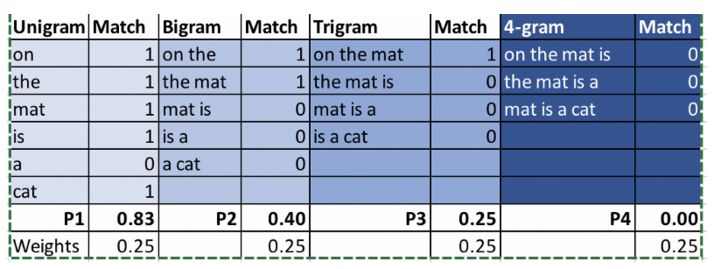
最终结果：BLEU（MT1）= 0.454，BLEU（MT2）= 0.59

为什么要引入简洁的惩罚项？

引入的惩罚项会惩罚那些短于参考翻译的候选翻译。例如，如果上述候选翻译的参考翻译是“The cat”，那么它对于单个词和两个词将具有很高的精度，因为两个单词都以相同的顺序出现在参考翻译中。但是，长度太短的话，实际上并不能很好的反映参考翻译的含义。有了这个简短的惩罚，候选翻译必须在长度、相同单词和单词顺序方面与参考翻译相匹配才能获得高分。

希望通过这篇文章的介绍，我们能理解不同度量间的差异，并能为机器学习选择合适的模型度量，评价建模效果的好坏，并指导模型的优化。