

一种新的GAN(对抗网络生成)训练方法
电子说
描述
微软研究人员在ICLR 2018发表了一种新的GAN(对抗网络生成)训练方法,boundary-seeking GAN(BGAN),可基于离散值训练GAN,并提高了GAN训练的稳定性。
对抗生成网络
首先,让我们温习一下GAN(对抗生成网络)的概念。简单来说,GAN是要生成“以假乱真”的样本。这个“以假乱真”,用形式化的语言来说,就是假定我们有一个模型G(生成网络),该模型的参数为θ,我们要找到最优的参数θ,使得模型G生成的样本的概率分布Qθ与真实数据的概率分布P尽可能接近。即:
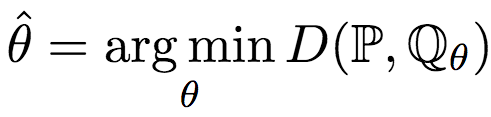
其中,D(P, Qθ)为P与Qθ差异的测度。
GAN的主要思路,是通过引入另一个模型D(判别网络),该模型的参数为φ,然后定义一个价值函数(value function),找到最优的参数φ,最大化这一价值函数。比如,最初的GAN(由Goodfellow等人在2014年提出),定义的价值函数为:
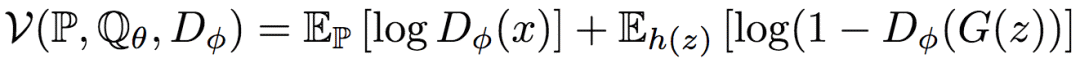
其中,Dφ为一个使用sigmoid激活输出的神经网络,也就是一个二元分类器。价值函数的第一项对应真实样本,第二项对应生成样本。根据公式,D将越多的真实样本归类为真(1),同时将越多的生成样本归类为假(0),D的价值函数的值就越高。
GAN的精髓就在于让生成网络G和判别网络D彼此对抗,在对抗中提升各自的水平。形式化地说,GAN求解以下优化问题:
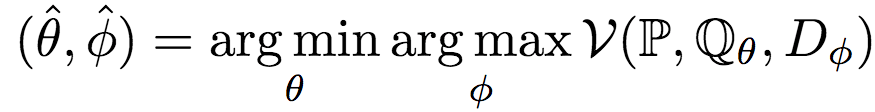
如果你熟悉Jensen-Shannon散度的话,你也许已经发现了,之前提到的最初的GAN的价值函数就是一个经过拉伸和平移的Jensen-Shannon散度:2 * DJSD(P||Qθ) - log 4. 除了这一Jensen-Shannon散度的变形外,我们还可以使用其他测度衡量分布间的距离,Nowozin等人在2016年提出的f-GAN,就将GAN的概念推广至所有f-散度,例如:
Jensen-Shannon
Kullback–Leibler
Pearson χ2
平方Hellinger
当然,实际训练GAN时,由于直接计算这些f-散度比较困难,往往采用近似的方法计算。
GAN的缺陷
GAN有两大著名的缺陷:难以处理离散数据,难以训练。
GAN难以处理离散数据
为了基于反向传播和随机梯度下降之类的方法训练网络,GAN要求价值函数在生成网络的参数θ上完全可微。这使得GAN难以生成离散数据。
假设一下,我们给生成网络加上一个阶跃函数(step function),使其输出离散值。这个阶跃函数的梯度几乎处处为0,这就使GAN无法训练了。
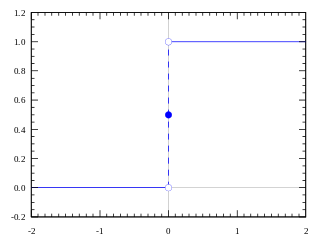
GAN难以训练
从直觉上说,训练判别网络比训练生成网络要容易得多,因为识别真假样本通常比伪造真实样本容易。所以,一旦判别网络训练过头了,能力过强,生成网络再怎么努力,也无法提高,换句话说,梯度消失了。
另一方面,如果判别网络能力太差,胡乱分辨真假,甚至把真的误认为假的,假的误认为真的,那生成网络就会很不稳定,会努力学习让生成的样本更假——因为弱智的判别网络会把某些假样本当成真样本,却把另一些真样本当成假样本。
还有一个问题,如果生成网络凑巧在生成某类真样本上特别得心应手,或者,判别网络对某类样本的辨别能力相对较差,那么生成网络会扬长避短,尽量多生成这类样本,以增大骗过判别网络的概率,这就导致了生成样本的多样性不足。
所以,判别网络需要训练得恰到好处才可以,这个火候非常难以控制。
强化学习和BGAN
那么,该如何避免GAN的缺陷呢?
我们先考虑离散值的情况。之所以GAN不支持生成离散值,是因为生成离散值导致价值函数(也就是GAN优化的目标)不再处处可微了。那么,如果我们能对GAN的目标做一些手脚,使得它既处处可微,又能衡量离散生成值的质量,是不是可以让GAN支持离散值呢?
关键在于,我们应该做什么样的改动?关于这个问题,可以从强化学习中得到灵感。实际上,GAN和强化学习很像,生成网络类似强化学习中的智能体,而骗过判别网络类似强化学习中的奖励,价值函数则是强化学习中也有的概念。而强化学习除了可以根据价值函数进行外,还可以根据策略梯度(policy gradient)进行。根据价值函数进行学习时,基于价值函数的值调整策略,迭代计算价值函数,价值函数最优,意味着当前策略是最优的。而根据策略梯度进行时,直接学习策略,通过迭代计算策略梯度,调整策略,取得最大期望回报。
咦?这个策略梯度看起来很不错呀。引入策略梯度解决了离散值导致价值函数不是处处可微的问题。更妙的是,在强化学习中,基于策略梯度学习,有时能取得比基于值函数学习更稳定、更好的效果。类似地,引入策略梯度后GAN不再直接根据是否骗过判别网络调整生成网络,而是间接基于判别网络的评价计算目标,可以提高训练的稳定度。
BGAN(boundary-seeking GAN)的思路正是如此。
BGAN论文的作者首先证明了目标密度函数p(x)等于(∂f/∂T)(T(x))qθ(x)。其中,f为生成f-散度的函数,f*为f的凸共轭函数。
令w(x) = (∂f/∂T)(T*(x)),则上式可以改写为:
p(x) = (w*(x))qθ(x)
这样改写后,很明显了,这可以看成一个重要性采样(importance sampling)问题。(重要性采样是强化学习中推导策略梯度的常用方法。)相应地,w*(x)为最优重要性权重(importance weight)。
类似地,令w(x) = (∂f*/∂T)(T(x)),我们可以得到f-散度的重要性权重估计:
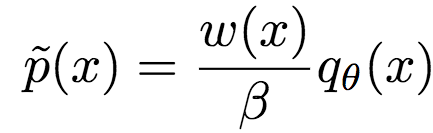
其中,β为分区函数:
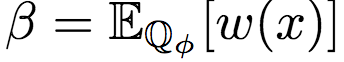
使用重要性权重作为奖励信号,可以得到基于KL散度的策略梯度:
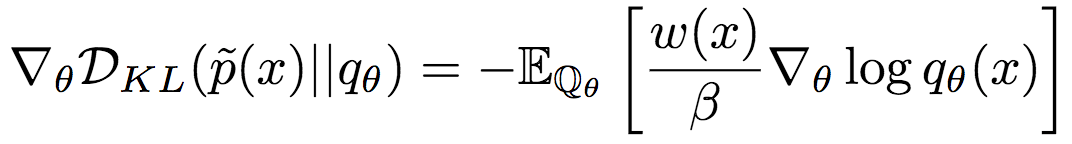
然而,由于这一策略梯度需要估计分区函数β(比如,使用蒙特卡洛法),因此,方差通常会比较大。因此,论文作者基于归一化的重要性权重降低了方差。
令
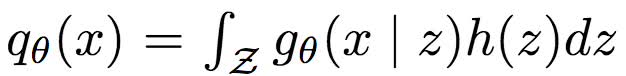
其中,gθ(x | z): Z -> [0, 1]d为条件密度,h(z)为z的先验。
令分区函数
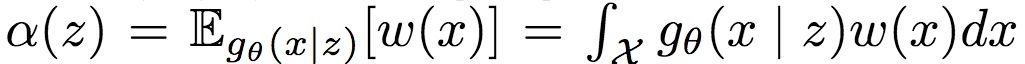
则归一化的条件权重可定义为
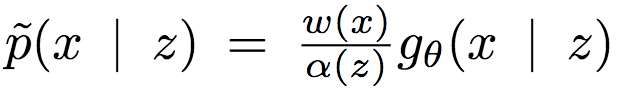
由此,可以得到期望条件KL散度:
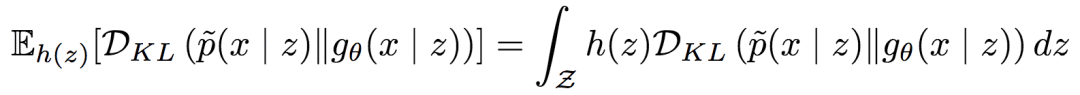
令x(m) ~ gθ(x | z)为取自先验的样本,又令
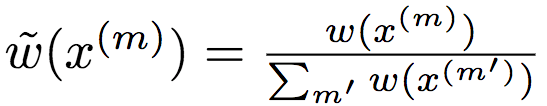
为使用蒙特卡洛估计的归一化重要性权重,则期望条件KL散度的梯度为:
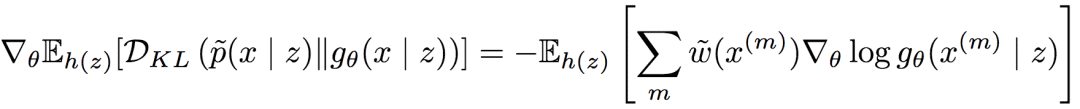
如此,论文作者成功降低了梯度的方差。
此外,如果考虑逆KL散度的梯度,则我们有:
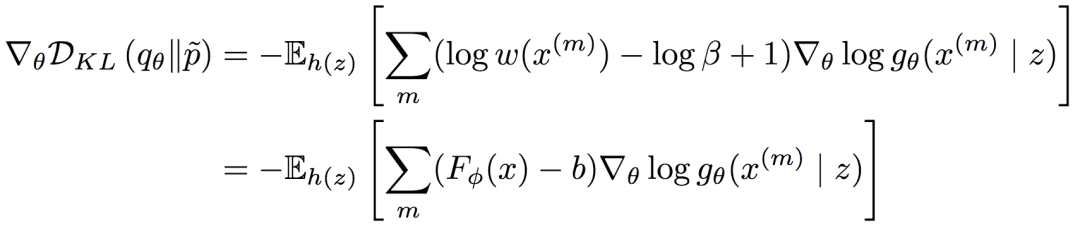
上式中,静态网络的输出Fφ(x)可以视为奖励(reward),b可以视为基线(baseline)。因此,论文作者将其称为基于强化的BGAN。
试验
离散
为了验证BGAN在离散设定下的表现,论文作者首先试验了在CIFAR-10上训练一个分类器。结果表明,搭配不同f-散度的基于重要性取样、强化的BGAN均取得了接近基线(交叉熵)的表现,大大超越了WGAN(权重裁剪)的表现。
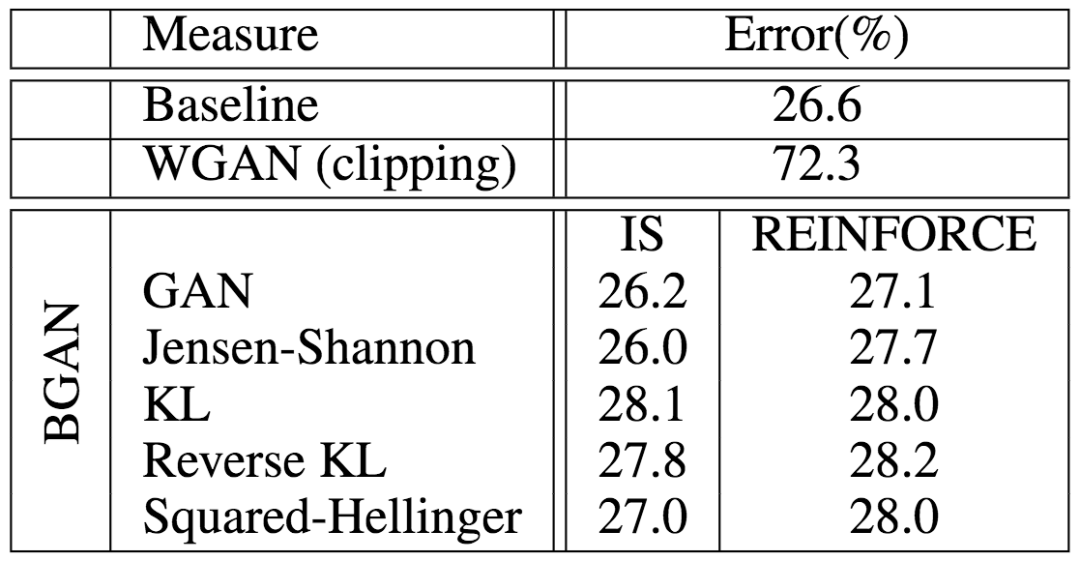
在MNIST上的试验表明,BGAN可以生成稳定、逼真的手写数字:
在MNIST上与WGAN-GP(梯度惩罚)的比较显示,采用多种距离衡量,包括Wasserstein距离,BGAN都取得了更优的表现:
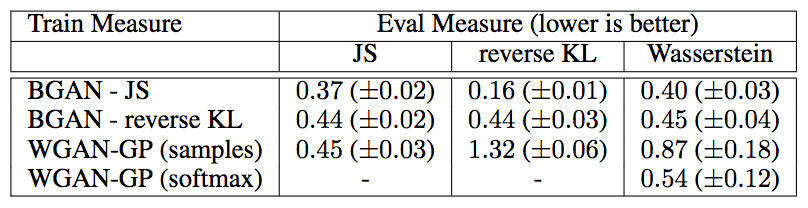
在quantized版本的CelebA数据集上的表现:
左为降采样至32x32的原图,右为BGAN生成的图片
下为随机选取的在1-billion word数据集上训练的BGAN上生成的文本的3个样本:

虽然这个效果还比不上当前最先进的基于RNN的模型,但此前尚无基于GAN训练离散值的模型能实现如此效果。
连续
论文作者试验了BGAN在CelebA、ImageNet、LSUN数据集上的表现,均能生成逼真的图像:
在CIFAR-10与原始GAN、使用代理损失(proxy loss)的DCGAN的比较表明,BGAN的表现和训练稳定性都是最优的:
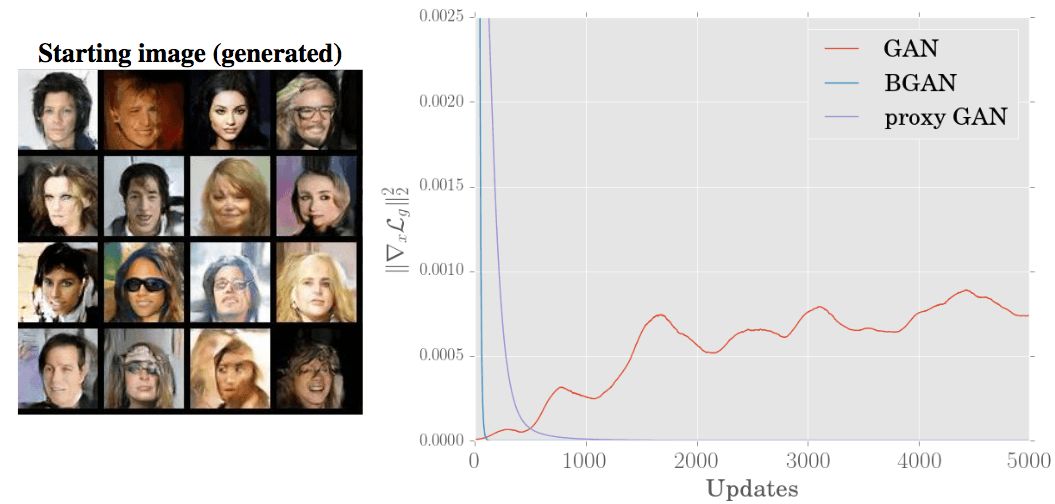
-
图像生成对抗生成网络gan_GAN生成汽车图像 精选资料推荐2021-08-31 0
-
一种基于机器学习的建筑物分割掩模自动正则化和多边形化方法2021-09-01 0
-
优化神经网络训练方法有哪些?2022-09-06 0
-
研究人员提出一种基于哈希的二值网络训练方法 比当前方法的精度提高了3%2018-02-08 5285
-
如何使用双鉴别网络进行生成对抗网络图像修复方法的说明2018-12-24 833
-
必读!生成对抗网络GAN论文TOP 102019-03-20 6662
-
生成对抗网络GAN论文TOP 10,帮助你理解最先进技术的基础2019-03-20 8971
-
一种利用生成式对抗网络的超分辨率重建算法2021-03-22 839
-
一种侧重于学习情感特征的预训练方法2021-04-13 725
-
GAN图像对抗样本生成方法研究综述2021-04-28 809
-
基于生成式对抗网络的图像补全方法2021-05-19 838
-
生成式对抗网络应用及研究综述2021-06-09 733
-
一种基于生成对抗网络的无人机图像去雾算法2022-03-10 1751
-
「自行科技」一文了解生成式对抗网络GAN2022-09-16 4295
全部0条评论

快来发表一下你的评论吧 !

