连续时间信号频域周期信号傅里叶级数和非周期信号傅里叶变换的分析

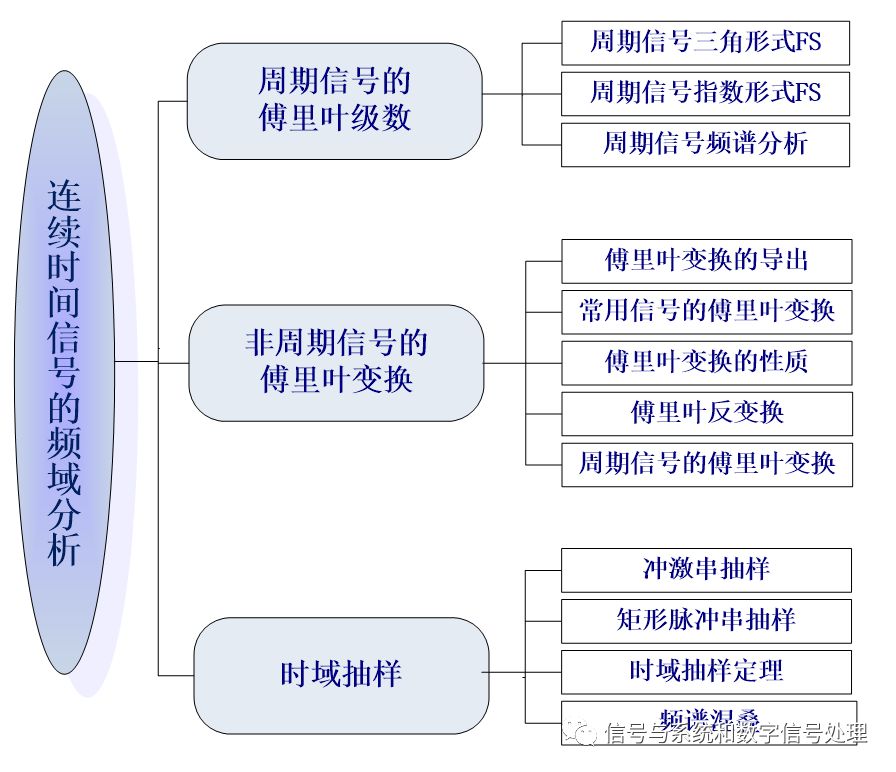
连续时间信号的频域分析，是本课程最为重要的内容之一，也是考试的重点。包括三方面内容：周期信号的傅里叶级数、非周期信号的傅里叶变换、时域抽样。具体内容如下图所示。

本文包括前面两部分：周期信号的傅里叶级数、非周期信号的傅里叶变换。

说在前头：

借助傅里叶级数这块敲门砖，我们就可以迈进频域分析的世界。但是很不幸，傅里叶级数稍显繁琐的表示形式和推导过程，使很多人望而生畏，打击了学好本课程的自信心，越学越不想学，甚至于放弃。所以，我要求大家在学习或复习傅里叶级数这部分内容的时候，要练就一颗火眼金睛，要透过繁琐的数学推导和计算，看到它背后隐藏的物理意义。特别是到傅里叶变换这部分，会出现很多神奇而美妙的结论，就好比闪闪发光的珠宝，吸引大家学好信号与系统。

一、周期信号的傅里叶级数（CTFS）

“周期信号的傅里叶级数”是打开“频域分析”大门的敲门砖，是连接时域和频域的桥梁。

主要内容包括：

1、三角形式的FS和指数形式的FS

下图给出了三角形式和指数形式的FS展开式及系数求解公式。

三角形式的FS与指数形式的FS的根本不同之处在于下面这个式子：

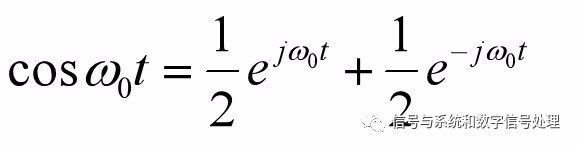
指数形式傅氏级数中有负频率项，只是表达形式的问题，并不表示真正存在以负频率进行振荡的分量，负频率项与相应的正的频率项合起来才代表一个振荡分量。

需要掌握：

第一，两种形式的正交信号集的特点；

第二，两种形式的FS的展开式的表达式及系数求解（重点）。

根据周期信号时域表达式的不同，求解方法分为两种：

第一种，当信号直接写成几个正余弦函数之和的形式时，直接与FS展开式的标准形式对比，得出FS系数，例如：

第二种，一般的周期信号，则需要利用系数求解公式进行积分运算。例如周期矩形脉冲信号的FS。教材上一般都有这道例题，这里不再重复。

2、周期信号的频谱分析

这里是本课程首次给出“频谱”的概念。用频谱来描述信号，大家一定要接受并掌握这种描述信号的新形式，理清时频对应关系，为后续课程的学习打下基础。

第一，掌握频谱的概念。衍生出来的“幅度谱”、“相位谱”、“单边谱”、“双边谱”等名词。

再从做题的角度总结一下，如下图。

第二，周期信号频谱的特点：离散性、谐波性、收敛性

第三，周期信号时域参数与频谱特性的关系

以周期矩形脉冲信号为例来分析。如下图。

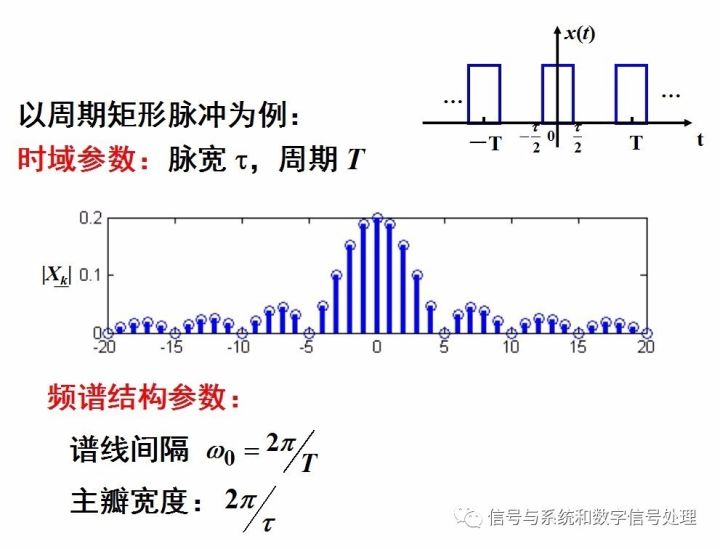
得到以下结论：

第四，时域波形对称特点与傅里叶系数的关系

如果时域波形有某种对称的特点，它的傅里叶级数会表现出一些特殊性，如下图所示。

这种特殊性，在求解一些周期信号的傅里叶级数系数时，如果运用得当，可以简化计算。

二、非周期信号的傅里叶变换（CTFT）

傅里叶变换是重点中的重点。包括以下几个方面的内容：

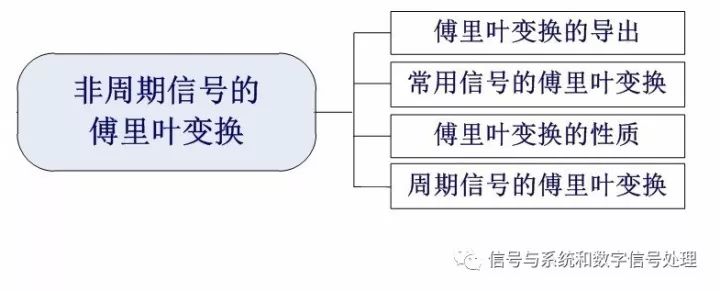
1、傅里叶变换的导出

如下图所示。 

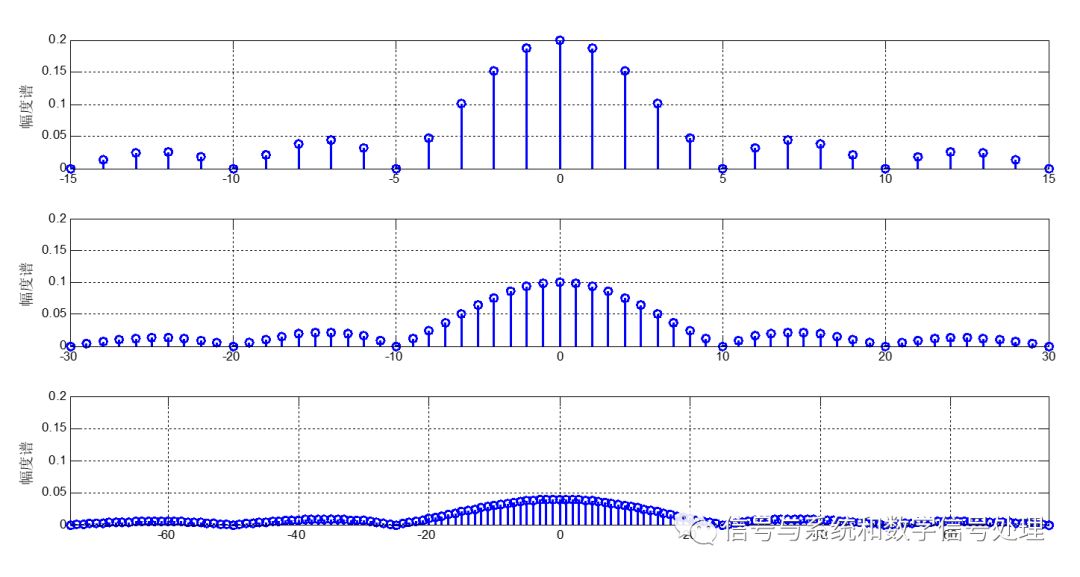
周期T→无穷大，谱线间隔→无穷小，离散谱→连续谱，但同时，谱线幅度→无穷小，此时，用FS表示频谱就不合适了。我们注意到，虽然谱线幅度趋于无穷小，但相对大小依然有区别。

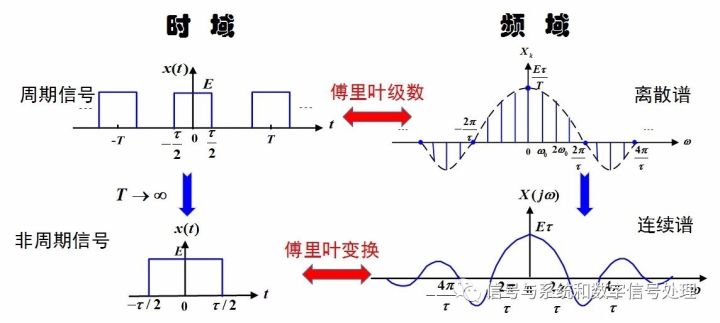
借助物理上的“密度”的概念，质量/体积=密度。导出非周期信号的傅里叶变换X(jw),它的意义是单位频带上的频谱值，称为“频谱密度函数”。

2、常用信号的傅里叶变换

冲激信号、阶跃信号、符号函数、直流信号、正弦信号、余弦信号、单边指数衰减信号、双边指数衰减信号、门函数（矩形脉冲信号）、钟形脉冲信号（高斯脉冲）、升余弦脉冲信号、sinc函数等等。以及它们的各阶导数和微分。

这些常用信号，有普通信号，也有奇异信号；有满足绝对可积条件的，也有不满足绝对可积条件的。它们的傅里叶变换的求解，分为三种情况：

第一种，直接利用定义式求解；第二种，利用已有的变换对和性质求解；第三种，特殊方法（比如阶跃信号u(t)、符号函数等）。

有些要记住、有些（比如双边指数信号、钟形脉冲、升余弦脉冲等）要能推导出来。

3、傅里叶变换的性质

利用傅里叶变换这个工具，我们可以从信号的时域描述（以时间t为自变量的函数x(t)）得到它的频域描述（X(jw)），反之亦然。傅里叶变换的性质就是研究这两个域——时域和频域之间的对应关系，什么对应关系呢？我们可以用两句话来总结，第一句话，一个域中的某些特性在另外一个域中对应什么特性？第二句话，一个域中的某种运算在另外一个域中发生什么变化？具体来说，哪些特性、哪些运算呢？比如，奇偶对称特性、展缩运算、平移、积分/微分等等。

任何一本教材上，都有傅里叶变换性质的列表，这里不面面俱到。重点讲以下几个：

展缩特性

矩形脉冲信号的傅里叶变换对能特别直观地展现展缩性质。

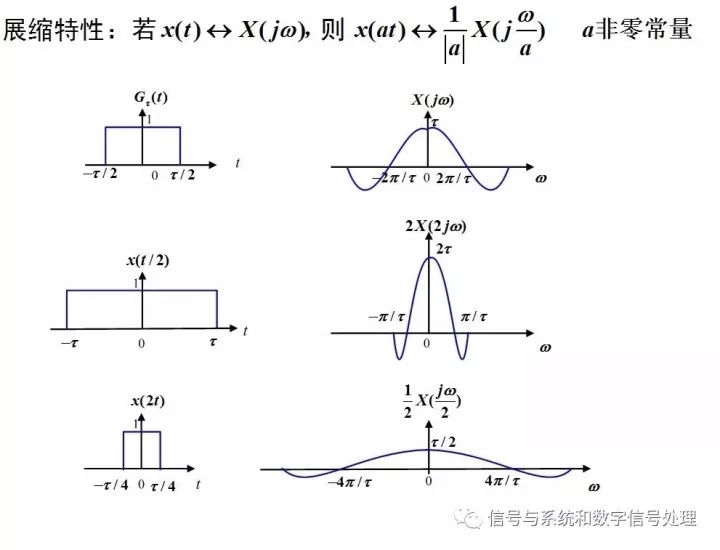
矩形脉冲的脉宽增大，时域上，非零值的时间范围增加；频域上，频谱更集中在频率原点附近。即“时域扩展，频谱压缩”，反之亦然。

展缩特性，从理论上证明了时域与频域的相反关系，也证明了信号的时宽带宽积等于常数的结论。通信中，若要压缩信号的持续时间，则信号的带宽就要展宽。要压缩信号的有效频带，就不得不增加信号的持续时间。

一般而言，时域有限，频谱无限，反之亦然。不存在时域和频域都有限的信号。

时移频移特性

时域平移，对应频域，幅频特性不变，相位谱产生附加的线性变化（+wt0）。所以波形的形状不变，因为各个频率分量的相对大小关系不变（对应幅度谱不变）、在时间轴上的相对位置关系也不变（对应相位增加一个wt0，和w成线性关系）。

频移呢，频谱的搬移是通信系统中应用广泛的技术，例如调制、解调、变频等，都是在频移的基础上完成的，频移特性是其理论基础。    

利用频移特性，我们可以推导出虚指数信号、正弦余弦信号的傅里叶变换。这三个信号都是不满足绝对可积条件的，其傅里叶变换中都存在冲激函数。

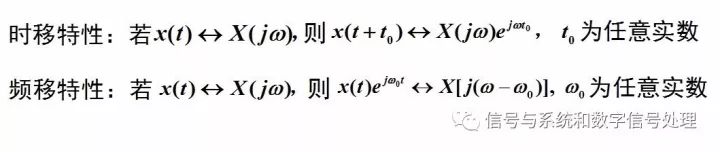
微分特性

时域微分特性和频域微分特性，可以用来求解利用公式不能或者不易求解的变换对，比如冲激偶函数、tu(t)等等。

微分特性，在系统的频域分析中很重要。因为描述连续时间系统的是微分方程，我们可以想到，傅里叶变换的方法，必将在微分方程求解（即系统响应求解）、系统分析中大有用武之地。

积分特性

积分特性也是主要用来求解一些比较复杂的信号的傅里叶变换。但是应用的时候要注意，不能把积分特性当做微分特性的倒过来，而要注意其中的直流分量，否则就会出错。

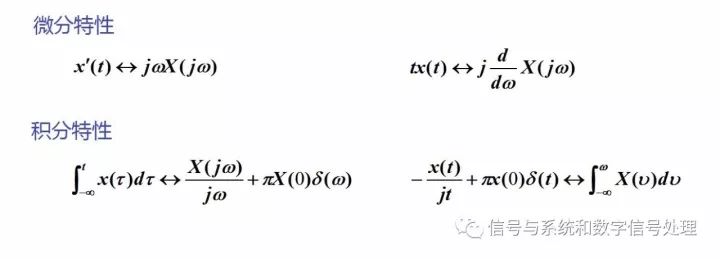
卷积特性

包括时域卷积特性和频域卷积特性，一个域相乘，另外一个域卷积，这是一个非常基本、非常重要的关系。

提供了一种计算傅里叶变换的方法，同时，也是系统的频域分析的基础。

互易对称特性

最后来说一说这个神奇而美丽的性质。

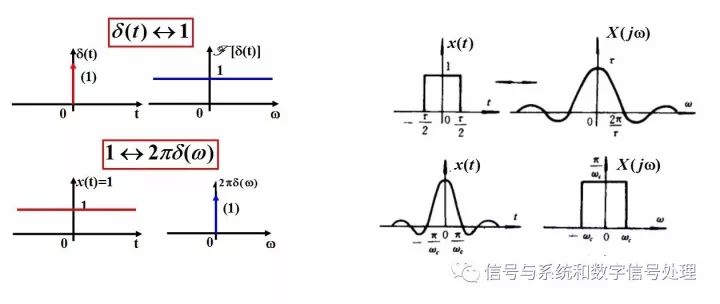
如果某个信号，在时域上有某种红色的特性，它在频域上有蓝色的特性，而另外一个信号，在时域上有这种蓝色的特性，那么它在频域上，就会以某种类似于刚才那种红色的特性表现出来。

很多变换对体现了这一点。比如，时域上的冲激信号，频谱是1；而时域上的直流1，对应频谱为2π乘上冲激函数。再比如，时域上的矩形脉冲，频谱为sinc函数；而时域的sinc信号，频谱为矩形函数。

很多傅里叶变换的性质也体现了这一点，比如时移特性与频移特性、时域微分与频域微分，等等。

最后，提一下傅里叶反变换的求解方法，有以下三种：

利用傅里叶反变换的定义式求解

利用FT的性质求解

特别注意互易对称性的应用。

部分分式展开法

部分分式展开法，不仅仅是傅里叶反变换的求解方法之一，也是后面的拉氏变换、z变换的反变换求解方法。

4、周期信号的傅里叶变换

周期信号，不满足绝对可积，如果带入到傅里叶变换的公式里，积分是不收敛的，那是不是就意味着，周期信号的傅里叶变换不存在呢？不是的。我们前面在讲解傅里叶变换的性质时，已经求解出了正余弦信号的傅里叶变换对，发现它们的傅里叶变换中有冲激函数，所以，通过引入冲激函数，不满足绝对可积条件的周期信号，也可以用傅里叶变换来表示。这样，傅里叶变换就把傅里叶级数统一起来了。

傅里叶级数和傅里叶变换之间到底是什么关系呢？用下图很容易理解二者的关系。

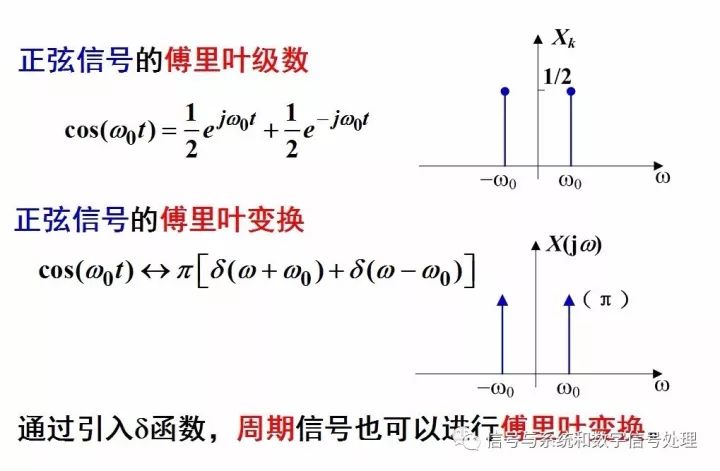
周期信号的傅里叶变换是一系列强度为2πXk，发生在谐波频率kw0上的冲激串的线性组合，仍是离散谱。

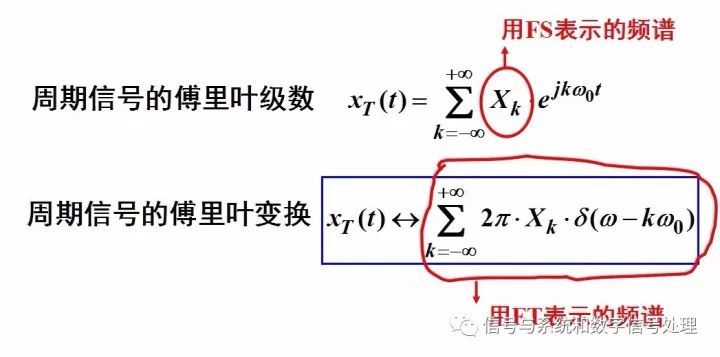
可以推导出一个非常重要、非常有趣、非常美丽的一个变换对，如下图

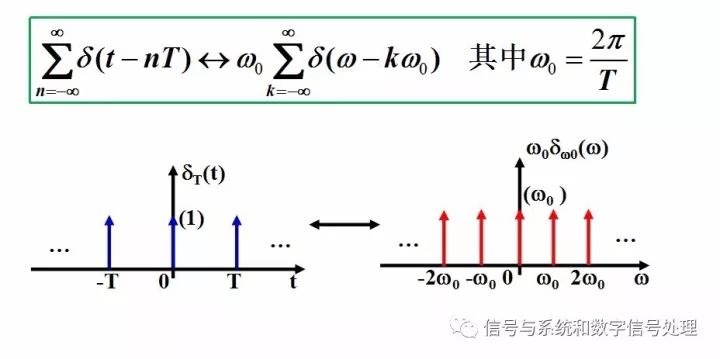
上图所示的这个变换对，会在“时域抽样”部分中发挥重要的作用。