

基于NumPy从头搭建神经网络,分步骤详细讲解
电子说
描述
编者按:和Daphne Cornelisse一起基于NumPy从头搭建神经网络,包含分步骤详细讲解,并在这一过程中介绍神经网络的基本概念。
本文将介绍创建一个三层神经网络所需的步骤。我将在求解问题的过程中,一边和你解释这一过程,一边介绍一些最重要的概念。
需要求解的问题
意大利的一个农夫的标签机出故障了:将三种不同品种的葡萄酒的标签弄混了。现在剩下178瓶酒,没人知道每瓶酒是什么品种!为了帮助这个可怜人,我们将创建一个分类器,基于葡萄酒的13个属性识别其品种。
我们的数据是有标签的(三种品种之一),这一事实意味着我们面临的是一个监督学习问题。基本上,我们想要做的是使用我们的输入数据(178瓶未分类的酒),通过神经网络,输出每瓶酒的正确标签。
我们将训练算法,使其预测每瓶酒属于哪个标签的能力越来越强。
现在是时候开始创建神经网络了!
方法
创建一个神经网络类似编写一个非常复杂的函数,或者料理一道非常困难的菜肴。刚开始,你需要考虑的原料和步骤看起来很吓人。但是,如果你把一切分解开来,一步一步地进行,会很顺利。
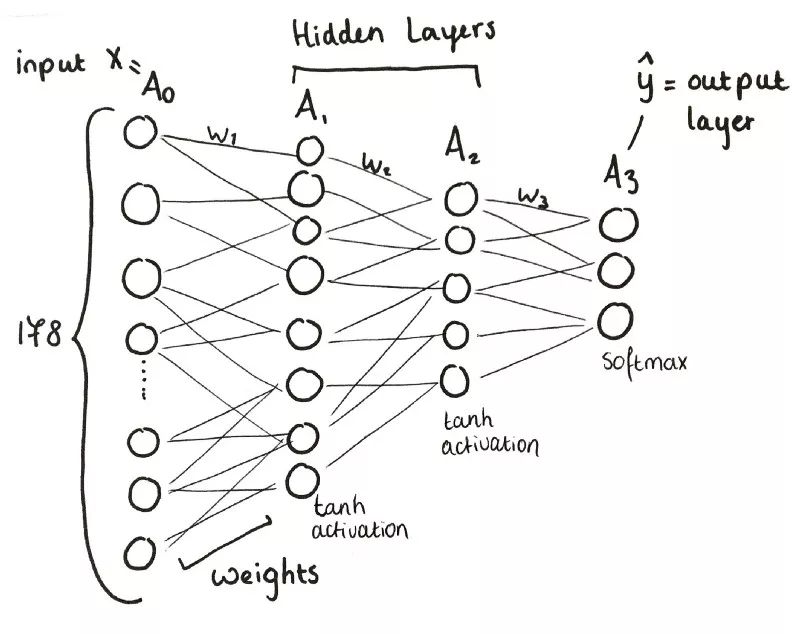
三层神经网络概览
简单来说:
输入层(x)包含178个神经元。
A1,第一层,包含8个神经元。
A2,第二层,包含5个神经元。
A3,第三层,也是输出层,包含3个神经元。
第一步:预备
导入所有需要的库(NumPy、scikit-learn、pandas)和数据集,定义x和y.
# 导入库和数据集
import pandas as pd
import numpy as np
df = pd.read_csv('../input/W1data.csv')
df.head()
# Matplotlib是一个绘图库
import matplotlib
import matplotlib.pyplot as plt
# scikit-learn是一个机器学习工具库
import sklearn
import sklearn.datasets
import sklearn.linear_model
from sklearn.preprocessing importOneHotEncoder
from sklearn.metrics import accuracy_score
第二步:初始化
在使用权重之前,我们需要初始化权重。由于我们目前还没有用于权重的值,我们使用0到1之间的随机值。
在Python中,random.seed函数生成“随机数字”。然而,随机数字并不是真随机。这些生成的数字是伪随机的,意思是,这些数字是通过非常复杂的公式生成的,看起来像是随机的。为了生成数字,公式需要之前生成的值作为输入。如果之前没有生成过数字,公式常常接受时间作为输入。
所以这里我们给生成器设置了一个种子——确保我们总是得到同样的随机数字。我们提供了一个固定值,这里我们选择了零。
np.random.seed(0)
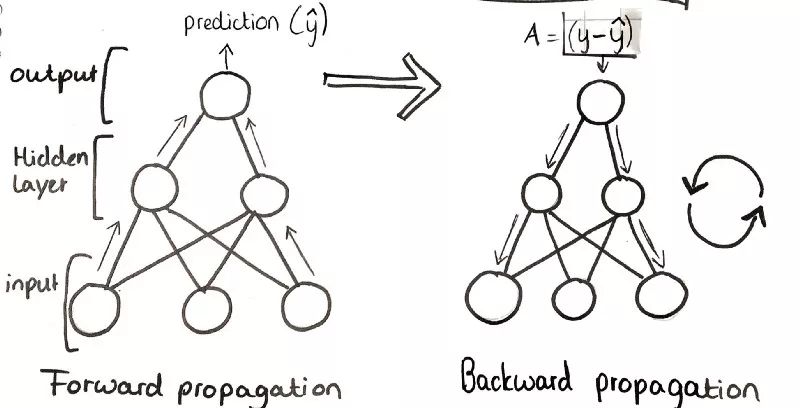
第三步:前向传播
训练一个神经网络大致可以分为两部分。首先,前向传播通过网络。也就是说,前向“步进”,并比较结果和真实值。
使用伪随机数初始化权重后,我们进行一个线性的前向步骤。我们将输入A0和随机初始化的权重的点积加上一个偏置。刚开始,我们的偏置取值为0.
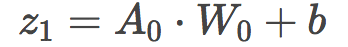
接着我们将z1(线性步骤)传给第一个激活函数。激活函数是神经网络中非常重要的部分。通过将线性输入转换为非线性输出,激活函数给我们的函数引入了非线性,使它得以表示更复杂的函数。
有许多不同种类的激活函数(这篇文章详细介绍了它们)。这一模型中,我们为两个隐藏层——A1和A2——选择了tanh激活函数,该函数的输出范围为-1到1.
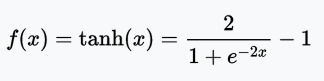
由于这是一个多类分类问题(我们有3个输出标签),我们将在输出层A3使用softmax函数,它将计算分类的概率,也就是每瓶酒属于3个分类的概率,并确保3个概率之和为1.
让z1通过激活函数,我们创建了第一个隐藏层——A1——输出值可以作为下一个线性步骤z2的输入。
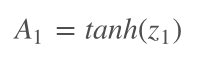
在Python中,这一步骤看起来是这样的:
# 前向传播函数
def forward_prop(model,a0):
# 加载模型参数
W1, b1, W2, b2, W3, b3 = model['W1'], model['b1'], model['W2'], model['b2'], model['W3'],model['b3']
# 第一个线性步骤
z1 = a0.dot(W1) + b1
# 让它通过第一个激活函数
a1 = np.tanh(z1)
# 第二个线性步骤
z2 = a1.dot(W2) + b2
# 让它通过第二个激活函数
a2 = np.tanh(z2)
# 第三个线性步骤
z3 = a2.dot(W3) + b3
# 第三个激活函数使用softmax
a3 = softmax(z3)
# 保存所有计算所得值
cache = {'a0':a0,'z1':z1,'a1':a1,'z2':z2,'a2':a2,'a3':a3,'z3':z3}
return cache
第四步:反向传播
正向传播之后,我们反向传播误差梯度以更新权重参数。
我们通过计算误差函数对网络权重(W)的导数,也就是梯度下降进行反向传播。
让我们通过一个类比可视化这一过程。
想象一下,你在午后到山上徒步。过了一个小时后,你有点饿了,是时候回家了。唯一的问题是天变黑了,山上还有很多树,你看不到家在何处,也搞不清楚自己在哪里。噢,你还把手机忘在家里了。
不过,你还记得你的房子在山谷中,整个区域的最低点。所以,如果你一步一步地沿着山势朝下走,直到你感觉不到任何坡度,理论上你就到家了。
所以你就小心地一步一步朝下走。现在,将山想象成损失函数,将你想象成试图找到家(即,最低点)的算法。每次你向下走一步,我们更新你的位置坐标(算法更新它的参数)。

山表示损失函数。为了得到较低的损失,算法沿着损失函数的坡度——也就是导数——下降。
当我们沿着山势朝下走的时候,我们更新位置的坐标。算法更新神经网络的权重。通过接近最小值,来接近我们的目标——最小化误差。
在现实中,梯度下降看起来是这样的:
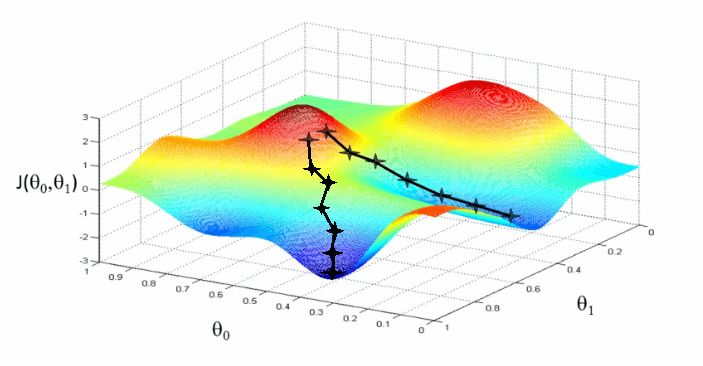
我们总是从计算损失函数的坡度(相对于线性步骤z)开始。
我们使用如下的记号:dv是损失函数对变量v的导数。
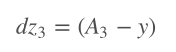
接着我们计算损失函数相对于权重和偏置的坡度。因为这是一个3层神经网络,我们将在z3,2,1、W3,2,1、b3,2,1上迭代这一过程。从输出层反向传播到输入层。
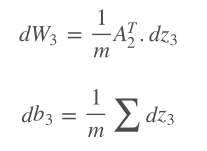
在Python中,这一过程是这样的:
# 这是反向传播函数
def backward_prop(model,cache,y):
# 从模型中加载参数
W1, b1, W2, b2, W3, b3 = model['W1'], model['b1'], model['W2'], model['b2'],model['W3'],model['b3']
# 加载前向传播结果
a0,a1, a2,a3 = cache['a0'],cache['a1'],cache['a2'],cache['a3']
# 获取样本数
m = y.shape[0]
# 计算损失函数对输出的导数
dz3 = loss_derivative(y=y,y_hat=a3)
# 计算损失函数对第二层权重的导数
dW3 = 1/m*(a2.T).dot(dz3)
# 计算损失函数对第二层偏置的导数
db3 = 1/m*np.sum(dz3, axis=0)
# 计算损失函数对第一层的导数
dz2 = np.multiply(dz3.dot(W3.T) ,tanh_derivative(a2))
# 计算损失函数对第一层权重的导数
dW2 = 1/m*np.dot(a1.T, dz2)
# 计算损失函数对第一层偏置的导数
db2 = 1/m*np.sum(dz2, axis=0)
dz1 = np.multiply(dz2.dot(W2.T),tanh_derivative(a1))
dW1 = 1/m*np.dot(a0.T,dz1)
db1 = 1/m*np.sum(dz1,axis=0)
# 储存梯度
grads = {'dW3':dW3, 'db3':db3, 'dW2':dW2,'db2':db2,'dW1':dW1,'db1':db1}
return grads
第五步:训练阶段
为了达到可以给我们想要的输出(三种葡萄酒品种)的最佳权重和偏置,我们需要训练我们的神经网络。
我认为这非常符合直觉。生活中几乎每件事情,你都需要训练和练习许多次,才可能擅长做这件事。类似地,神经网络需要经历许多个epoch或迭代,才可能给出精确的预测。
当你学习任何事情时,比如阅读一本书,你都有一个特定的节奏。节奏不应该太慢,否则要花好些年才能读完一本书。但节奏也不能太快,否则你可能会错过书中非常重要的内容。
同理,你需要为模型指定一个“学习率”。学习率是更新参数时乘上的系数。它决定参数的变动有多快。如果学习率很低,训练将花更多时间。然而,如果学习率太高,我们可能错过极小值。
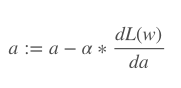
:= 意味着这是一个定义,不是一个等式,或证明的结论。
a是学习率(称为alpha)。
dL(w)是总损失对权重w的导数。
da是alpha的导数。
我们在一些试验之后将学习率定为0.07.
# 这是我们最后返回的东西
model = initialise_parameters(nn_input_dim=13, nn_hdim= 5, nn_output_dim= 3)
model = train(model,X,y,learning_rate=0.07,epochs=4500,print_loss=True)
plt.plot(losses)
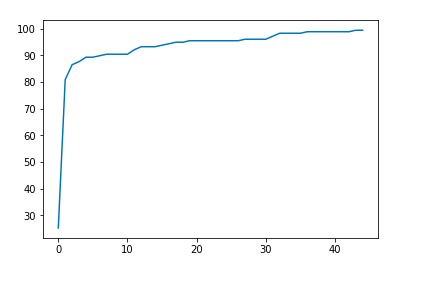
最后,这是我们的图像。你可以绘制精确度和/或损失以得到预测表现的图像。4500个epoch之后,我们的算法达到了99.4382022472 %的精确度。
简短总结
我们从将数据传入神经网络开始,并对输入数据逐层进行一些矩阵操作。在三个网络层的每一层上,我们将输入和权重的点积加上偏置,接着将输出传给选择的激活函数。
激活函数的输出接着作为下一层的输入,并重复前面的过程。这一过程迭代三次,因为我们有三个网络层。我们的最终输出是哪瓶酒属于哪个品种的预测,这是前向传播过程的终点。
我们接着计算预测和期望输出之间的差距,并在反向传播过程中使用这一误差值。
在反向传播过程中,我们将误差通过某种数学方式在网络上进行反方向传播。我们从错误中学习。
通过计算我们在前向传播过程中使用的函数的导数,我们试图发现我们应该给权重什么值,以做出尽可能好的预测。基本上,我们想要知道权重值和我们所得结果的误差之间的关系。
在许多个epoch或迭代之后,神经网络的参数逐渐适配我们的数据集,学习给出更精确的预测。
本文基于Bletchley Machine Learning训练营第一周的挑战。在这一训练营中,我们每周讨论一个不同的主题,并完成一项挑战(需要真正理解讨论的材料才能做到)。
-
labview BP神经网络的实现2017-02-22 0
-
【PYNQ-Z2试用体验】神经网络基础知识2019-03-03 0
-
【PYNQ-Z2试用体验】基于PYNQ-Z2的神经网络图形识别[结项]2019-03-18 0
-
使用keras搭建神经网络实现基于深度学习算法的股票价格预测2022-02-08 0
-
基于Numpy实现同态加密神经网络2018-03-27 7965
-
基于Numpy实现神经网络:反向传播2018-04-01 5166
-
如何使用numpy搭建一个卷积神经网络详细方法和程序概述2018-10-20 6077
-
如何使用Numpy搭建神经网络2019-05-18 3606
-
用Python从头实现一个神经网络来理解神经网络的原理12023-02-27 703
-
用Python从头实现一个神经网络来理解神经网络的原理22023-02-27 630
-
用Python从头实现一个神经网络来理解神经网络的原理32023-02-27 738
-
用Python从头实现一个神经网络来理解神经网络的原理42023-02-27 698
-
卷积神经网络层级结构 卷积神经网络的卷积层讲解2023-08-21 8938
-
卷积神经网络模型搭建2023-08-21 969
-
使用NumPy实现前馈神经网络2024-07-11 1647
全部0条评论

快来发表一下你的评论吧 !

