

贝兹孔波导定向耦合器的实现详细教程
模拟技术
描述
波导耦合器由于低插损,高功率,高定向性微波通信,测试测量等场合有大量的使用。同时波导耦合器由于是三维结构,耦合方式多种多样(宽边/窄边/多路/平行/交叉耦合),其中应用非常广泛的一种结构是贝兹孔耦合器(也称小孔耦合器),贝兹多孔耦合器遵循分支线电桥原理。这里介绍一个Vband(65G~75G)的多孔耦合器设计思路。
1、分支线电桥的原理分析
分支线电桥理论讲解比较好的书个人推荐《现代微波滤波器结构与设计》下册第15章的内容,分支线电桥作为对称的四端口网络同样适用于奇偶模分析,原理图见1所示。(详细内容参考该书15.8节)
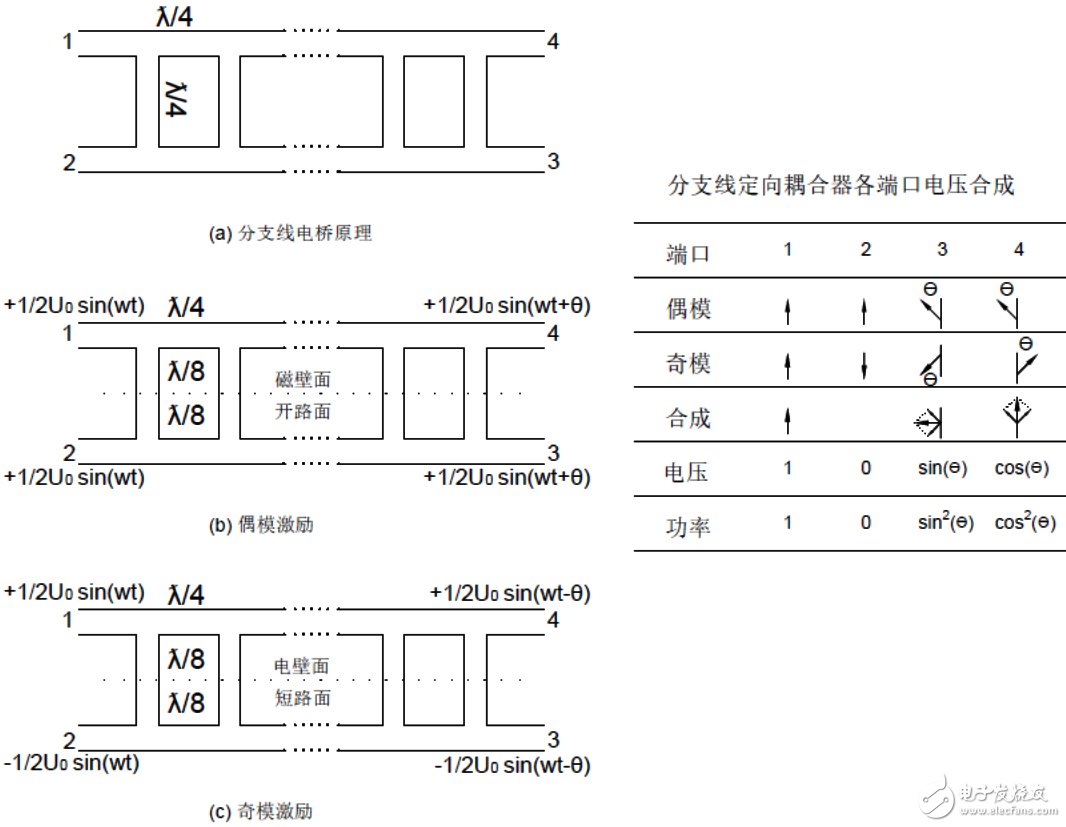
图1、分支线电桥原理分析
对于偶模激励,分支线电桥的对称面可以看作是一磁壁如图1(b)所示,取其一半分析(另一半一模一样),电路可以看成是支线为1/8波长的开路短截线,且各短截线间隔1/4波长。电压经过这样一个电路会移相θ。
同理对于奇模馈电,电路可以看成电路可以看成是支线为1/8波长的短路短截线,且各短截线间隔1/4波长。电压经过此电路会移相-θ。
第一个重要结论为:经过奇偶模叠加后的功率:
· 1口为1
· 2口为0(隔离)
· 3口为sin(θ)^2
· 4口为cos(θ)^2
· 4口和3口的输出在中心频率上相位相差90°,为90°定向耦合器。
(假如θ=45°,则电桥是一个3分贝电桥,如果θ=30°,则电桥是一个6分贝电桥,因此耦合度可以用一个角度进行表示,这里也可以融会贯通一下移相器知识)
2、分支线电桥的叠加原理
若把几个匹配的定向耦合器级联起来,则他们级联后的作用就如同一个定向耦合器一样,级联后的响应符合角度叠加原理(耦合线型耦合器也符合此原理)。例如,一个3分贝电桥是45°,我们可以用两个22.5度的电桥级联起来,一个22.5°的电桥耦合度=20*log(sin22.5)=-8.343dB.这也是8343耦合器流行的原因。
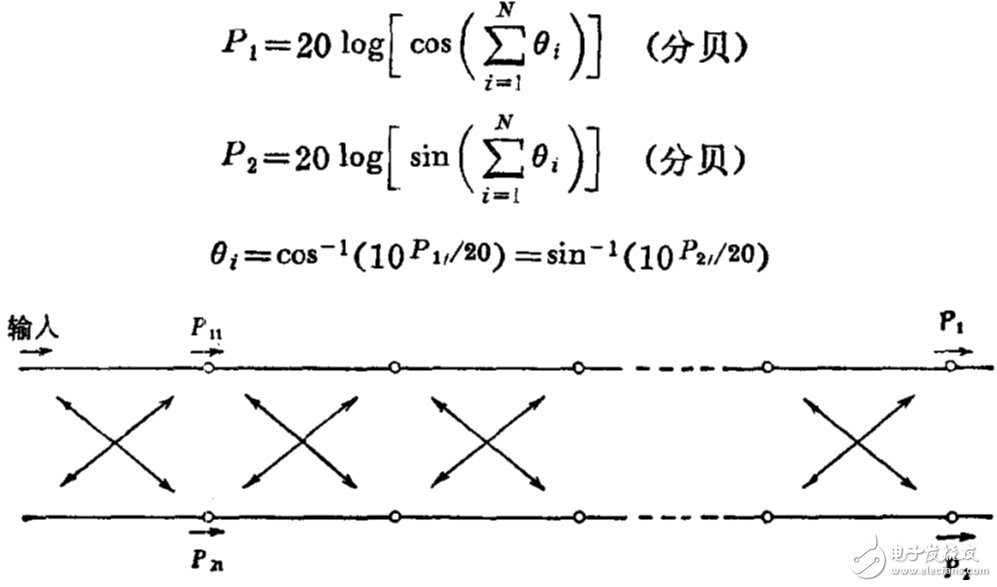
图2、电桥或耦合器叠加原理图
3、分支线电桥ADS原理仿真
小孔耦合器服从分支线电桥原理,我们在ADS中建立分支线电桥模型,获取每一级小孔的耦合度,原理图见图3,经过简单优化可以得到理想的各枝节阻抗。由于分支线电桥符合叠加原理,我们可以计算出每一节分支线提供的耦合度,那么多孔耦合器设计就变成了单孔耦合器设计。
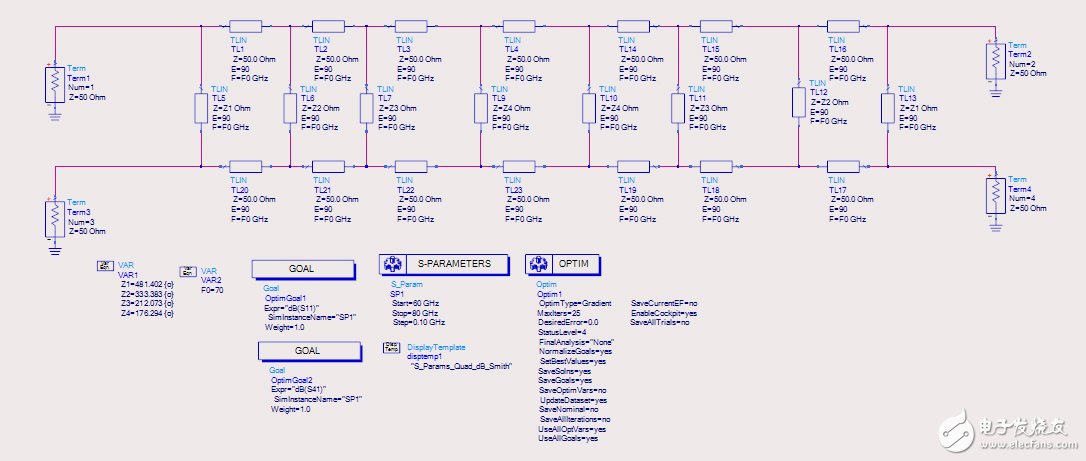
图3、ADS中分支线电桥建模
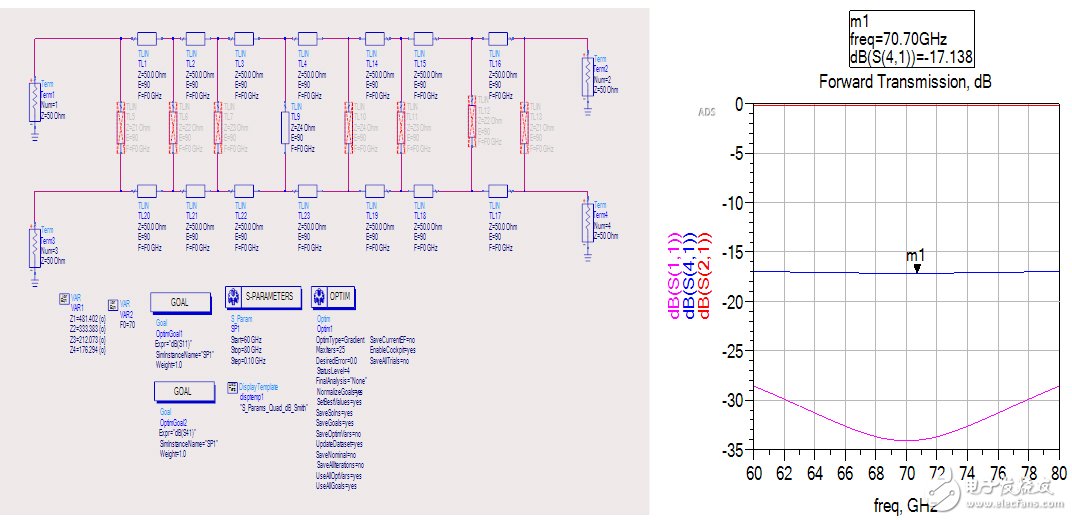
图4、单枝节耦合度确定方法
通过图4的操作,顺序使能各分枝节,可以确定每个枝节对耦合度的贡献值,这样我们就把多孔问题变成了单孔耦合问题。例如图4中第四个枝节提供了-17dB的耦合度,我们只要在三维仿真中找出一个-17dB的耦合孔即可。
4、耦合器的三维仿真
通过ADS中的原理仿真我们可以确定每一节耦合度,这样我们把多孔问题转换成了单孔问题。耦合器的三维仿真就变成了单孔耦合数据获取和多孔级联联防两个步骤。
· 单孔耦合度确定
两个平行波导只要有一个小孔就会产生耦合,耦合孔的形式结构多种多样,这里用一个双孔耦合作为实例,其他耦合形式可按照本文步骤自行感受。
在HFSS中建立图5所示的模型,两个波导间的壁厚根据机械加工的限制尽可能的薄,这里取0.4mm,通过扫描耦合孔的尺寸来获取相应耦合度。Vband的波导尺寸为:a =3.1mm,b=1.55mm,两孔间壁厚至少0.4mm,则耦合孔半径最大取0.65mm,最小取0.25mm(钻头限制)。
通过小孔直径扫描可以看到两个小孔最大可以提供-29.5dB的耦合度,远低于ADS仿真中需要的最大耦合度。(一般情况下要先评估每节耦合可以提供的最大和最小耦合量,然后在ADS中建模)通过这个步骤确定了小孔能实现耦合量的上下限,这里可以返回到ADS中重新建模仿真。(注意耦合路和直通路的相位差也要保证为90°)
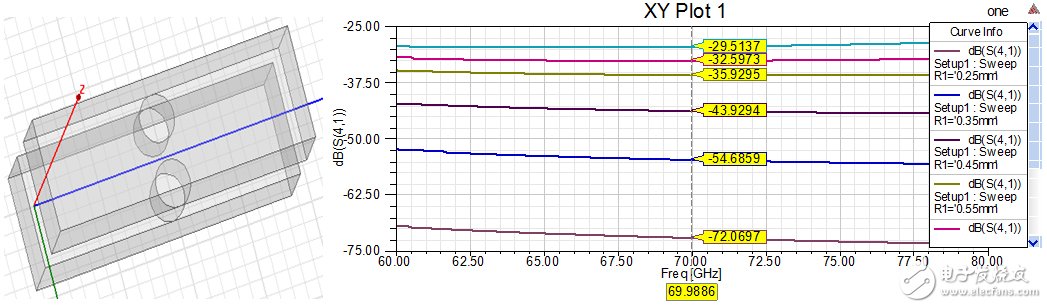
图5、HFSS中的双孔单节耦合
· 多孔耦合器三维仿真
由于小孔能提供的最大耦合量-29.5dB,耦合量非常小,这里就不返回ADS中仿真了,直接用-29.5dB的单节耦合器进行多节级联实现3dB耦合。
通过计算,-29.5°的角度是1.92°,要实现45°,可以通过45/1.92=23节去实现。在HFSS中建立23节的耦合器,每节耦合器耦合度-29.5dB,耦合孔间距1/4波长(1/4波长自行计算)。通过一次计算结果见图6所示,可以看到我们粗略估计出来的结果也是非常不错的。

图6、Vband多孔耦合器仿真结果
在实际的产品中由于存在损耗,耦合度不一定刚好-3dB合适,需要实际调试修正。
分支线电桥中各分支的耦合度越小,电桥可以做的越宽,但在ADS原理图中可以看到-20dB左右的耦合量时,分支线阻抗已经达到了200欧,这样的阻抗在微带中是非常难实现的,这也是为什么宽带的微带电桥不能使用分支线方式,同时宽带的移相器也非常难实现的原因。
-
定向耦合器的工作原理及作用是什么2023-08-18 5948
-
什么是定向耦合器?定向耦合器的作用有哪些?-科兰2023-06-16 2024
-
浅析定向耦合器的作用2023-04-03 1418
-
WCC系列交叉定向耦合器WENTEQ2022-11-16 1331
-
如何实现贝兹孔波导定向耦合器2020-10-27 1214
-
小型化大功率波导定向耦合器的研究与设计2020-04-15 1334
-
如何使用S波段实现新型宽带高功率波导定向耦合器的研究与设计2020-04-01 1311
-
定向耦合器的两种耦合方式和如何设计与制作双定向耦合器2020-03-27 3858
-
定向耦合器的网络分析方法和超宽带对称定向耦合器的设计说明2020-01-08 1768
-
如何设计硅基太赫兹波导定向耦合器及制作2019-12-23 1451
-
波导短缝耦合器的实现方式2019-07-05 2998
-
定向耦合器的应用2018-01-23 4042
-
定向耦合器的作用2010-02-07 18842
-
波导同轴定向耦合器设计2009-11-01 1356
全部0条评论

快来发表一下你的评论吧 !

