一种广义的线性回归分析模型:逻辑回归

逻辑回归又称逻辑回归分析，是一种广义的线性回归分析模型，常用于数据挖掘、疾病自动诊断、经济预测等领域。

逻辑回归是始于输出结果为实际意义的连续值的线性回归，因此与多重性线性回归分析有很多的相同之处。

逻辑回归模型

逻辑回归是一种极易理解的模型，就相当于y=f(x),表明自变量x与因变量y的关系。最常见的问题如：医生治病时的望闻问切，之后判断病人是否生病或生了什么病，其中的望闻问切就是获取自变量x，即特征数据，判断是否生病就相当于获取因变量y，及预测分类。

图1 线性回归示例

最简单的回归就是线性回归，借用Andrew NG的讲义来说，如图1.a所示，x为数据点---肿瘤的大小，y为观测值---是否有恶性肿瘤。通过构建线性回归模型，如hθ(x)所示，构建线性回归模型后，既可以根据肿瘤大小，预测是否为恶性肿瘤hθ(x)≥0.5为恶性，hθ(x)＜0.5为良性。

同时线性回归的鲁棒性很差，例如在图1.b的数据集上建立回归，因最右边噪点的存在，使回归模型在训练集上表现都很差。这主要是由于线性回归在整个实数域内敏感度一致，而分类范围，需要在[0,1]。逻辑回归就是一种减少预测范围，将预测值限定为[0,1]间的一种回归模型，其回归方程与回归曲线如图2所示。逻辑曲线在z=0时，十分敏感，在z＞＞0或z＜＜0处，都不敏感，将预测值限定为(0,1)。

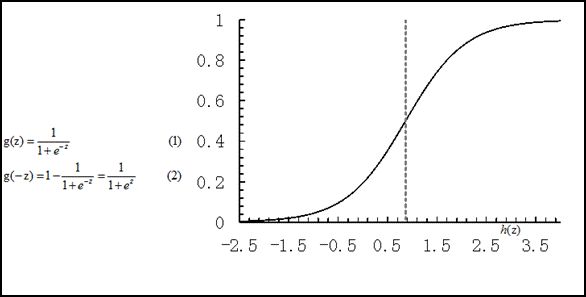
图2 逻辑方程与逻辑曲线

逻辑回归其实仅为在线性回归的基础上，套用了一个逻辑函数，但也就由于这个逻辑函数，逻辑回归成为了机器学习领域一颗耀眼的明星，更是计算广告学的核心，对于多元逻辑回归，可用如下公式似和分类，其中公式(4)的变换，将在逻辑回归模型参数估计时，化简公式带来很多益处，y={0,1}为分类结果。

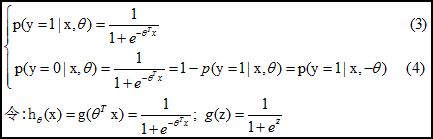
2. 判定边界

为什么逻辑回归能够解决分类问题呢？我们可以用判定边界来解释，可以理解为是用对不同类别的数据分割的边界，边界的两旁应该是不同类别的数据。

从二维直角坐标系中，举几个例子，大概是如下这三种类型：

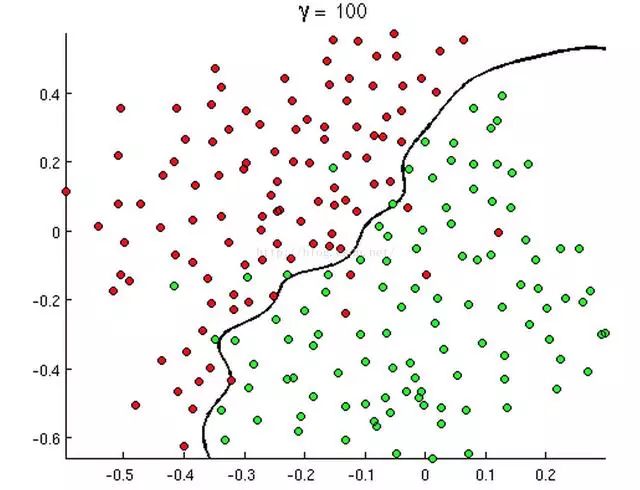
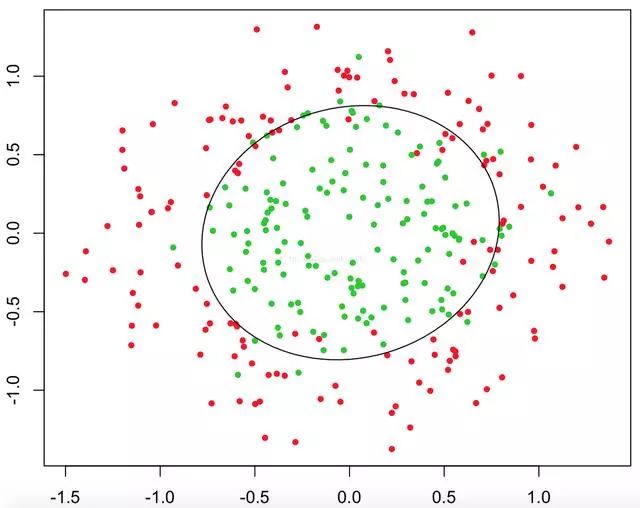
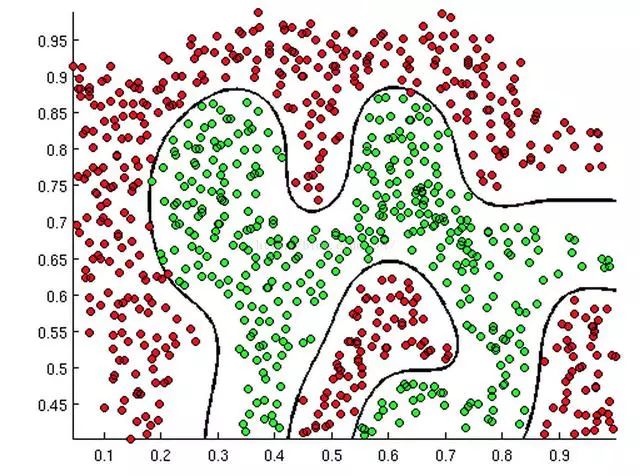
从上述三幅图中，红绿样本点为不同类别的样本，而我们划出的线，不管是直线、圆或者是曲线，都能比较好地将图中的两类样本分隔开，这就是我们所说的判定边界，那么逻辑回归是如何根据样本点来获得这些判定边界的呢？

我们依旧借用Andrew NG教授的课程中部分例子来讲述这个问题。

回到sigmoid函数，我们发现，当g(z)≥0.5时, z≥0;对于hθ(x)=g(θTX)≥0.5, 则θTX≥0, 此时意味着预估y=1;反之，当预测y = 0时，θTX<0; 所以我们认为θTX =0是一个决策边界，当它大于0或小于0时，逻辑回归模型分别预测不同的分类结果。先看第一个例子hθ(x)=g(θ0+θ1X1+θ2X2)，其中θ0 ,θ1 ,θ2分别取-3, 1, 1。则当−3+X1+X2≥0时, y = 1; 则X1+X2=3是一个决策边界，图形表示如下，刚好把图上的两类点区分开来：

例1只是一个线性的决策边界，当hθ(x)更复杂的时候，我们可以得到非线性的决策边界，例如：

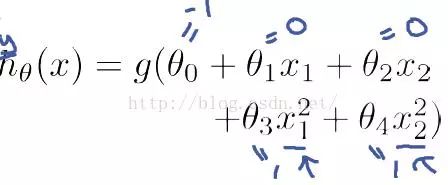
这时当x12+x22≥1时，我们判定y=1，这时的决策边界是一个圆形，如下图所示：

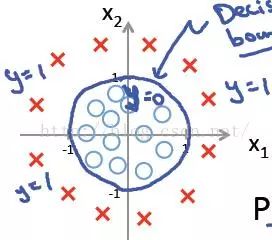
所以我们发现，理论上说，只要我们的hθ(x)设计足够合理，准确的说是g(θTx)中θTx足够复杂，我们能在不同的情形下，拟合出不同的判定边界，从而把不同的样本点分隔开来。

直观地在二维空间理解逻辑回归，是singmoid函数的特征，使得判定的阈值能够映射为平面的一条判定边界，当然随着特征的复杂化，判定边界可能是多种多样的样貌，但是它能够较好地把两类样本点分隔开，解决分类问题。