

一文看懂傅里叶变换知识!!!
描述
一、时域和频域
时域是瞬息万变的,频域是亘古不变的。
傅里叶先是在他那个年代有了一个十分超前的想法,所有波都是不同的幅度、频率、相位的正弦波组成的,这在当时,包括他的老师都是持反对意见的,理由很简单,你拿线条圆滑的正弦给我组个线条笔直的方波、三角波看看。
然后傅里叶就整了一个傅里叶变换(以下简称FT)出来,证明方波、三角波至少在数学上就是可以用正弦波组合出来,但是当时没有什么物理上的证明。
随着欧洲工业革命的兴起,特别是近几十年来图像处理技术的登峰造极,现在人们早已经不是去证明其真伪,而是借助这把工具来处理形形色色的应用。这么说吧,FT是处理“波”的,而“波”就是一种信号,所以只要涉及到信号这个层面的内容,FT都可以发挥一定的作用。
FT的本质,是时域的周期性连续信号可以在频域上由不同频率和幅度的正弦波的叠加,我们通过下面这张图来说明一下这个问题。比如一个方波被不同数量、不同频率和不同幅度多叠加后对比可以让我们很初步的认识FT。
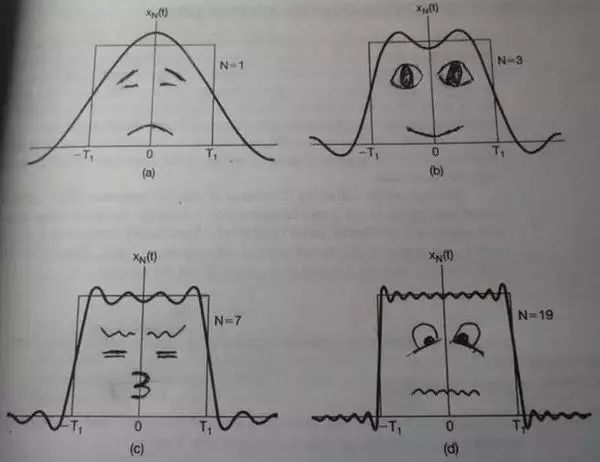
不同数量叠加后的效果
第一幅图是一个郁闷的正弦波cos(x);
第二幅图是2个卖萌的正弦波的叠加cos(x)+a.cos(3x);
第三幅图是4个发春的正弦波的叠加;
第四幅图是10个便秘的正弦波的叠加。
不是看到了正弦波数量越多,叠加后的波形越来越符合原方波。那么,如果是无限个正弦波进行叠加呢?
二、欧拉公式
直截了当,不管你记得不记得,我先把欧拉公式摆出来吧。
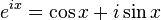
虚数i这个概念大家在高中就接触过,但那时我们只知道它是-1的平方根,可是它真正的意义是什么呢?
这里有一条数轴,在数轴上有一个红色的线段,它的长度是1。当它乘以3的时候,它的长度发生了变化,变成了蓝色的线段,而当它乘以-1的时候,就变成了绿色的线段,或者说线段在数轴上围绕原点旋转了180度。
我们知道乘-1其实就是乘了两次i使线段旋转了180度,那么乘一次i呢——答案很简单—旋转了90度。
同时,我们获得了一个垂直的虚数轴。实数轴与虚数轴共同构成了一个复数的平面,也称复平面。这样我们就了解到,乘虚数i的一个功能—旋转。
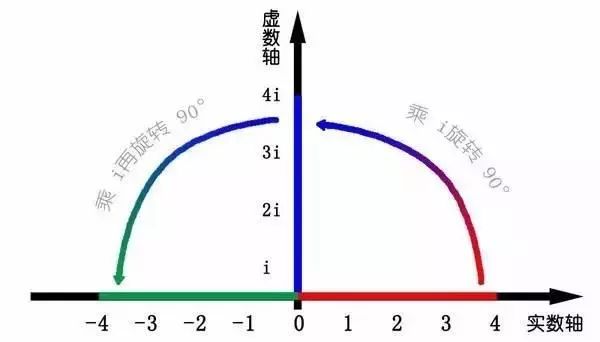
实数轴和虚数轴
在学习复变函数之前,我们接触到都是实数;复变函数是向虚数进行了延伸,而欧拉公式是这种延伸的桥梁。不单单是FT,它还在很多领域发挥了关键的作用。
三、FT的本质
上面提到了FT的本质,下面这样图就是把时域和频域放在一个大坐标系里进行说明。那么,FT的公式,就是变成了求得这些不同幅度的正弦的幅值。因为它们的频率是基于原时域波形而有规律的变化,所以频率是已知的。同时还有个为了符合原波形的幅度而引出的直流分量。求得了这些,也就是完成了整个的FT。

FT的本质
FT公式:
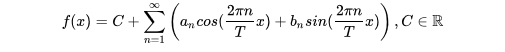
其中C就是上面提到的直流分量,an和bn就是不同频率的正弦的幅度。
最后需要说明的是,FT是DFT和FFT的基础,只要先把FT的本质掌握了,后面两者只是对FT的具体应用和实现的形式。
-
经典傅里叶变换与快速傅里叶变换的区别2024-11-14 1993
-
一文道破傅里叶变换的本质,优缺点一目了然2024-03-12 1005
-
什么是傅里叶变换和逆变换?为什么要用傅里叶变换?2024-01-11 6199
-
傅里叶变换的定义 傅里叶变换的意义2023-11-30 3915
-
傅里叶变换基本性质 傅里叶变换本质 傅里叶变换的应用2023-09-07 7620
-
有关傅里叶变换的相关知识2021-10-08 2680
-
DSP变换运算-傅里叶变换2021-08-03 2550
-
二傅里叶变换是什么?如何求傅里叶变换?2021-05-08 2460
-
小波变换比傅里叶变换好在哪里_小波变换与傅里叶变换详解2018-01-13 16740
-
【安富莱——DSP教程】第23章 傅里叶变换2015-06-25 7133
-
什么是傅里叶变换2007-11-29 10300
全部0条评论

快来发表一下你的评论吧 !

