基于RO电路变化PUF的FPGA实现

现代密码协议规定只有授权参与者才可以获得密钥和访问信息的权限。然而，通过侵入系统泄露密码的方法层出不穷，给现代信息安全造成严重的威胁。对此问题，PUF不可克隆的优点，为信息安全提供了进一步的保障。例如：RO PUF、Arbiter PUF、SRAM PUF。通过把物理信息集成到电路设计从而实现PUF的设计，与现有RO PUF相比，PISO移位寄存器的运用减少了更多的硬件资源。由4位激励能够产生16位随机响应，大大增加了激励响应对的数目，而且通过FPGA测得内部汉明距离是符合要求的。

引言

加密是信息安全的一个分支，其中包括数据安全性、数据完整性和安全认证机制。加密技术的使用使得通信安全有了保障。发送方终端通过密钥对数据进行加密，在接收终端以相同的密钥或派生密钥解密信息。加密体制依据解密与加密所用秘钥是否相同，将其划分为对称和非对称密码两种体制。在对称密码体制中，加密密钥和解密密钥是一样的。而非对称密码体制中，加密密钥和解密密钥是分开的，不相同。加密的密钥不应该受到环境的影响，应该是随机的、可靠的以及抗侧信道攻击的。 一种基于PUF的密钥产生机制如图1所示。

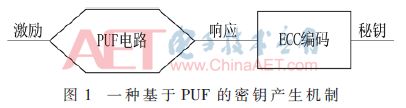
经典线性反馈移位寄存器用于随机数生成。伪噪声随机数字发生器（PN-RNG）是利用初始种子产生随机数序列的。由于有一组共同的初始种子，伪噪声随机数发生器（PN-RNG)产生的随机序列并不随机，如果有人存储这些序列，根据序列之间的相关性，即PN-RNG在产生最大值之后开始产生相同的序列，对手可以预测到下一个序列[1]。加密密钥是数据安全的关键，秘钥一定是可信可靠的随机数。真正可靠的密码体系应该是：即便破译者可以加密任何的明文，也没法破译密文。一般地，如果仅根据密文就可以推算出明文或密钥，则称这个密码体制是可破译的。基尔霍夫原则指出“一个密码体制是安全的，其总的前提就是假设密码分析者已经知道了密码体制的算法，体制的安全性仅依赖于密钥的保密”。现在的人喜欢依赖手机进行电子交易，所以信息安全得到了更多的关注。硅密钥因为具有不可克隆的特点而被优选，不可克隆是指：即使用相同的材料也不能制造出2个性能相同的设备。2001年Srini Devadas(麻省理工学院CSAIL)提出了用物理不可克隆函数(PUF)来生成密钥的IC。PUF是一种基于器件和工艺偏差的体系。从PUF系统可以产生不可预测的随机数，不过PUF产生的随机数必须经过编码才能获取想要的密钥。PUF电路利用器件的特定属性生成随机数，这些属性是无法克隆的，并且很难预测。根据半导体的任何可变属性都可以用来构建PUF。延迟、频率和SRAM上电初值的PUF，已在早期研究工作中有所研究，这些PUF[3]都反应了制造设备的随机性变化。PUF电路必须能够产生大量的激励响应对。对于每个激励响应都应该独特而不可预测。对于不同的PUF，同样的激励生成的PUF响应应该都是不同的。PUF的性能可以用唯一性、可靠性和稳定性衡量。唯一性一般用内部汉明距离表示，理想值μ=0%。它代表了对于不同的PUF给予相同的激励条件，得到响应之间的差异性。文献[3]中展示了唯一性，用这种特性来识别电路。可靠性一般用片间汉明距离表示，理想情况下μ=0%。它代表对于同一个PUF，给予两个相同的激励，得到响应之间的差异性。稳定性表示响应受温度、老化效应、电源电压、噪声等环境的影响。理想的响应应该是独立于这些因素的[4]。

1 典型RO-PUF

RO PUF是PUF中常见的应用之一，其基本结构单元是环形振荡器(Ring-Oscillator，RO)。RO的构成如图2所示。

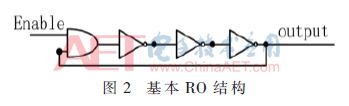
环形震荡PUF是一个将激励映射到响应的频率变化函数。RO PUF是由于工艺偏差而产生的变化频率来生成随机数的。图3给出了N个环振荡器产生的不同频率f1，f2，…fn，这里2个并行的多路复用器的选择取决于输入激励。两个多路复用器选定两个不同的频率 ，它们分别作为n位计数器的时钟输入。然后，两个计数器对选定的两个频率开始计数。如果Q1>Q2响应为1，否则输出响应为0。

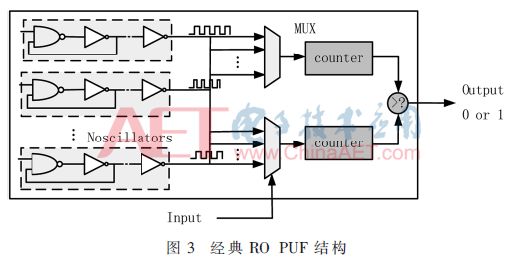
2 本文提出的方案

本设计是利用不同数量的环形振荡器而不是基于工艺偏差用相同数量的环形振荡器来获得变化的频率。图4所示的电路图有3个工作模块：(1)产生不同频率的环形振荡器，分别用不同阶数的RO震荡环产生5个不同的震荡频率；(2)映射阶段，它是一个D触发器的级联，将环形振荡器产生的任意两个频率作为D触发器的数据输入和时钟输入，输出是一个采样频率。本设计中将F1、F2、F3、F4作为D触发器的数据输入，其对应的时钟输入分别为F2、F3、F4、F5；(3)选择电路，基于多路复用器的选择电路，根据激励输入选择4个时钟脉冲，并作为计数器的时钟脉冲。在计数某个确定时间后，计数器值锁存到PISO移位寄存器，在移位寄存器的每个时钟有效边沿产生1位响应，重复16次，获得16位响应。图4电路代表激励响应对产生的方案，4位激励被映射到16位响应，这个PUF是变化频率和频率映射阶段的随机函数。提出的电路结构在Virtex5上得到验证。

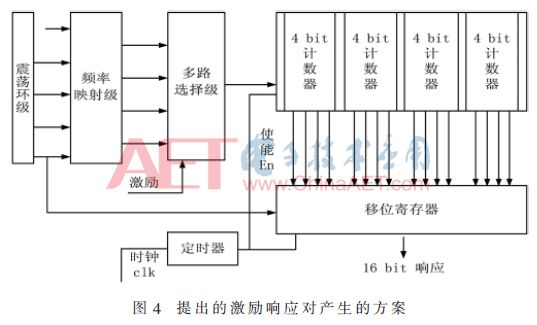
2.1 环形振荡器

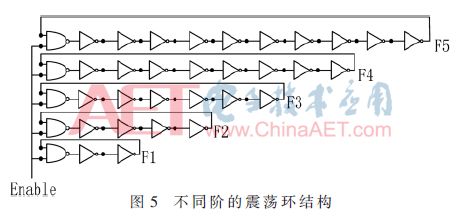
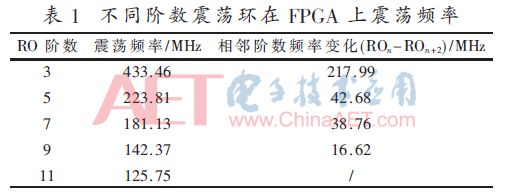
电路由5个具有奇数个反相器的环形振荡器组成，目的是获得不同的变化频率。每个RO由图5所示的nand门的输入Enable控制，使能Enable信号为高开始振荡。环形振荡器由奇数个反相器构成，其频率取决于反相器的阶数，对于N阶环形振荡器，振荡频率为：Fosc=1/τpd=1/(2Nτp)，其中τpd=τphl+τplh，N为反向器的阶数[5]。从表达式发现，随着反相器阶数的增加，频率下降，频率也彼此接近。表1显示震荡频率随着反相器数量的增加而发生变化。

2.2 映射阶段

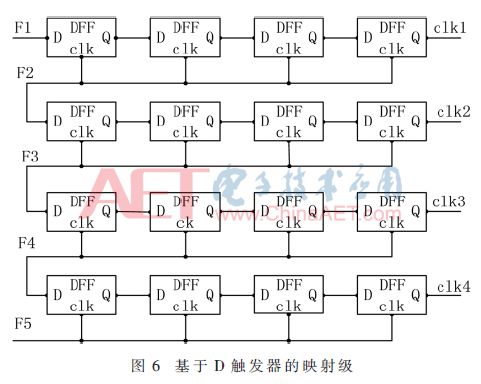
它是由4级D触发器级联，D触发器将两个频率中一个作为数据输入，另一个作为时钟输入，获得一个采样输出，图6所示的第一行4级D触发器数据输入端接F1，时钟输入接F2，采样输出记为CLK1。在本设计中使用时钟上升沿触发有效; 如果D触发器时钟上升沿比数据上升沿提前，输出保持上次结果不变，如果时钟上升沿比数据上升沿落后，则输出与触发器数据端输入端一样。同理，第二行、第三行、第四行4级级联的D触发器产生CLK2、CLK3、CLK4，产生的4个时钟脉冲信号将用于下一级的频率比较阶段。由于振荡器频率不同，它们的边缘到达时间是不可预测的，这就增加了更多的随机性到PUF电路。在数据和时钟边缘同时到达的情况下将导致亚稳态，在下一个边沿时钟脉冲产生完全不可预测的电路输出（高或低）。并且本文采用的是慢时钟采快时钟，根据麦奎斯特采样定理，肯定会有信号遗漏，但是我们并不是想要最后得到完整的数据信号，仅仅是利用丢失信号的不确定性来增加PUF电路的随机性。

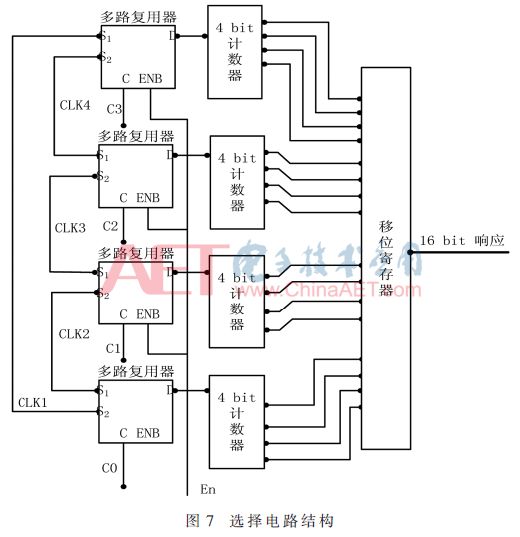
2.3 选择电路

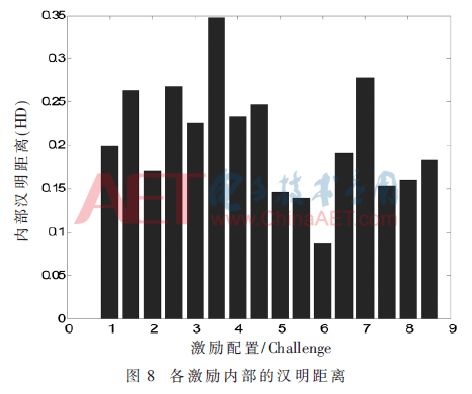
图7所示电路是多路复用器构成的选择电路。时钟上升沿到来计数器向上计数。在计数某个确定时间后，计数器值锁存到PISO移位寄存器，在移位寄存器的每个时钟有效边沿产生1位响应，重复16次，获得16位响应。图8给出了16个激励的内部汉明距离，这几乎是理想的值。本文提出的PUF结构与现有的RO PUF相比，需要更少的硬件资源。图3显示了2个计数器产生1位响应的RO结构。要有16位响应，它需要32个计数器和16个比较器并行工作。并且提出的PUF结构相对于RO PUF在计数阶段消除了硬件复杂性，并从单个计数器和PISO移位寄存器直接产生16位响应。

本文提出了一种新颖的基于硬件的产生激励响应对的RO PUF结构，其结合电路变化而不是工艺偏差。运用频率映射与PUF结合的策略产生随机性响应，响应的内部汉明距离几乎达到理想值。PUF的早期设计中2个计数器产生1位响应，当前设计中用相同位数的计数器产生16位响应。在接下来的研究中计数器和PISO移位寄存器的大小可以增强到255位，为AES加密算法生成128位密钥。

3 实验与分析

本文将上述方案在FPGA平台上进行实验测试，实验开发板：Xilinx Virtex5，开发软件：集成开发环境ISE，仿真工具Modelsim，测试和分析工具ChipScope；开发语言：Verilog HDL。经过XST综合后的FPGA配置文件下载到开发板上，时钟周期是50 ns，定时器定时时间为0.512 μs。用ChipScope 软件抓取输入激励与其对应输出响应的波形图。通过ChipScope 导出的波形图，解析出激励-响应对。在测试过程中，对电路进行了50 次测试，每次测试能够得到16个激励-响应对，对同一个激励产生的50个响应计算内部汉明距离，结果表明，该电路对于同一激励的响应内部汉明距离最大为0.277 8，最小可以达到0.080 0，大部分分布在0.200 0左右，文献[14]中测得的内部汉明距离9次达到0.310 0，6次达到0.190 0，1次达到0.250 0，所以比较文献[14]，本文设计的PUF较优，该设计满足PUF函数的相关要求。

4 结论

本文的设计是通过把物理信息集成到电路设计从而实现PUF的设计，与现有RO PUF相比，PISO位寄存器的运用减少了更多的硬件资源。由4位激励能够产生16位随机响应，大大增加了激励响应对的数目，也即增加了ID的数量，安全性得到提高。并且经由FPGA验证本文改良后的RO PUF具有更高的“片内稳定性”。环境温度、供电电压是影响片内稳定性的重要因素，确保ID不随温度、电压发生变化，并且精确可重复生成是未来研究的方向。